Land sat image processing by NEC. Acos-4.

Land sat image processing by NEC. Acos-4

Kesol Petchsuwan Ph.D.
Pairash Thajchayapong Ph.D.
Kanchit Maitree M.Eng
Faculty of Engineering
King Mongkut’s Institute of Technology
Ladkrabang Campus
Ladkrabang, Bangkok,
Thailand.

Abstract

A research is now undergoing to process a LANDSAT CCT file using the newly-installed NEC ACOS –4 at KMIT. The basic process includes reformatting, grey mapping and recognition. It is also investigated the possibility of image enhancement using techniques such as orthogonal transform, 2-D digital filtering etc. Data compression is shown here as one of the results.

1. Introduction

For a given scene, one frame of a 4-band LANDSAT imagery consists of four images. One image is represented by a 2340 x 3248 array of pixels. If each pixel is a 6-bit binary word, then the number of bits required to store one frame is approximately (2340) (3248) (6) (4) = 180x106. More over if 30 frames are collected per day, it sum up to approximately 5,500x106 bits per day to be stored. Hence, reproduction techniques to reduce this enormous number of bits would economically save the amount of magnetic tapes required to keep the LANDSAT data.

Problem please see the equation

2. Optimum Transforms

2.1 One –Dimensional Transforms

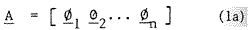
Let A be the kernel of an orthogonal transform which

Where ø1 are n-vectors. Also the vector basic are assumed to be orthonormal i.e.

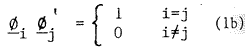
for each data vector X of a given class of data vectors, where X [ x1x2 -- xn] , we find its transform version Y, where Y = [y1 y2 -- yn]

from

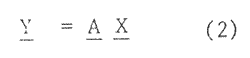
Since A A' = 1, hence

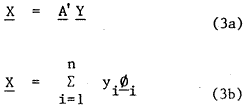
if a subset { y1 y2 -- ym} of Y is retained to give an estimate X of X i.e,

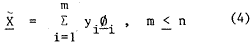
then the error arises from such truncation is

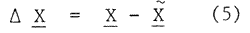
The øi which provides a minimum-mean square error of

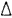X has been proved to be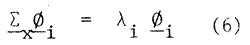

where

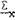is the covariance matrix of

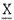. It indicates that

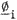is the eigenvector of

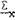and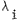

is the corresponding eigenvalue.The kernel A consisting of such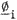

is known as the Karhunen-Loeve transform (KIT) or Hotelling transform.

If y_i is coded as a b-bit binary and m out of n components of Y are retained, we obtain a reduction ratio of n/m bit/component . Although KLT is the optimum transform, other sub-optimum transform such as discrete cosine Transform (DST), Walsh-Hadamard transform (WHT) etc. are preferred in practice as the latter prove to be computationally much more efficient.

1.2 Two –Dimensional Transforms

For an (nxn) image matrix

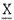its transform (nxn) matrix

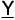is given by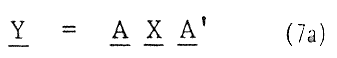

and also the inverse transfrom by

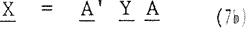
All transforms mentioned in the one-dimensional transform case are applicable to two-dimensional transform of image matrix.

2. Image Data Compression

For a given image of dimension NxN, it is divided into subimages of size nxn where n< N as shown in Fig. 1

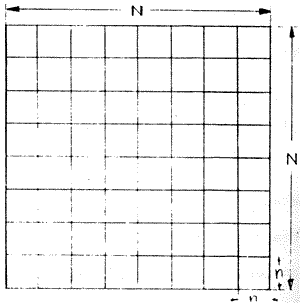
Fig. 1 An NxN image divided ito nxn subimages

The data compession is performed by the following steps

determine the two-dimensional transform

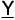of each subimage

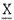retain m components of

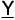with largest variances

determine the inverse transform to obtain
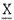
The bit reduction factor is defined by

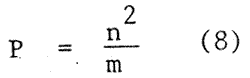
Fig. 2 show results of testing data. Fig. 3 illustrates the data compression of a Landsat 64 x 64, using Walsh transform

Fig 2 (a) Saturn 5 bits/pixel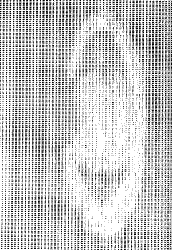
Fig 2 (b) Saturn 2.5 bits/pixel

4.Conclusion

It has been demonstrated how to perform data reduction using transform techniques. Hadamard transform was chosen as an example due to its computational efficiency. Further investigation should be made for other transforms. The main applications of data reduction will be the economical use of storages or for data transmission of , for example, LANDSAT image data.

Acknowledgments

The authors would like to thank National Research Council of Thailand for Lending the LANDSAT CCT tapes. Also, we wish to thank Mr. Vorawoot Suwatanapankul and Mr. Chaiwat Yawwapapong for their useful helps.

References
1. P.A.Wintz, “Transform Picture Coding”, Proc IEEE, vol. 60, pp.809-820 July 1972
2. A. Habibi and G.S. Robinson,” A Survey of Digital Picture Coding,” IEEE Computer, vol 17., pp. 22-34, May 1974.