An Analysis of Training Sets for Supervised Classification of Multispectral Remote Sensing Data.

An Analysis of Training Sets for Supervised Classification of Multispectral Remote Sensing Data.

Dr. Kaew Nual chawee
Assistant Professor or Computing and Remote Sensing,
Regional Computer Center and Asian Regional Remote Sensing Training Center,
Asian Institute of Technology, P.O. Box 2754,

Dr. Lee D. Miller
Professor of Forestry and Remote Sensing,
Remote Sensing Center, Texas A&M University,
College Station,
Texas 77843, USA

Dr. Sathit Wacharakitti
Assistant Professor of Forestry,
Faculty of Forestry,
Kasetsart University,
Bangkhen, Bangkon 9, Thailand

Abstract

A forest land use/land cover classification was undertaken using LANDSAT MSS data together with cellularized digitized landscape data of the same study area. Stepwise linear discriminant analysis in LANDSAT Mapping System (LMS) developed at Colorado State University was selected for the classification of the combination of LANDSAT/Landscape variables. This classifier provides flexibility of specifying two choices of a priori probability of occurrence of the land covers being classified , i.e. proportional a priori probability and equal a priori probability. There types of training sets or prototype selections were tested in the classification and they are:

Conventional rectangular (areal) training sets.
Modified rectangular training sets which separate the rectangular areas into two classes representing sunlit and opposite orientations called aspects, and
Systematic single point grid type taining sets.

The rectangular training sets consistently yields higher training set accuracies using the discriminant analysis routine. The grid or single cell sampled training sets yielded lower training set accuracy but yielded higher map verified accuracy.

This study is part of a major research program conducted by the authors at Colorado State University. Fort Collins, Colorado, USA, during the year 1972 through 1978.

The proportional a priori probability yielded the higher classification accuracies but tend to over and under classify those land cover types with larger and smaller populations respectively. Equal a priori probability gave lower over all accuracies but yielded a better display of the spatial distributions of the cover types.

Introduction

When one considers current predictions concerning population growth and compare them to the existing conditions for our natural resources, it becomes obvious that a great need exists for obtaining accurate up-to –date information concerning our resource base. Only by providing our resource managers with the type of information that they require can we hope that they will be able to carry out their jobs efficiently and effectively. Remote sensing is a tool which shows promise for the solution to several problem areas of application and management of our natural resources.

The capability for acquiring and utilizing multispectral data was greatly increased when LANDSAT –I was launched in 1972. two of the most significant characteristics of the LANDSAT data are its wide area and repetitive coverage. These attributes together with machine-assisted data analysis and classification methods have been used for many natural resource surveys in which LANDSAT data is used identify and estimate the areal extent of crops (MacDonald, et al. 1975).

The digital processing and analysis of data from LANDSAT or other multispectral Scanner system (MSS) normally involves several major steps which include but not necessarily limited to, (Hoffer and Fleming, 1978):

Data reformating and preprocessing,
Development of training statistics,
Computer classification results, and
Display and tabulation of information (For resource management and /or other purposes).

It is the purpose of this study to look into the development of training statistics of the samples selected as representative of the whole area. The essence of computer-assisted analysis of multispectral data involves “training” the computer to recognize a paraticular combination of number representing the reflectance in each of several wavelength bands from a particular material or cover type of interest. After a good set of training statistics has been developed, the computer is programmed to classify the reflectance values for every resolution element for which reflectance measurements were obtained by the multispectral scanner system.

The real key to an accurate computer classification of the data lies in the definition of a set of training statistics which are truly representative of the spectral characteristics of the various earth surface feature present in the multispectral data. This leads to the need for the analyst of develop a thorough understanding of the spectral characteristics of earth surface features. Without an in-depth understanding of the material characteristics of the material characteristics of the various materials with which he is involved, the analyst will not be able to utilize in classifying MSS data.

There are three different approaches in training computer to recognize surface features or “training samples”. The first approach is referred to as the “Supervised technique”, and involves use of the system of X-Y coordinates to designate to the computer system the locations in the data of known earth surface features that have informational value. For instance, at a particular coordinate in the data is a field of rice, at another is a field of corn, and another a field of sugar cane, etc. the supervised technique or “training sample” approach has been used quite effectively or agricultural mapping of large and flat area (LARS Staff, 1968; Bauer and Cipra, 1973).

A second approach to training the computer system involves the “clustering” technique which is also referred to as the “non-supervised” technique. In this approach the analyst simply designates the number of spectrally distinct classes into which the data to be classified should be devided. The computer is programmed to classify the data into the designated resolution elements in the data belongs to which spectral class and then printout a map indicating which resolution elements in the data belong to which spectral class. The analyst then simply relates this classification output map to known surface observation data, and determines which materials actually are represented by each of the different spectral classes. With this approach the analyst can not determine knowledgeably in advance the number of spectral classes present. Of ten time, one finds that the classes of most interest have subtle spectral differences, whereas many of the other classes present in the data may be easily separated spectrally but are of little information value or interest to the user.

A new and so-called “modified clustering” approach has recently been developed by LARS and has proven to be extremely effective in working with satellite multispectral data (Fleming, et al, 1975). In this method, several small blocks of data are defined, each of which contains several cover types. Each area or data block is first clustered separately, and the spectral classes for all cluster areas are subsequently combined. In essence, the modified cluster approach entails discovering the natural groupings present in the data, and then correlating the resultant spectral classes (crop species, cover types, vegetative conditions, etc.). This technique is particularly useful in wildland areas, or where the fields are small, or where the cover types and spectral classes are complex. In the most cases, less than one per cent of the data involved in the analysis is used for training phase (Hoffer, 1979).

Study Objectives

This study concerns primarily with superwised training approach with three kinds of training set selections and two a priori probabilities of occurrence. The availability of the software package and collateral data permitted only supervised approach.

General objectives are to apply supervised training approach to area under investigation and to determine classification accuracy of each training set approach selected for the classification with two different a priori probabilities of occurrence as weighting factors. Specific objective of the study include the following:

To devise procedure for selection of training area to effect represent spectral reflectance characteristics of particular types.
To utilize LANDSAT MSS band/ratios and landscape data planes the area as input variables for computer classification.
To compare training sample classification accuracies and to classify the whole study site using training statistics obtain from each training procedure selected under I) above, and
To determine if LANDSAT MSS band/ratios and landscape data contribute to classification accuracy.

Materials and Methods Aproach

1 Test Site Description

The study site called “Nikon Doi Chiangdao” (a Hill Tribes Settler was selected to represent a tropical forest site of this study. It is situated in Chiangdao district, Chaingmai Province in Northern Thailand between latitude 190 201 N and longitude 980 451 and 980 59 (Figure 1). This general area can be related to the Golden Triangle because of the nearness to the corner of the intersection of China, Bur Laos, and Thailand where hill tribes people engage in slash and burn agricultural practice for their subsistence. It represents mountatinous are which was originally heavily forested but has been rapidly cleared for shifting cultivation of opium, dry-land rice, tea, and other crash crop. It is typical of a large portion of the world’s tropical forests where and-burn agriculture is out of balance with regrowth and the mountains and watershed are being rapidly denuded.

The climate of the study area is alternate wet-dry tropical under influence of the southwest monsoon. The rainy season beings from May to November. The cold-dry season lasts from October to February, the hot-season from March to April. The Mean daily temperature is 21°C to 27°C. The mean relative humidity is about 82 per cent.

2 Input Variables and Reference Data

2.1 LANDSAT MSS band/ratio Data

The primary data input for this study was obtained from the LANDSAT –I pass over the study site on January 27, 1973 with specific Scene ID number of 188-03224. This specific scene was selected because it was the only scene with cloud free and was taken within weeks of the airphotos taken in December 1972. This closest match the most recent airphoto coverage and the earliest LANDSAT coverage provide a source of known, coincident ground cover which could be use for both training and verifying the LANDSAT classification tests.

This LANDSAT data plane was geometrically corrected and resar pled to one hectare resolution cells to prepare for overlaying with landscape data planes of the area. Then transformation of this data was performed by rationing of the four bands which resulted in six band ratios in addition to the original four MSS bands. The 10 MSS band ratios consists of MSS bands 4,5,6 and 7 plus ratios of 5/4, 6/4, 7/4, 6/5, 7/5, and 7/6.

Figure 1 Locatio of the study site.

The study site is located in Chiangmai Province of Northern Thailand near the area of the intersection of China, Burma, Laos and Thailand boarders. It is representative of the general area which is mountainous and was originally heavily forested but has been rapidly cleared for shifting cultivation of various agricultural practices.

2.2 Landscape Data Planes

The study site was enclosed in a rectangle of 432 square kilometers (24 km E-W and 18 km N-S) and was cellularized with a resolution of one hectare yielding 43, 200 cells. The actual study area bounded by the rectangle consisted of an area of 293 Km2 or 29, 300 square cells of 1 ha resolution. The landscape data planes that were used for entering into classification scheme consisted of minimum distances from point and line features such as housing and transportation; and physiographic data planes such as elevation, slope, and aspect. Each of these data planes has common area of 29, 300 ha each with 1 ha resolution. Construction of these data planes has been presented elsewhere (Nualchawee, Miller, and Tom, 1979).

These landscape data plane were in agreement in cell size, total number of cell, and in registration with the 10 MSS band/ratios of the LANDSAT imagery prepared earlier. They were then merged together in a composite LANDSAT/landscape data file using a computer module of the LMS software package. This yielded a file containing multivariables registered cell-to-cell for the rectangular area of 43, 200 cells and with a common irregular data area of 29, 300 cells.

2.3 Reference Data Plane

reference data used for this study was obtained from forest land cover type map derived from aerial photointerpretation of 1972(Wacharakitti, Miller, and Tom, 1975). This forest land use map was closest to the time the LANDSAT data of 29 January 1973 was collected. The reference data consisted of 9 land cover classes as follows:

Hill evergreen forest
Mixed deciduous forest with teak
Dry dipterocarp forest
Dry evergreen forest
Swidden area (Shifting cultivation)
Irrigated rice fields
Tea plantation, and
Teak planta

3. Selection and Testing of Training Areas for Multivariate classification.
A feature selection with multispectral data can be done using training sets or prototypes. A training sample to represent a land cover type is formed by grouping together a small, representative number of those cells in the image files that are alike and represent a know land use or land cover class. Likeness of the cell assembled together to represent one class is specified by statistical similarity in the radiance values record for those cells for a particular variable. Thus a training set is a subsample whose identification is known to some acceptable level of accuracy and should be representative of each of the land use/land cover classes to be investigated. The training set is used to generate subpopulation statistics to efficiently implement decision rules in the classification approach tested in this study.

Three kinds of training set selections were used in features selection for this study : rectangular training area, rectangular training areas in sun and shade (aspect training areas), and grid sample training areas. All three training sets were carefully selected to represent specific land cover classes. The multivariate data consisted of the 27 January LANDSAT MSS band/ratios with four topographic features of slope, aspect, elevation, drainage and three cultural feature data planes of minimum distances to temporary housing, to permanent housing, and to roads and trails. Specific combinations of these 17 LANDSAT/1 landscape variables were selectively chosen to enter into the features extraction procedures and subsequently into the machine classification for optimal ordering by the stepwise linear discriminant analysis algorithm. Eight land cover categories were used in the features extraction and machine classification and the ninth cover type of teak plantation was omitted as it occupied only 40 hectares in the entire study site. For all training set classification five sets of variables were used in the process. The sets of variables test in the separate classification computation runs were:

2 variables (MSS bands 5 and 7)
4 variables (all four LANDSAT MSS band)
10 variables (the 4 above plus the 6 ratio bands)
14 variables (the 10 above plus topographic slope, aspect, elevation, and minimum distance to drainage) ; and
17 variables (the 14 above plus minimum distance to permanent housing, minimum distance to temporary housing, and minimum distance to read and trails).

Training set accuracy is a measure of how well a selected training set represent the specified known land cover classes (es) through the training set classification algorithm. Training set accuracy is defined here as the number of training set cells which are correctly classified to the proper class(es) divided by the total number of cells in the training set input to the text classification representing the class (es). Therefore, training set accuracy expressed as a percentage is given as:

(100 x correctly classified map cells) / (total map cells classified)

Resultes and discussion

1 Test Classification for Grid Training Sets

The first training set approach selected to test features extraction for supervised classification was a systematic sampling of cells selected by their grid position within the entire area of the study site. This grid sample point training set was formed by resampling every third row and third column of cells in the 1972 land cover data plane which serves as ground truth for this analysis. This sampled data points were identified by the land cover codes given in the original 1972 land cover data plane. The one-ninth data cells sampled by this grid approach were reground into eight similar training samples representing the land cover categories of the study site. The population of the training samples selected in this fashion were proportional to the relative occurrence of the land cover types in the study site, i.e., the larger the areas of the land cover types, the more frequent they were sampled and vise versa. The 3, 158 data points statistically sampled in this fashion represents all the multispectral variability induced by the natural conditions of the land cover in the entire area to be mapped.

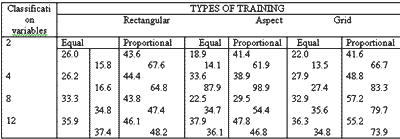
The training set accuracy obtained for grid sample are presented in Table 1 according to variable set selected . the corresponding accuracy curves are presented in Figure 2. since the one-third by one-third rectilinear point training set sample of 3, 158 cells constituted a representative statistical sample of the cells in the final map to be prepared, the training set accuracy in this grid approach also represent verification accuracy, and further test or verification would not be required.

Table 1. Land sat/landscape variables selected using grid sampled trading set to classify themselves.

The landscape model employed in this classification contained the 4 MSS bands and 6 band ratios for the 27 January 1973 LANDSAT image together with the 4 physiographic data planes and 3 of December 1972 cultural features data planes. All variables were selected in a free, optimal order by stepwise linear discriminant analysis (Figure 2), Training set accuracies expressed hare can also be taken as equal to verification accuracies for these training sets.M.D = Minimum Distance.

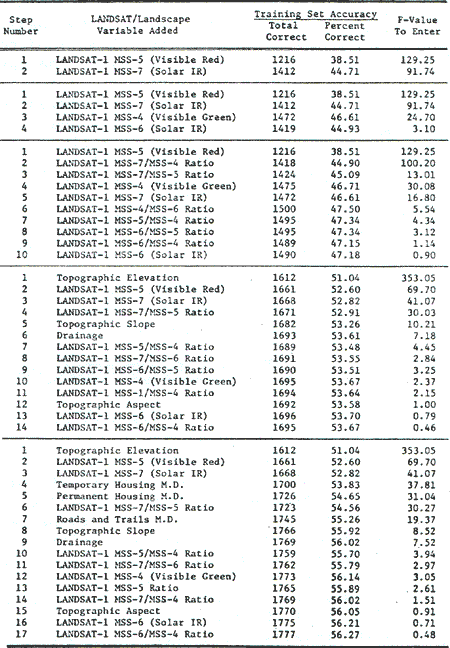
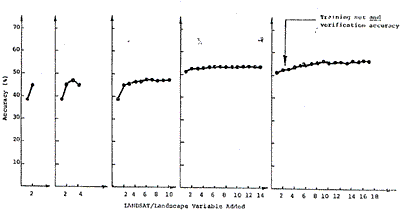
Figure 2. Accuracies achieved using grid sampled training sets to Classify themselves

The grid training sets represent a sample of 3, 158 data points consisting of every third row and column of the study site which has been regrouped into 8 populations representing the desired 8 land cover types. They were selected to represent each of the covers types for various combinations of 17 LANDSAT/landscape variables (Table 1) and were used to form classification matrices with stepwise linear discriminant analysis. The classifier and matrices were then applied back to the grid sampled points to determine how accurately they classify their own original populations (i.e. training set accuracy). However, since the grid derived data is a sample of the map to be classified these accuracies represent the final map accuracies had the total population of points in the area been classified and checked (i..e. 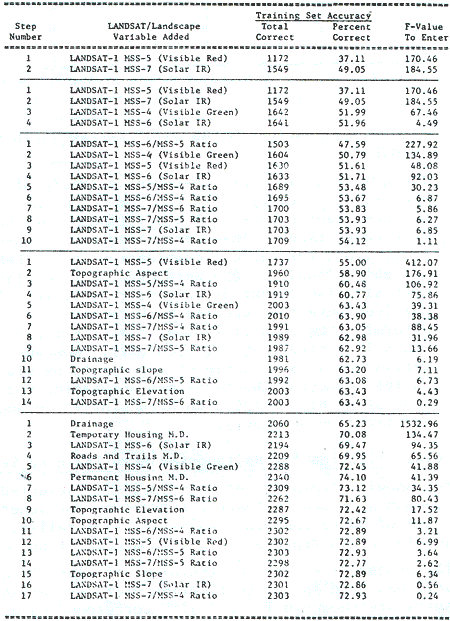verification accuracy).2 Test Classification for Rectangular Area Training Sets

The rectangular training set were carefully selected to test the use of this very common approach in feature extraction for supervised classification. A total of 40 rectangular training sets totaling 3, 158 one hectare cells were selected to represent eight land cover types of the study site.

Similar procedure to that of training set classification for grid training sets was used for classification of these rectangular area training sets. Results are shown in Table 2 with corresponding accuracy diagram in Figure 3 which follows.

3 Test Classification for Rectangular Area Training Set in Sun and Shade (Aspect Training set)

These aspect training sets were selected as supplements to the rectangular training sets that they have just been described. Classification of forest.

Table 2. Land sat /landscape variables selected using rectangular training sets to classify themselves

The landscape model employed in this classification contained the 4 MSS bands and 6 band ratios for the 27 January 1973 LANDSAT image together with the 4 physiographic data planes and 3 of December 1972 cultural features data planes. All variables were selected in a free, optimal order by stepwise linear discriminant analysis (Figure 3). Applying the same classifier, matrices and all 17 variables to the 3, 158 grid sampled data points correctly classified 1, 439 cells for a verification accuracy of 45.1%.M.D = Minimum Distance

cover types in mountains terrain such as this site are influenced by terrain induced variation in radiance (e.g. shadows). Selecting training areas to separately represent each class sought in both sun and shade conditions has been proposed as approach to ameliorate these effects and to improve classification accuracy when the sun and shade classes are lumped----------------------------------------------- after classification. The selection of the rectangular training ------------------------------ in the prior section was accomplished by overlaying a line ----------------------------- of LANDSAT MSS band of the study site onto the land cover-----------------------------same scale and rectangular areas of relatively uniform gray tone ----------------------------- selected within the area of each specific land cover type.

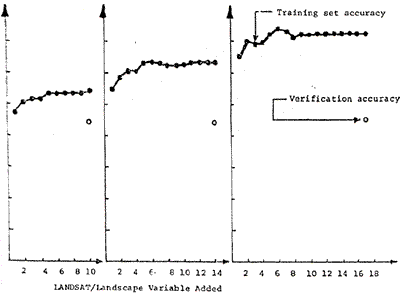
Figure 3. Accuracies achieved using rectangular training sets to classify themselves and a grid sample of the test site.

Rectangular shaped training sets were selected to represent each of the 8 land cover types for various combinations of 17 LANDSAT/landscape variables (Table 3) and were used to form classification matrices with stepwise linear discriminant analysis. The classifier and matrices were then applied back to the rectangular training sets on a step-by-step basis to determine how accurately they classified their own original populations (i.e., training set accuracy). Next the same classifier, matrices, and 17 variables were used to classify a grid sample of 3, 158 data point consisting of every third row and column of the study site. This yields a verification accuracy which closely equals that which would be achieved with this classifier on the total population of points in the area to be mapped.

This approach was also followed in the aspect training set selection except that line printer graymap of the topographic data plane was also used to succivide the eight land cover types into 15 new cover types which were represented by rectangular groups of cells on sun-facing and opposite-facing topographic aspects. The 15 new aspect land cover classes were regrouped back into the eight original land cover classes after classification . The classification accuracy obtained after regrouping was representative of aspect training set accuracy. Once the 15 aspect land cover classes were selected the same testing procedure was followed using the same five combinations of variables mentioned as with the rectangular training sets.

Results of the aspect training set accuracies are shown in Table 3 with the corresponding accuracy curves in Figure 4.

Table 3 Land sat/landscape variables selected using aspect training sets to classify themselves.

The landscape model employed in the classification contained the 4 MSS band and 6 band ratios for the 27 January 1993 LANDSAT image together with the 4 physiographic data planes and 3 of December 1972 cultural feature data planes. All variables were selected in a free, optional order by stepwise linear discriminant analysis (Figure 4). Applying the same classifier, matrices and all 17 variables to the 3, 158 grid sampled data points correctly classified 768 cells for a verification accuracy of 24.3 per cent . M.D. = Minimum Distance.

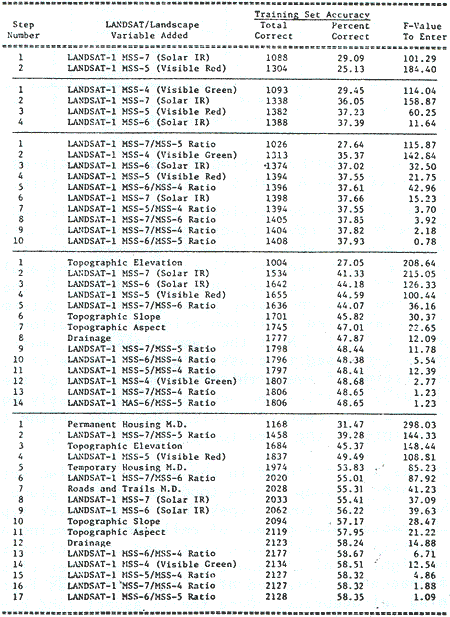
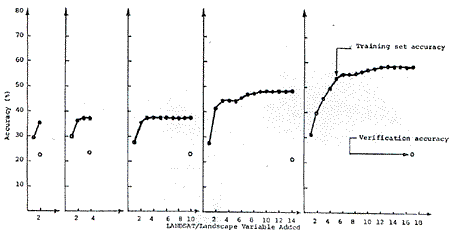
Figure 4. Training set accurate achieved using aspect training sets to classify themselves and a grid sample of the test site.

Rectangular shaped training sets were selected to represent each of 8 land cover types on both sun facing slopes and opposite slopes except for the irrigated rice class which occurs in relatively flat terrain. This yielded 15 “aspect” training sets which represent the cover types sought for various combinations of 17 LANDSAT/landscape variables (Table 4) and were used to form classification matrices with stepwise linear discriminant analysis. The classifier and matrices were then applied back to the “aspect” training sets to test classify the 15 classes and the results regrouped into the 8 original cover types of determine how accurately they classify their own population (i.e., training set accuracy). Next the same classifier, matrices, and 17 variables were used to classify a grid sample of 3, 158 data points consisting of every third row and column of the study site. This yields a verification accuracy which closely equals that which would be achieved with this classifier on the total population of points in the area to be mapped. Intercomparison of the training set and verification accuracies at this point provides insight into the relative value of the three approaches to training a supervised classification algorithm. It also provide further basis for the selection of one of the techniques for use in computing the final classification map to be subsequently presented. Finally it yielded the information needed to select that minimum combination of variables which will minimize computational costs while approaching the optimal accuracies which would be achieved with the use of all available variables. Based on the training set accuracies it was determined that the six ratios of the four LANDSAT MSS bands contributed little to the training set accuracy and they were omitted from further analysis.

Multivariate Map Classification and Map Verification

Actual map classification and verification were undertaken with all three types of training sets to find out how the training set accuracies compare when extended to full map classification and verification accuracy. This will provide a further basis for comparing the approaches and selecting the most accurate one.

The new variable sets used consists of:

2 variables (MSS bands 5 and 7)
4 variables (those above plus MSS bands 4 and 6)
8 variables (those above topographic slope, aspect, elevation, and minimum distance to drainage); and
11 variables (those above plus minimum distance to permanent housing, minimum distance to temporary housing, and minimum distance to roads and trails).

Two assumptions of a priori knowledge of probabilities of occurrence of each forest land cover were tested for their impact on map verification accuracy. They are:

Equal probability of occurrence; and
Proportional probability of occurrence.

The classification results of the various combinations of variables, training set selections, and a priori probability are summarized in Table 4 and their corresponding classification maps for the 11 LANDSAT/landscape variables are presented in Figure 5 and Figure 6 which follow.

(a) Rectangular training set-equal probabilities. Overall verified accuracy = 36.0%	(b) Aspect training set-equal probabilities. Overall verified accuracy = 37.9%
(c ) Gria training set-equal probabilities overall verified accuracy = 36.3%	(d) 1972 Land cover reference map
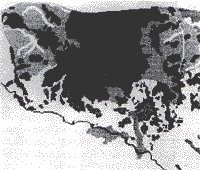	Black = Shifting Cultivation and Tea Medium Gray = Irrigated rice Fields Light Gray = Hill Evergreen Forests White = other Forests
Figure 5 Comparison of land cover classification maps made with ii land sat / landscape variables and each training set and assumption of equal probability of occurrence. The 1972 land cover map is included for reference.
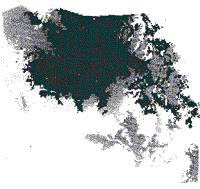(a) Rectangular training set-proportional probabilities. Overall verified accuracy = 46.2%	(b) Aspect training set-proportional probabilities. Overall verified accuracy = 47.8%
(c)Gria training set-equal probabilities. Overall verified accuracy = 46.2%	(d) 1972 Land cover reference map
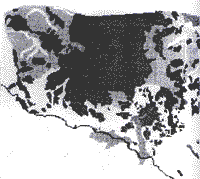	Black = Shifting Cultivation and Tea Medium Gray = Irrigated rice Fields Light Gray = Hill Evergreen Forests White = other Forests
Figure 6 comparison of land cover classifiacation made with ii landsat/landscape varibles and each training set and assumption of proportional probability of occurrence. The 1972 land cover map is included for reference.

Table 4 comparison of map verified classification accuracies derived from various types of training sets and assumptions initial probabilities of occurrence of each cover type.

Total map accuracies were found to generally increase with the addition of new LANDSAT/landscape variables with some exceptions of the aspect training sets (Table 4). The proportional apriori probability approach yielded superior numeric accuracies in all cases by emphasizing those classes with large populations in the study site; such as shifting cultivation. Equal probability, however, yielded classification map with a better spatial relationship with the 1972 land cover map by visual comparison.

Conclusion

It was the purpose of this study to determine the accuracy of computer classification of LANDSAT/landscape variables using three kinds of features extractions or training set selection process, i.e. rectangular area training sets, aspect training sets, and grid training sets. Two assumptions of a priori probability of occurrence of the land cover types, i.e. equal and proportional probabilities were used. Seventeen LANDSAT/landscape variables consisting of ten LANDSAT MSS bands/ratios together with four topographic and three cultural features data planes derived from air-photo interpretation were used in this study. It was determined that the six MSS band ratios contributed very little to the classification accuracy and were dropped from further analysis. Eleven LANDSAT/landscape variables were then used for map classification and verification.

It was found that rectangular training sets achieved the highest training set accuracies in most cases followed by the grid and aspect training sets. However, it was demonstrated that training set accuracy alone does not indicate how well map could be classified using the same training sets. The grid training set achieved the highest map verified classification accuracies of the three with both equal and proportional probabilities.

In conclusion it must be noted that the percentage of correctly mapped points in such a verification as has been employed can not be expected to closely approach 100 percent. The air-photo interpretation maps of land cover upon which the training set extraction was based do not have accuracies close to 100 percent. This initially impacts on the training set identification of the classification results with the known air-photo derived land cover maps. The verification accuracy can only asymptotically approach the accuracy of the air-photo interpretation land cover map with the inclusion of each additional variable or set of variables. Assume, for example that the land cover map derived from air-photos is 70 percent correct. The classification map may be also be 70 percent correct relative to ground conditions. The general causes of error in the unsupervised classification and air-photo interpretation processes are quire dissimilar thus error distributions will spatially mismatch for 70 percent of the occurrences. Thus, verification of the LANDSAT classification map against the air-photo map will produce a 70 percent x 70 percent verification accuracy which is equivalent to 49 percent which approximates the accuracies achieved here with the grid training sets. Where the training set data have been identified from the same air-photo land cover map results and away from the real ground conditions.

Reference

BAUER, M.E. AND J.E. CIPRA, 1973. Identification of Agricultural Crops by Computer: Proceedings of the Symposium on Significant Results Obtained from ERTS-I, Goddard Space Flight Center, pp. 205-212, Greenbelt, Maryland.
FLEMING, M.D., J. BERKEBILE, AND R. HOFFER, 1975. Computer-aided Analysis of LANDSAT-I MSS Data : A Comparison of Three Approaches Including the Modified Clustering Approach, Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, pp. 18-54 to 61. Purdue University, West Lafayette, Indiana. Also available as LARS Information Note 072475
HOFFER, R.M., 1979. Computer-aided Analysis Techniques for Mapping Earth Surface Features, LARS Technical Report 020179.
HOFFER, R.M., AND M.D. FLEMING, 1978. Mapping Vegetative Cover by Computer-aided Analysis of Satellite Data, LARS Technical Report 011178.
LARS STAFF, 1968. Remote Multispectral Sensing in Agricultural, Laboratory for Applications of Remote Sensing, Vol. Research Bulletin No. 844, Agricultural Experimentation Station and Engineering Experiment Station, Purdue University, West Lafayette, Indiana.
MacDOND, R.N., F.G.HALL, AND R.B. ERB, 1975. The Use of LANDSAT Data in a large Area Crop Inventory of Remotely Sensed Data, June 3-5, 1975, Purdue University, West Lafayette, Indiana (IEEE Catalog No. 75 Chapter 1009-0-C), p.p IB, 1-23.
MILLER, L.D., C. TOM, AND K. N. NUALCHAWEE, 1977. Remote Sensing Inputs to Landscape Models which Predict Future Spatial Patterns for Hydrologic Models. U.N. Water Conference, Technical and Scientific Session on Water Resources, Mar del Plata, Argentina (Also NASA/Goddard Space Flight Centre, Rep. X-923-77-115, Greenbelt, Maryland).
NUALCHAWEE, K., L.D. MILLER, AND C. TOM, 1979. Spatial Inventory and Modeling of Shifting Cultivation and Forest Land Cover of Northern Thailand, with Inputs from Maps, Airphotos, and LANDSAT, NASA/ Goddard Space Flight Center, Tech. Rep. Greenbelt, Maryland.
WACHARAKITTI, S., L.D. MILLER, AND C. TOM, 1975. Tropical Forest Land Use Evolution/Twenty year Landscape Model with Inputs from Existing Maps, Historical Airphotos and ERTS imagery. Colorado State Univ., Environmental Engineering Tech. Rep. 1, Fort Collins, Colorado.
TOM, C, AND L.D. MILLER, 1978. Spatial Inventory and Modeling of Land Use/Denver Metropolitant Area, with Inputs from Maps, Airphotos, and LANDSAT, NASA/Goddard Space Flight Center, Tech. Rep., Greenbelt, Maryland.