| GISdevelopment.net ---> AARS ---> ACRS 1990 ---> Digital Image Processing |
Digital Rectification for
Slar Imagery
Wen wogen, wang Xuquin, Liu Yuxian
Research Institute of Surveying and Mapping
Beijing , China
Wen wogen, wang Xuquin, Liu Yuxian
Research Institute of Surveying and Mapping
Beijing , China
Abstract
A SLAR imagery is a slant-range imagery with scanning dynamically. There are the deformation differing from air-photograph. This paper discusses how to pixel to pixel for SLAR imagery with a DTM. The experimental results are Mx = 12.8 meter and My= 11.0 meter using SLAR imagery revolution 0f 3-meter.
Introduction
Imaging radar transmits itself the pulses of microwave energy to shine the earth. It operates entirely independent of sunlight. So it has strongly penetrating power of cloud, rain and fog as well as imaging capability of all weather and day and night.
A side-looking airborne radar (SLAR) of synthetic aperture has a high resolution, sharp imagery and big covered area. The SLAR imagery, therefore, has wide application potentials . The experts, in early 1970s , had successfully experimented on mapping of the Amazon valley using SLAR imagery . Later on many countries had extended such an application. At that time, the mapping scales almost were 1:250,000 to 1:100,000. Digital rectification we do now is a primal part for the scale of 1:50,000 mapping revision with SLAR imagery.
Geometric Analysis of Slar Imagery
A SLAR imagery is created by which the distance (R) and its change rate (Dr) are determined measuring the delay time of pulses and Doppler shift. Owing to the result of radar ranging, there is an imagery point for the different ground points. It is called as radar layover. At the same time, the geometric deformation of SLAR imagery will be generated by a variety of errors of radar system, flying behavious of aircraft and environments. Most of the operating errors of the radar system will be compensated. The environmental influences are, however, still existence.
For cartography, first of all the ortho-position of SLAR imagery must be solved. Suppose the terrain surface is a flat one, due to distant projection, the imaging scale of the slant-range imagery is not uniform, the further off an antenna a target, the bigger a scale of imagery, and the nearer an antenna, the smaller a scale. This is called as the scale compression. The larger the depression angle of antenna, the more serious of compression (M ‘ = M/cos (phi). This is a non-linear in-fluence. So transforming the slant-range imagery to distant imagery have the error of the scale.
The terrain relief, however, is quite general case and the displacement of imagery is always come into existence. The displacement of imagery generated by terrain relief are taken place always in the side looking plane and parallel one another. Suppose a hill called as ABC shown as figure 1. There are the foreslop surface AB and the foreslop angle (alpha), the backslop surface BC and the backslop angle (bet) and an elevation h above the average sea level. If (alpha) >) theta, u)
Fig. 1-a
Fig. 1-b
(Fig. 1-a), the imagery of the slop surface AB and BC will generate the layover each other. If (beta) > (theta.d) (Fig.1-b), the radar beam does not illuminate the backslop surface. So the shadow BsDs is generated by the backslop surface BC and the flat ground CD. if (beta) > = (theta d) the backslop surface BC is fully illuminated with the radar beam and then non-shadow will be take place. Generally speaking, the displacement and shadow of the SLAR imagery is a function of the terrain relief except the radar line. So it is the best to perform fine geometric rectification with a DTM.
1. Coordinate Equations of Radar Imagery
The coordinate equations of radar imagery for applying to digital processing is derived as Figure 2. Assume Ng is equal to Dg, it is called as the delay distance in which non-imagery is happened. The Y is for the scanning direction and the X is for the direction of flight of perpendicular to the Y through the point N. The point P, Pg and the arc (PPg) have the same range arc (PPg} have the same range (R) . If h is given, it is possible to work precisely out the ortho-position P of point P:
Fig. 2
Y= [(Y2+h2-aHh)1/2 –Dg}/ My (2)
where Mx, My ------- scale denominator of the SLAR imagery It is easy to find both x and y or X and Y is independent each other in a side looking plane, and the imaging coordinates will be solved wit a DTM.
2. The Earth Curvature Influence
Because of the radar scanning of wide scope, it is neccessary to consider the earth curvature influence and correct it in each scanning line. The formulation as following:
| E2 = r2 | R2- (H-h)2 ------------------- (H+r) (r+h) | (4) |
where
r----- the earth radius;
H----the antenna heigh;
h----elevation of groundpoint;
R----the range between the antenna and target.
3. Atmospheric Refraction Influence
The path of the microwave transmission is bent caused by atmospheric refraction, which is the same thing with the other electromagnetic waves. The path radius (r) is calculated following Lauyila’s formulations:
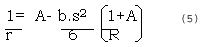
where R --- the earth radius, s—the range , A= a+b (H+h), a -3.7 X 10 and b= 1.4 X 10.
Here is only in consideration of the influvence for the different refractive indexes as following:
where dn----the difference between actual refractive indexes.
Least Square Fit
After the systematic errors are corrected, the discrepancies between calculated and measured the coordinates of imagery will still existe. The discrepancies are produced mainly by the errors of radar system, the optical correlator, computation and unknown erroneous resources and can be fitted with the least squares method as following :
mxn 1xn 1xm (7)
where
A--- matrix of the coefficience; X--- matrix of unknown;
B---matrix of discrepancies; m--- number of image point;
n---number of unknown.
If the scale of imagery are considered with both directions of X and Y, the formulations of a point are:
DY = B0 +B1X+B2Y+B3XY+B4X2 (9)
where the relationship between imagery point error Dy and Y in the scan direction is considered as the linearity.
The Experiment and Result of Digital Rectification
Digital rectification is a complicated technical processing of pixel to pixel.
- The kernel programmed of digital rectification is performed by FORTRAN code. This programmed will check automatically up the partition whether or not reasonable (is for threshold and hi for the value of DTM). Then the partition is performed automatically. The coordinates of four corners each partition must be worked rigorously out and the linear transformation will be done inside each one. One dimensional resembling of big array is produced with double buffers and the computer time is saved.
- The jointing, mosaicing and matching of the SLAR imagery will be performed by PIPS image processing system developed by RISM. The imagery rectified is output with the map size of the scale of 1:50,00
- A DTM data can be read in from existential DTM data base or pick up from topographic map. The interval of a DTM can be chosen as 100 meter.
- A man-machine dialogue for the evaluation system of accuracy.
A conclusion can be made as mentioned above. After digital rectification of 3-meter, the plane accuracy will meet the case of mapping of 1:50,000.
References
- F. Leberl Itc Technical Report, 1978
- A new Three-meter Synthtic-Aperture Radar For Earth Resources Studies, Goodyear Aerospace Co., March, 1985