A Remote Sensing model for wheat drought monitoring

A Remote Sensing model for wheat drought monitoring

Yang Xihua Tian Guoliang
Institute of Remote Sensing Application, Chinese
Academy of Sciences, Beiling 100101, P.R. Chian

Abstract
This paper presents a remote sensing approach for wheat drought monitoring and modeling, which based on the principles of soil water balance and energy balance. The initial soil water content ( Wo) was obtained from the relationship between the apparent thermal inertia and soil moisture which was established through the experiments conducted over nearly bare fields on the North China Plain. The evapotranspiration (Et) of the wheat field was estimated using the remotely sensed reflected solar radiation and surface temperature extracted from the NOAA-AVHRR digital image as well as the meteorological data such as incoming solar radiation, air temperature, wind speed and vapor pressure from ground meteorological station. Then the solid water content ( Wt) in a certain period of time ( 10 days ) can be calculated using the equation of soil water balance., At last, a drought index model was developed by concerning the available soil water content and the wheat water requirement. This model has been proved to be practicable in monitoring the wheat drought in parts of the North China Plain.

Introduction
Drought, a worldwide problem, is one is the most critical restrictive factors in plant survival and development. In China, especially in the North China Plain, drought is the most serious natural disaster and it accounts for half of the total agricultural loss. Therefore, the research the practicable methods for plant drought monitoring in order to take immediate measures and strategies of prevention is very important and meaningful.

However, its very difficult to monitor the crop drought due to its dynamic nature and regional variation. Although a lot of researches have been done in this field, there are still many difficulties in methodology left unsolved.

The traditional methods, such as meteorological methods and soil hydrological methods, can in some extend display the plant water status. But they have no exact agricultural meanings be caused they have no relation with crop water requirement. In the meantime, the traditional methods for determining drought are essentially point measurements. It’s difficult to acquire the numerous samples to present the characterize fields and impracticable to apply to a large area. Whereas, remote sensing techniques provide large area coverage and can obtain the surface information rapidly and multitemporally. The means of remote measurement could open a new way for drought monitoring and bring it into practicable service.

The most important factors related to drought are the soil moisture and evapotranspiration. Many researchers have contributed excellent articles on the acquiring of those parameters by remote sensing means. Sherwood B.Idso (1975) and John C. Price (1977 and 1980) have developed the thermal inertia approach for remote sensing of near – surface soil moisture. Although the model was based on simplifying assumptions, it’s useful in application on the bare or low-cover soils.

Presented at the 12th Asian Conference on Remote Sensing, at Eegional English Language Center, International House of the South Asian Ministers of Education Organisation ( SEAMEO ) , 30, Grange Grove Road, Singapore from October 30 to November 5, 1991. Toby N. Carlson, etc. ( 1980), G. Russell ( 1980) and R.D. Jackson ( 1981 and 1982) suggested that the plant temperature ( or leaf-air-temperature ) may be an indicator of soil moisture. They developed a range of methods to estimate evapotranspiration using plant canopy temperature and net radiation derived from energy balance and converted it into a crop water stress index 9 CWSI), which closely parallel to the extractable soil water content within the root zone. A comprehensive review of research on remote sensing of surface soil water content within the root zone. A comprehensive review of research on remote sensing of surface soil moisture has been presented by T. schmugge ( 1978), It’s instructive to our research. In this paper, we’ll apply the principles of energy balance and soil water balance to develop a remote sensing model for wheat drought monitoring. This model concerns the wheat water requirement and the available soil water content as a whole, and most of the parameters involved in this model can be derived from NOAA-AVHRR. It’s expected to be practicable to apply to the North China Plain.

Theory and Methods
The soil water balance is defined as:

DW=W_t – W₀ = P + I – R - F + C – ET----------------(1)
where DW is the variation of soil water content in )—1 m soil zone within the study period, W_t is the soil water content at the end of this period , Wo is the initial soil water content, P is the precipitation, I is the irrigation, F is the infiltration, C is the capillary – rising water and ET is the evapotranspiration. All those parameters are expressed in MM.

The P + I - R - F in the above equation can be regarded as the retentive water o the precipitation and the irrigation in certain soil zone, and can be replaced by RW ( that is RW = P+I-R-F). Then the equation (1) can be rewritten as:

W_t = W₀ + RW + C – ET -------------------------- ( 2)
Experiments show that the capillary – rising water is too little to be measurable when the ground water level is below 3 meters. So, it’s reasonable that C can be ignored since the groundwater level in most parts of the North China Plain is blow 3 meters ( some parts even reach 8.5 meters ). Then we have:

W_t = W₀ + RW – ET ------------------------------- ( 3)
This equation suggests that the variation of soil water content is mainly depended on the retention of precipitation and irrigation in the soil and the field evaportranspiration. the determinations of those parameters are discussed as follows:

1 Initial Soil Water Content (W_o)
The initial soil water content is regarded as the soil moisture in the beginning of the study period. In this research, we select the early spring as the concern. This time the winter wheat in the North China Plain is begin reawakening and the soil is nearly bare or with lower cover. We adopted the thermal inertia method to estimate the soil moisture. The soil thermal inertia (P) can be expressed as:

P=(lrC)^½ ------------------------------ (4)
where l is the thermal cond9uctivity ( JM^-1S^-1K^-1), r is the soil density ( K_gM^-3) and C is the specific heat ( JK_g^-1 K^-1) . The thermal inertia P(Jm^-2K^-1S^1/2 ) is the internal factor which affects the amplitude of the diurnal temperature. Their relation is:

D T(t) = V cos (wt -p/4 ) / (ÖwP )-------------------------------- (5)
where V is the amplitude of surface heat and is the frequency of earth rotation (7.27 x 10^-5S^-1). (5) was simplified by Price (1977) and described as apparent thermal inertia:

P = 2SVC₁ ( 1-A) / vw ( T s(13:30) – T S(02:30)) – 0.9B /v w -------------------------- (6)
where B is the temperature coefficient, T s13:30) and T s(02:30) are the surface temperatures at 13:30 and 02:30 respectively. Those factors can be derived from satellite imagery.

It’s easy to see that the thermal inertia is the function of soil surface temperature and the albedo (A). We use the total downward solar radiation (Q) to replace SVC land get:

P=2Q ( 1-A) / DT ----------------------- (7)
The Q and A can be acquired from CH1 and CH2 and from CH4 of NOAA-AVHRR respectively. Through the experiments conducted on the North China Plain during 1987 and 1989 ( Sui and Tian, 1990), we established the relationship of the soil moisture and the apparent thermal inertia. With this relationship and the equation (7), the soil moisture at the upper 10 cm was estimated and the mean relative error was about 14%.

2 Retentive Water ( RW)
Wo the infiltration theory in a practical situation, we must make some simplifying assumptions. in this study, we assume that the precipitation or irrigation infiltrate into the soil by the end of a certain period, and the way of infiltration is from the upper layer to the second layer and so forth. It continuous when the upper layer reaches the field moisture capacity (FMC) and where are still more water. If all the soil layers within one meter reach the FMC, the surplus water permeate out the one meter colume. The retentive of entered water can be expressed as:

RW( I,t) = FM C(i) – SW ( i,t – 1) --------------------- (8)
As to one meter soil colume with three layers:

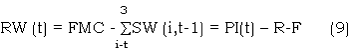
where RW(t) is the net percolation of the I layer in t day (days), SW (I,t-1) is the soil water storage in I layer in the day before t. The infiltration (F) is mainly determined by precipitation and the soil conditions ( Soil texture, soil moisture, groundwater level). According to the experiment conducted on the North China Plain, the infiltration occurs only when the precipitation is larger than 15 mm, and it can be estimated from:

F = aP ( P>15mm) ------------------------ (10)
Where a is the infiltration coefficient, and it can be looked up from the hydrological manual.

The runoff ® on North China Plain is relatively small and can occur only when the precipitation is larger than 80 mm. That means R=P-80.

With the above concerns, the retentive water of precipitation and irrigation can be obtained.

3 Evapotranspiration (ET)
The actual field evapotranspiration, which not only depends on the atmospheric conditions

But also has close relations with the soil and crop, is difficult to analyse because of the many contributing factors. Concerning the soil-plant – atmosphere as an integration, the methods of estimating evapotranspiration over large areas by using the NOAA-AVHRR in conjunction with meteorological data were developed ( Tian etal, 1989).

R_n = H + LE + G or LE = R_n – G - H ------------------------- (11)
Where Rnis the net incoming radiation flux, His the sensible heat flux from ground to atmosphere, and Gis the energy into the ground. All fluxes are in units of energy per unit time per unit area (W/M^-20) .

According to the preceding researches and our experiments, we define:

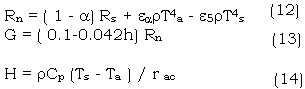
Where Ais the albedo, Rs is the solar radiation, ea and es are the emissivities of the air and ground surface respectively, r is Stefan – Boltzmon constant ( 5.67 x10-8) , h is crop height (m), r is air density ( Kgm-3), Cp is the specific heat of air (JKg-1C-1 and rac aerodynamic resistance (Sm-1). The albedo (A) was calculated from NOAA-AVHRR CH1 and CH2, and Ts are from CH4. The other parameters were got from meteorological data. Therefore, the remote sensing estimation of crop evapotranspiration can be realized.

4 Water Requirement of Winter wheat
The water requirement of winter wheat is in great difference in the different growing periods. Generally, it is higher before winter due to the higher soil evaporation. In winter, it reaches the smallest because the temperature is low and the wheat nearly stop growing. After reawakening ( the end of march), the temperature increasing and the leaf area enlarging, the water, it decreases with the decreasing leaf areas and chlorophyll content. With the assumptions that the wheat is grown under the normal weather conditions and middle fertility, the water requirement of winter wheat in a certain period can be calculated by.

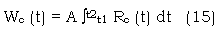
Where A is the coefficient of water requirement related to crop breed and yield , t is the growing period ( in days), is the daily water consumption which can be determined by

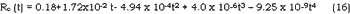
With (15) and (16) we can figure out the water requirements for any time in the growing period.

5 Drought Index
In order to display the nature of drought , we defined a crop drought index (D) which combines the soil available water content and the crop water requirement:

D = (W_t - W_w ) / W_c ------------------------ ( 17)
Where W_w is the withering water content (mm) W_c is the crop water requirement (mm).

According to the damage degrees to winter wheat, we divided the drought index into five grades (Table 1) .

Table 1 The Grades of Wheat Drought Index

Water Status	Moist	Normal	Light Dry	Dry	Heavy Dry
Drought Index	> 1.2	0.8 – 1.2	0.5-0.8	0.3-0.5	<0.3

Data Analysis and Treatment

Data Acquisition
The NOAA – AVHRR CCTs of March 7, and May 4, 1990 were acquired from the National Satellite Meteorological database in order to analyse the meteorological stations and our field measurements.
Database
It’s necessary to build a meteorological database in order to analyse the meteorological condition systematically, get data quickly and prepare for the rapid drought predication. Surported by DBASE, the meteorological database was built under the items of air temperature, precipitation, solar radiation, wind speed and humidity for every 10 days from March to June during 1979 and 1990. It has the functions of rapid inquiring, indexing, replacing and calculating.
Image Processing
Following the methods discussed in 2.1 and 2.3, we obtained the initial soil water content (W0), evapotranspiration (ET) and soil water content (Wtt) from the NOAA-AVHRR CCTs and database with our image processing system. Finally, the drought index of winter wheat was calculated and the map was drawn according to the definition given in 2.5.

Results and Discussions

Fig 1 Drought Index Map of Beijing, Tianjin and Parts of Hubei
Figure 1 is the map of wheat drought index of May 4, 1990 Beijing, Tianjin and parts of Hubei province. We can see from this map that most parts of the northeast are normal (0.8<D<1.2), the southwest show there is dry, and only a few belongs to the moist condition. Those are in accord with our field measurements.

However, there are still some questions left to be discussed:

The irrigation in the water balance must be concerned. A practicable model related to the hydrological engineering and irrigation practice should be built.
The division of the drought index grades should concern the regional variation of crop and soil.
The capillary – rising water in the region with low ground water level should take into account.
The geographic information system is necessary of drought monitoring and predication of large area.

Conclusions
The drought monitoring model, which bases on the principles of energy balance and water balance and concerns the soil available water content in conjunction with the crop water requirement, appears to be practicable for assessing wheat drought. The methods for estimating the initial soil moisture and evapotranspiration are also sound and acceptable. However, we are still at the beginning of the development of a rapid monitoring and predicting system which supported by GIS and can be put into practical service for large area.

Acknowledgemnets
The authors would like to thank Mr. Zheng Ke and Ren Fuhu for image processing, and Mr. Yang Xiaohuan and Lu Youghong for field measurements.

Refereces
G. Russel, Evaporation, Surface Resistance and Soil Water Status, Agri. Meteor., 21:213-226, 1980

John. C. Price, Thermal Inertia Mapping: A New View of the Earth, J. Geophys. Res., 82 (18): 2582 – 2590, 1977

John. C. Price, The Potential of Remote Sensing Thermal Infrared Data to

Infer Surface Soil Moisture and Evaporation, Water Resour. Res.. (4):787 – 795, 1980

Ray. D Jackson, S.B. Idso, R.J. Reginato and P.J. Pinter, Canopy

Temperature as a Crop Water Stress Indicator, 17 (4): 1133 – 1138, 1981

Sherwood. B. Idso, etc., Compensating for Environmental Variability in the Thermal Inertia Approach to Remote Sensing of Soil Moisture. J. Appl. Meteor ., 15:811 – 817, 1976

Toby N. Carlson, J.K. Dodd, S.G. Benjamin and J.N. Cooper, Satellite Estimation of the Surface Energy Balance, Moisture Availability and Thermal Inertia, J. Appl. Meteor., 20:67 – 87, 1980

T. Schmugge, Remote Sensing of Soil Moisture, J. Appl. Meteor., 17:1549 – 1557, 1978 Sui. H.Z. and Tian. G.L, Monitoring Soil Region in the Yellow River Vally, Science Press, 1990

Tian. G.L. etc., Estimating of Evapotranspitation and Soil Moisture Using NOAA – AVHRR Image and Ground Based Meteorological Data, Proceedings of 10th Asaan Conference on Remote Sensing, 1989