Abstract
A growing season of crop from planting to harvest is a complicated process. There are many factors that influence final yield which is the comprehensive response of various factors, such as environmental conditions, biological factors and agricultural management and technique etc. Thus only Remote Sensing information or meteorological data do not reflect the conditions of crop growth actually. In this paper, an example in Shunyi County, Beijing, China, is given, a winter wheat yield comprehensive model is proposed. The model is combined perpendicular Vegetation index (PVI) with meteorological data. A grey-system model GM (0,2) and a successive corrected method were used to establish a Remote Sensing - meteorological dynamic model for estimating winter wheat yield. By using multitemporal NOAA-AVHRR imageries and air temperature, the average accuracy of yield estimation is improved 7% in the comprehensive model than in the PVI model only.

Introduction
Bumper or shortfall harvest of grain production has large influence on economic development of China that owns 1.1 billion population. It is strategically important for timely and accurate crop production estimation.

Agricultural total production is product of planting area and yield, therefore production estimation may be divided into yield estimation and area prediction. Because planting are has not large yearly fluctuations, it is directly estimated by Remote Sensing information. However, it is difficulty to estimate yield for it depends on several factors which vary seasonally and annually and interactions among them are very complex.

Yield models have been studies for a long time. There are many methods, for example, agricultural forecasting, statistical prediction, agrometeorological statistical forecasting and Remote Sensing information forecasting et al.. The models gained by using above methods were established in their own ways, however, yield is a result of comprehensive response of various factors and methods proposed above do not reflect the conditions throughout crop growing season actually. Even if the models of vegetation indices which are composed of visible and near-infrared reflectance have more merits than other models, they are only reflected green crop growth around heading, it can not reflect the conditions of late growth of crop. Hence, if the yield model is established with a piece of information, the accuracy of yield estimation is neither high nor stable.

In this paper, a new comprehensive model is put forward based on the merits and demerits existed in various yield models proposed above. In the model, a vegetation index which reflected crop growth and average air temperature of the milk-filling period of winter wheat are considered as main factors affected wheat yield. A grey-system model GM (0,2) and a successive corrected method were used to establish a Remote Sensing - meteorological dynamic model for estimation yield.

The Grey-System Model
System which partly information has been known is called grey-system. It has a new viewpoint and thinks that any random processes are grey amount changes within range and time. The random process is regarded as grey process. It looks for a numeral law by putting primary data in order and then establish a predicted differential equation. Merits of the grey-system model are that it need sample neither size nor a typical distributive law.

The GM (0, h) model ⁽⁸⁾is a linear model which has h variables included independent variables and deponent variables. Steps that the model is established are :

First, primary data, which may be disorderly and unsystematic, are accumulated generating operation in order to establish the grey-system model. Then we get generating operating sequence Xi(1), and the two sequences are satisfied with relation listed below:


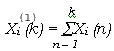
Where : X_i⁽⁰⁾ (n) -- value of the i primary data sequence for nth time
X_i ⁽¹⁾ (k)- value of i the generating operation sequence for kth time

Second, coefficients of the model are calculated. General form of the GM(0,h) model is :


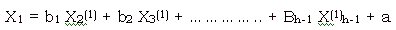
Matrix of coefficients is :


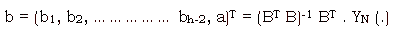
where


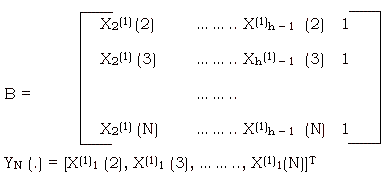
Where :N is number of samples

Third, data obtained from above the model must be return to data which are not accumulated generating operation. It s ordered that X(r) is the generating operation sequence of r times and a(i) is inverse accumulated generating operation of i times, the general form of the return primary data model is :


where : a(0) is no inverse accumulated generating operation

The Successive Multiplied Model
Yield of crop is the result of continuous accumulation throughout the crop growing season. There is not a factor which can reflect the all conditions of crop growth, and it is also difficulty to unite all factors into one predicted model. How can we establish a dynamic yield model that may be reflected all period of crop growth? The successive multiplied model proposed recently has been used to solve the problem put forward above. A basic equation of the successive multiplied model :


where : Y_t is yield of the t development stage of crop
Y_t-1 is predicted yield of the t - 1 development stage of crop.
X_i is a predictor of the t developmental stage of crop
By using the PVI and the GM(0,2) model, we get the predicted yield model before heading.

Y₁ = V_i1 (X_1i)

When the primary yield sequence Y₀ is divided by the first predicted yield sequence Y1, a new sequence Y1' is gained.

Y0i/Y1i = Y1i

Then by using metrological factors of late crop growing periods and the GM (0,2) model, we get the corrected model of yield.

Y₂ = V₂ (X₂)

Final predicted yield is :

Y = Y₁ * Y₂

A model of dynamically estimating yield is obtained form above methods. If we require more corrected values or different temporal, we may establish third or forth corrected models. Predictors are from on to h - 1 in the GM(O,h) model. And the final predicted yield is product of the first predicted value and various corrected values.

Vegetation Indices
Linear transformations of reflectance values of spectral bands to vegetation indices express the spectral behaviours of crops and vegetation in a simplified manner. According to study of Kauth-Thomas and Jackson , a Perpendicular vegetation Index which is perpendicular distance to the soil line is superior to other vegetation indices as a ratio vegetation index and a normalized difference vegetation index etc. It is sensible to vegetation conditions and not much affected by background and atmospheric variations. Therefore, it has been used in this paper. By using 1986.3.1, 1989.3.7 and 19900.3.15 three days NOAA-AVHRR spectral data of bare soil, we got the soil line of Shunyi as following :

CH₂ = - 1.6354 + 1.2730CH1 R = 0.9602 N = 272

Where : R is coefficient of correlation, N is number of pixels, CH, CH2 are reflectance clues of the channel 1 and 2 for AVHRR, respectively.

By transforming the soil line, a calculated formula of PVI is :

PVI = 0.6177CH₂ - 0.7864CH₁ + 1.0103

Result and Discuss
Due to location in Beijing suburbs, the production of Shunyi is managed in scale and its mechanism, is high. So its production forced even. It is convenient to establish an average yield model by using average PVI values for all pixels in the Country. The PVI of per year listed in table 1 was correceed by accumulated temperature in a same development period.

Table 1 PVI of the heading period in Shunyi

Year	86	87	88	89	90
PVI	4.3130	5.9908	5.7965	5.0234	6.23665

Main factors that influence late growing period of winter wheat are temperature and precipitation. In Shunyi county, fields of winter wheat are sprayed irri- gation, it is only temperature as main factors affected winter yield. By screening, we choose average air temperature of last decade of May as meteorological factors. Table 2 represents the average yield and the average air temperature, which are obtained form the statistical service and the meteorological station of Shunyi respectively.

Table 2 average yield and average air temperature of last decade of May

Year	86	87	88	89	90
Yield(jin/mu)	595.1	637.3	674.2	733/9	754
Temperature (0°c)	23.4	20.7	19.1	23.3	19.7

The first forecasting model which is relation between yield and PVI is established by the GM(0,2) model introduced above.

Y₁ (k) = 120.3212PVI(k) - 108.9294

By using the return primary data model, predicted yield and its relative errors are listed in table 3.

Table 3 predicted yield and relative errors by using PVI as predictor

Year	86	87	88	89	90
Y1(k)	595.1	1213.3	1956.1	2601.7	3402.0
Y1	595.1	618.2	743.8	644.6	800.3
Relative error	0	-3.00	10.33	-12.17	6.14

In the same way, by using the GM(0,2) model, a corrected model was established between new sequence which is obtained from above methods and the average air temperature of last decade of May :

Y₂(k) = 0.048196T - 0.099143

Where : T is the average air temperature of last decade of May.

Table 4 represents the predicted yield which is product of first predicted yield and temperature corrected value that is calculated by the corrected model and accumulated generating operation and relative errors.

Table 4 : Predicted final yield and relative errors

Year	86	87	88	89	90
Y1(k)	1.0000	2.0263	2.9468	4.0698	5.0193
Y2	1.0000	1.0263	0.9205	1.1230	0.9495
Y1	595.1	618.2	743.8	644.6	800.3
Y	595.1	634.4	684.7	723.9	759.8
Relative error		-0.45	1.56	-2.37	0.77

By comparing table 3 with table 4, we know that crop yield is not increased with PVI. If the model is established by PVI as predictor only, errors are large and the result is not good. But if the predicted yield is corrected by metrological elements of late crop growing periods, the accuracy has obviously improved. It is not only that average accuracy of yield estimation is improved 7% but also yearly errors are more steady in the comprehensive model than in the PVI model only. It is also show that meteorological conditions which influence late crop growth are not ignore. So when a yield model is established, the meteorological factors must be considered.

Due to particular situation of Shunyi, we only average temperature of last decade of May as a meteorological factors. In fact there are many meteorological elements, for instance, solar radiation, temperature and precipitation etc, which influence winter wheat from heading to mature stages. When the predicted model is extrapolated to the other area, it is must be increased other factors.

Reference

• Liu Guoxiang 1987, Collected works of the technology and methodology researches on remotely sensed winter wheat estimation in the Beijing - Tianjin-Hebei District, Beijing science and Technique Publisher (in Chinese).
• Xiao Qinguang et. al, 1986, Productivity estimate using meteorological satellite Remote Sensing of Environment, Vol. 1, No. 4 (China)
• Barbect T.L. and Thompson D.R., 1983, Large-area relation of Landsat MSS and NOAA-6 AVHRR Spectral data to wheat yields. Remote Sensing of Environment. Vol.3, No. 4 (China).
• Xiang Yueqin, Tain Guoliang, 1988, Estimating rice yield form remotely sensed data - I Relating Yield to total intercepted radiation. Remote Sensing of Environment. Vol. 3, No. 4(China).
• Tian Guoliang, Xiang Yueqin, 1989, Estimation of rice yield from remotely sensed data - II Based on Spectral reflectance and Landsat images . Remote Sensing of Environment, Vol. 4, No. 1(China)
• Li Yuzhu et al, 1990, The studies and experiments on synthetic prediction of winter wheat production in China with NOAA polar orbiting satellite data. Proceeding of the 11th Asian Conference on Remote Sensing, Vol. 1, A - 2 - 1
• Xu Xiru et al, 1990, The Method and practice of macro Remote Sensing monitoring of winter wheat. Proceedings of the 11th Asian Conference on Remote Sensing. Vol. 1, A - 1 - 2
• Deng Julong, 1986, The Controllable Grey-System, Center Chinese Technology University Publisher.
• Kauth R.J. and Thomas G.S., 1976, The ta sseled cap - a graphic description of the temporal development of agricultural crops as seen by Landsat, proceedings of the Symposium on Machine Processing of Remote Sensing Data. Purdue university, PP.4B/41-51
• Jackson R.D., 1983, Spectral Indices in n - space, Remote Sensing of Environment 13, PP.409-421