Use of Landsat thematic mapper data for extracting topographic information of a rugged forested region in Indonesia

Use of Landsat thematic mapper data for extracting topographic information of a rugged forested region in Indonesia

Waqar Ahmad
Department of Geographical Sciences and Planning
The University of Queensland, Brisbane, Australia

Abstract
The effects of shadows has been and major source of concern in the remotely sensed data classification of a rugged forested region. The severity of the problem magnifies especially in the developing countries where either the topographic maps are non-existent or the quality of the existing maps is extremely poor. In this paper an attempt have been made to evaluate the applicability of Landsat Thematic Mapper data fro extracting the topographic information. A radiance model used to reflectance is applied to a forested region of Indonesia to generate a topographic image.

Introduction
During the last two decades considerable research have been carried out towards the applicability of remotely sensed data for land cover mapping in various part of the world (Ahmad, 1986). Unfortunately, mapping land cover types had limited success in high relief areas. This is mainly because of the varying facet slope and orientation which causes marked variation in the spectral signatures appearing on the Landsat images. As a result cover types may have similar spectral reflectance but quite different radiances to the shading effect of topography. This makes the classification process extremely difficult.

Various researchers have used number of techniques to subdue the topographic effects. This includes the use of band ratioing ( Justice, 1978; and Holben and Justice, 1981, Ahmad, 1986). Some researchers used multidimensional analysis using digital topographic data as added dimensions and physical models which estimate the reflection of solar radiation from slopes (Smith et al. 1980) ; Kimes and Kirchner, 1981; Teillet and Good enough, 1982; Kalsh, 1987 and Lepricurand and Durand, 1988).

In this paper topographic effects have been analyzed using a radiance model suggested by (Ahmad et al. 1991). Underlying idea behind this approach is not only to define classes on the basis of both spectral similarity and illumination,, that is, sunlit versus shadowed but also the extraction of topographic information from the classification of Landsat Thematic Mapper data.

The image processing tasks of this project were carried out using micro BRIAN software at CSIRO, Division of Water Resources, Canberra, Australia. The micro BRIAN system is a microcomputer based image processing system. For further details on the system see Microprocessor Applications Ltd. ( 1987).

Study Area
The research was undertaken in the Mouton region of Indonesia. The northwest and southeast coordinates of the study area are 0° 45’ 05” N, 121°10’ 15” W and 0°40’ 10” S, 121°15 30” E. The major reason for its selection was the rugged nature of the study area and availability of aerial photographs of the study area. Moreover, non availability of the topographic maps of the area lead to its selection.

TM Data Classification using Landform information
The following section provides details of the various steps followed and the salient features of the mathematical model used.

Model Description
Consider a Landsat scene encompassed by N Pixels (i = 1 to N), n_b banon (j = 1 to n_b) and nc values of land cover (k = 1 to n_c). In terms of lans cover, the total number of pixels in the scene (N) can be described as

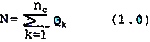
Were Q_k denotes the number of pixels in the scene which fall under land cover category k. Using this labelling convention, the satellite recorded radiance in pixel I, channel (or band j and cover type k (Y) has the following form:

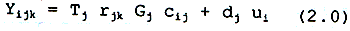
Where T_j is atmospheric transmission in band J, r_jk is reflectance in band for cover type k, G_j is irradiance in band j on a horizontal surface, C_j, the topographic modulation factor, dj is atmospheric path radiance, and u_j potentially an atmospheric inhomogeneity term (independent of wavelength).

The topographic modulation factor, C_ij, is 1.0 for a flat surface an less than or grater than one for slopes away from and towarcs the so respectively. For Lambertian surfaces (uniformly diffuse reflectea radiance and low or no diffuse incident radiation, C, takes the following form:

C_ij = maximum [cos (Z')/cos (Z), 0] (3.0)

Where Z is the zenith angle of the sun, Z’ is the angle between the sun vector and the normal to the slope. More generally, C_ij can be defined as modification of G_j such that:

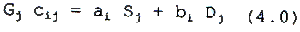
Where a_i and b_i depend on the local slope and aspect and S_j and D_j are the band specific direct and fiffuse irradiance terms such that G_j = S_i + D_j . That is

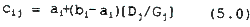
If we assume that [D_j/G_i is small or constant for the bands being used, the dependence of C_ij on j disappears and the model may be reduced to:

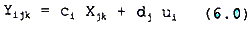
Where, X_jk is the composite term [T_j G_j r_jk].

When the atmospheric inhomogeneity term is negligible, then d_j u_j could be replaced by d_j. If the land cover is uniform, the model reduces further to:

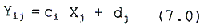
This form is identical to the one used by Switzer et al. (1981) to estimate d_j by the covariance matrix method (See Appendix).

When the land cover is not uniform, the effect of slope (C_i) can be eliminated and an expression for r_jk can be obtained which gives land cover unaffected by shading. For the purposes of the image classification presented here, a fact exploited by Wang et al. (1984) was used. This involved obtaining a ratio R_jlk which is related to the radiance recorded from the same pixel but at different wavelength bands.

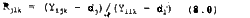
In the absence of noise in the Y_ijk this ratio approximates

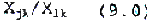
The above expression, if the d_j were known, is independent of c_i and only a function of spectral cover type. In practice, the presence of noise and model inadequacy makes Equation 9.0 a useful approximation.

The method used therefore, was to estimate the d_j terms using Switzer et al. 1981 and Appendix 1.0 method and to form ratio images or rather the logarithm of the ratio images obtained form Equation 9.0. The log ratio images were then classified using the microBRIAN image processing system, resulting in a set of spectral classes of generally uniform land cover type.

The next step was to extract the topographic (or shaded land form) component from the original raw data. This was accomplished by transferring the classes based on the log ratio image back to the logratithm of the data by assuming the following model:

From Equation 6.0, the logarithm of the radiance in pixel I, band j and land cover k is:

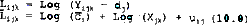
It is possible to average L_ijk for all pixels contained in a class. This procexure results in the estimation of a mean pixel radiance L_jk for band j and land cover k:

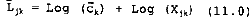
Where C_k is a mean topographic modulation factor for class k. In this way an image is produced which is identical to the mean image of the classification except that the L_jk replace the means of the log ratio. The residual image between this new mean image and the L_ikj image therefore has the following form:

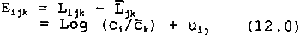
Here u_ij represents random noise, and L_jk and c_k are mean values taken over the k’ th ratio class. E_ijk has the form of a residual image (jupp and Mayo, 1982), between the log data and a computer based classification of it, which is free of the illumination variation.

The residual image E_ijk described in Equation 12.0 has only one linear factor (landform), which is independent of channel j. The first principal component (PC1) of E_ijk described as P_ik retrieves the relief and shading or brightness information.

If we assume that a complete range of aspects occurs uniformly in land

Cover classes, C_k will be approximately equal to a common value c. However even when C_k varies, it is worth noting that the variance of P_ik is a function of relief and that within high relief classes the relatively sunlite shaded areas can be threshold using p_ik

As a next step a composite image was formed by adding data from first principal component P_ik to the logarithm of the band ratios 1/2, and 4/3. Using p_ik a density sliced image was then created representing sum level by replacing the P_ik values. The composite image was then reclassification using the minimum distance algorithm. This process not only enabled produce a land cover classification taking care of the illuminate differences but also produce an image containing topographic information.

Conclusions
By using computer based classification of log ratio images in areas significant illumination variation, and the model based estimate of related and illumination as presented here, it is possible to reach very accum general land cover map and therefore, provide a base for large a for which topographic maps are non-existent, a quick first level information of the terrain of the area can be obtained by this method.

Appendix
In this study, an atmospheric path correction was calculated by used the covariance matrix method (Switzer, 1982). According to this technique radiance measured by the sensors over terrain with undulating form has components. Radiance contributed by the surface in the filed of view of sensor and radiance which does not originate from the surface within field of view. The former is information and the latter is termed noise atmospheric path radiance and noise. In model form, the measured radiance for pixel I ( as I runs over all pixels in the image ) and in band j can expressed as:

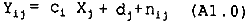
where C_i X_j is Information due to solar radiation reflected from the target d_jis atmospheric path radiance and n_ij represents unexplained noise.

The term c_i is a multiplier which describes the effect of pixel topographic orientation with respect to the solar beam during imaging for a Lambertian surface, and little or no diffuse irradiance, c_i equals cos 1 where L is the angle between the solar beam and the normal to the surface of pixel i. The term X_i is proportional to the average surface reflectance it spectral band j which is assumed to be uniform over the image. The proportionality factor is a product of a quantity which is not pixel specific over suitably small areas of interest. Therefore, according to Switzer.

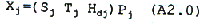
where
S_j = System gain factor in spectral band j
T_j = Atmospheric transmission from ground to satellite in band j
H_dj = Direct solar irradiance in band j
P_j = The constant reflectance in band j, assumed to be Lambertian.

The additive term d_j is the unknown atmospheric path radiance for spectral band j and consists of radiation scattered into the field of view of the sensor which never reached the surface.

The above parameters were estimated by using the covariance matrix method (CMM) technique ( Switzer, 1982). This method uses least squares to find a set of path-radiance values which minimize the sum of squares of the raw digital number minus estimates o the information plus path radiance terms. According to Switzer, if we average over i pixels then the Equation becomes:

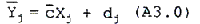
By subtracting Equation A3.0 from Equation A1.0 a matrix A can be obtained which has rank 1. That is,

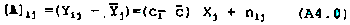
By taking the product of the transposition of the A matrix in this Equation with A, the image covariance matrix (ATA) can be obtained. This may be decomposed into eigenvalues and eigenvectors as:

where
l₁, l₂, l₃, ---------8n are eigenvalues
V₁, V₂, V₃ --------- Vn are eigenvectors

The application of Factor Analysis (Joreskog et al. 1976 ) to this case follows by noting that the expected covariance matrix, based on the model, has the form

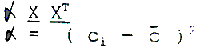
which can be equated to the first eioenvedcor anim coeigidoivoioiifkl dljfsfjklj dsljsdfj swith allowance for noise , as

Switzer computes a such that dz = 0 but often it is observed that dj> yjmin where c is yet to be determined. Effective dj values which do not give such results can be calculated by requiring that

References
Ahmad, W., 1986, Land use/cover mapping using remotely sensed data with special emphasis on application to forestry. A review of literatory 1973-1984. CSIRO Division of water and Land resources, Division Report 86/1.

Ahmad, W., Jupp, D.L.B and Nunez, M. ( 1991). Land cover mapping in a run terrain area using Landsat Mss data. International Journal of Remen Sensing. Forthcoming.

Jupp, D.L.B., and Mayo, K.K., 1982, The use of residual images in Landsat image analysis. Photogrammetric Engineering and Remote Sensing 48, 604.

Jupp, D.L.B., Heggen S.J., Mayo, K.K., Kendall, S.W., Bolton, J.R. and Harrison, B.A., 1985, The BRIAN Handbook. Natural resources series 3, Division of Water and Land Resources, Institute of Biological Resources, Commonwealth Scientific and Industrial Research Organization Australia.

Justice, C.O., 1978, An examination of the relationship between selects ground properties ad Landsat MSS data in an area of complex terrain southern Italy, Proceedings American Society of Photogram Albuquerque, New Mexico, pp. 303 – 28.

Kimes, D. and Kirchner, J., 1981, Modeling the effects of various radiance transfers in mountainous terrain on sensor response. I.E.O. Transactions on Geoscience and Remote Sensing, 19, 100-108.

Leprieur, C.E and Durand, J.M., 1988, Influence of topography on forest reflectance using Landsat thematic mapper and digital terrain Dan photogram metric engineering and Remote Sensing, 54, 491-96.

Microprocessor Applications pty. Ltd., 1986, microBRIAN software for image processing. Blackburn, victoria, Australia.

Smith, J.A., Ranson, K.J. and Kirchnern J.A., 1980, Simulation analysis bidirectional reflectance properties and their effects on -------- radiance. Implications for the MRS. Report to NASA, ORI, Silver Spring Marlyland, 125 pp.

Switzer, P., Kowalik, W.S., and Lyon, R.J.P., 1981, Estimation of atmosphen path – radiance by the covariance matrix method. Photogramme Engineering and Remaote Sensing , 47, 1469 – 76.

Teillet, P.M., Guindon, B and Goodenough, D.G., 1982, On the slope aspect correction of multispectral scanner data. Canadian Journal of Remote Sensing, 8, 84 – 106.

Walsh, S.J., 1987, Variability of Landsat MSS spectral responses of forest in relation to stand and site characteristics. International Journal Remote Sensing, 8, 1289-99.

Wang, S., Haralick, R.M. and Campbell, J., 1984, Relative elevation determination from Landsat imagery. Photogrammetric Engineering as Remote Sensing, 39 193-215.