| GISdevelopment.net ---> AARS ---> ACRS 1991 ---> Forestry |
The microwave emission of
layer with random bottom boundary
Chang Man
Institute No. 207, Ministry of Aero-Space Industry. P.O.Box 142-207, Beijing, 100854, China
Institute No. 207, Ministry of Aero-Space Industry. P.O.Box 142-207, Beijing, 100854, China
Introduction
This paper studies process of microwave emission of a homogeneous layer with smooth top plane and random bottom surface. We use an approximation and transmission of electromagnetic wave in the layer. For the sake of electromagnetic wave in the layer. For the sake of general purpose, we are using the model to be a layer with random bottom surface of two-direbitrary. The polarization states of incident wave can be horizontal or vertical. Due to the model is a layer with rough bottom surface, so, can produce cross polarization reflective components. In this paper, we have given out some calculating results of microwave emissivity or brightness temperatures. The polarization state can be either vertical or horizontal.
The Model and Coordinate Systems
Model:
The layer body is a homogeneous medium layer.
The top surface is plane.
The bottom surface is random rough surface with normal distribution.
Zoned Format.,
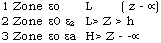
Where the relative dielectric constant e2 = 1.6 e3 = 5.0 The mean thickness of layer L O.06m. The heat source temperature to is 273°K.
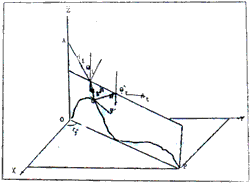
The coordinate systems.
The geographic system is 0-
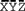 , the local Systems is o-
, the local Systems is o-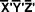 , to see Fig.1. please. Their
transformation relation is
, to see Fig.1. please. Their
transformation relation is 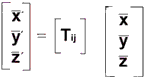
( Institute No. 207, Ministry of Aero-Space Industry, P.O. Box 142-207, Beijing, 100854, China)
The element of transformation matrix Tij are
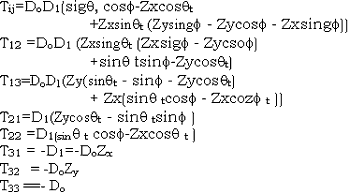
The renormalize coefficients
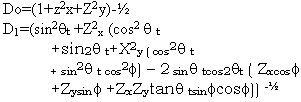
The direction of z is agree with normal direction of tangent plane of bottom surface, i.e.
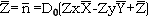
The incident wave vector
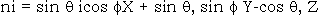
Where q, is incident angle in the geographic system.
In the local system, the unit vector of horizontal and vertical polarization can be written
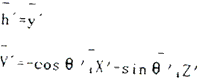
In the geographic system, the unit vector of transmission wave for izontal and vertical polarization can be written as
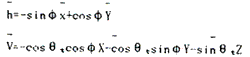
The Main Results
The brightness temperature of layer is consisted of two parts.
- Emission of top surface:
- Emission of layer with bottom boundary of random surface.
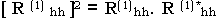
The reflective coefficient of horizontal pola rization
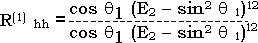
The reflectivity of layer with random bottom surface. The cross polarization reflectivity
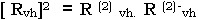
The horizontal polarization reflectivity
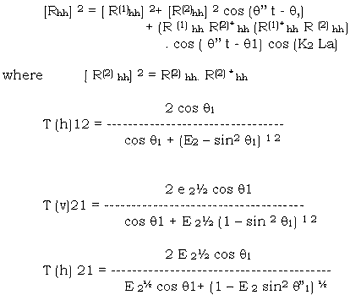
The brightness temperature of corresponding polarization states can be written
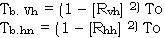
The vertical polarization incident wave. The reflectivity of top plane
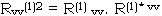
The reflectivity of layer with random bottom surface: The cross polarization reflectivity
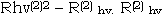
So, the vertical polarization reflectivity
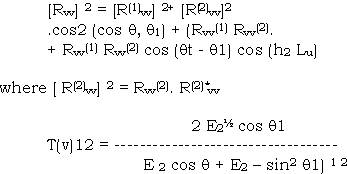
The brightness of temperature of different polarization states
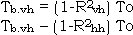
The distribution of slopes Zx and Zy is normal state
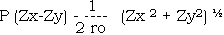
So, the results must integrate to Zx and Zy form to x.
The Calculating Results and Discussing.
- Because the slope Zx’ is projection along the Y-direction is Zesin q, so. Even if the slope of bottom surface Zy = 0. The effective Otherwise, if Zy = 0, f = 0, then R(2)vh = R(2)hv = 0. i.e. the reflection coefficients of cross polarization are zero. The Tb.hh and Tb.vv are shown as Fig. 2. and Fig.
- In any case of horizontal or vertical polarization incident wave. The brightness temperature of cross polarization wave Tb.vh2 and Tb.hv2 have same variance law with incident angle. To see Fig. 4 please.
- For horizontal and vertical polarization wave. The brigtness temperature Tb has same period on the range of 00 to 3600. Only if f = 900 and 2700, the brightness temperature Tb is maximum, and f = 180, the Tb is minimum, to see Fig. 5 please.
- The results of this paper is agree with A.K. Fung’s results.