Orientation of NOAA AVHRR Imagery with Few GCPs

Orientation of NOAA AVHRR Imagery with Few GCPs

Toshiaki Hashimoto, Shunji Murai
Institute of Industrial Science, University of Tokyo.
7-22, Roopong, Minato-ku, Tokyo 106, Japan
Tel : +81-3-402 – 6231, ext. 2560
Telex: 02427317 Kosmur J
Fax: + 81-3-479-2762

Introduction
In general, the geometric correction of NOAA AVHRR imagery is systematically carried out by using the satellite ephemeris data or the orbtal element data which are transmitted every day from NOAA. This method is called the system correction. There remain some distortions in the image by this method, as the ephemeris data have some errors and the variation of satellite attitude is not compensated. For the more accurate correction, these distortions have to be eliminated using ground control points ( GCPs). The authors have developed the system which enables to correct the orbital elements and the satellite attitude utilizing colinearity condition in photogrammetry. In the system, the position and attitude of a satellite are treated as exterior orientation parameters and they are determined with GCPs. Two colinearity equations can be made from one CGP, so the number of GCPs. Two colinearity equations can be made from one GCP, so the number GCPs has to be more than the half number of unknown parameters.

There are very few GCPs in the open ocean or on the cloudy image. Even in such a case, the geometric correction has to be carried out as precisely as possible for some applications, for example, monitoring the fluctuations of a certain phenomena from sequential images, mosaicing images, etc. The method of a precise geometric correction with few GCPs should be developed. For this purpose , it has been examined which orientation parameters should be corrected in case of acquiring only few GCPs.

Method of Geometric Correction
The satellite position and attitude are determined from co linearity condition used in photogrammetry, where they are treated as exterior orientation parameters. All parameters are functions of a line number as they very with time. The orientation is carried out on the geocentric coordinates system where the earth is expressed a reference ellipsoid. The image coordinates system is selected so that x-axis is along track and z-axis along the normal of satellite orbit. Under such a condition, the colinearity condition is expressed as follows. (Fig.1)

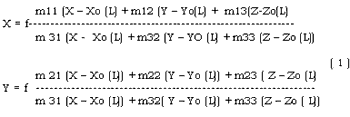
Where, F : assumed focal length
( X, y ) : image coordinates
( x, y, z, ) : Ground coordinates of object
( Xo, Yo, Zo ) : ground coordinates of satellite
( mij ): components of rotation matrix.

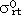
The satellite position (Xo, Zo ) on the geocentric co-ordinations expressed using the distance between geocentric and satellite ® inclination (i) , the latitude of ascending node ( W ) at any time (t) can be expressed using the epoch time (to) and the following 7 kinds of orbital elements { semi major axis (A), inclination (i), eccentricity (e), right ascension of the ascending node ( W ) , argument of perigee (w), mean anomaly (M) which are announced by NOAA. Consequently, the parameters to be determined are orbit elements ( A, I, e, W, w, m ) and satellite attitude ( w,f,k) . Each of then are expressed by a polynomials of line number.

Orientation Parameters to be Unknown
Two co linearity equations can be made from one GCP. The number of unknowns to be solved is limited in case of few GCPs. The order of priority which parameter should be an unknown is decided by the following conditions. (a) When some parameters have a big correlation, a representative among them is selected as the unknown and the others are fixed.

(b) The parameters which hardly vary with time are fixed.

Firstly, the residual patterns on the image were calculated when forced error was added to equation (1). The correlation coefficients between parameters were derived from these residual patterns ( Table 1 ) The result proved that there were high correlations between M_o, W_o and M₁ and W₁’ ) and , respectively. The residual caused by e_o was excellent along the track far from the perigee or the apogee and highly correlated with those by M_o or M₁. Secondly, it was examined how the variations of the ephemeris data had the influences of the residuals on the image. The actual ephemeris the residuals by their variations ere calculated. ( Table 2) From this result, the degree of the influences of the direction of along-track (Vx) and cross – track (Vy) is:

Vx : W_o, M_o > W₁, M₁ > e_o
Vy : W_o > i_o > M_o > e_o

From the analyses above, the order of priority to an unknown is decided as mentioned above as follows.

M, W > k, e, I > a ; w, f, fixed.

Parameters to be Determined with Few GCPs
The examinations were performed using simulation data and LAC ( Local Area Coverage ) data in order to decide which parameter should be determined with few GCPS. In case of simulation data, both ground and image coordinates of GCPs had no errors and the inclinations of satellite attitude were none. This case showed the theoretical adoptability of this system. In case of LAC data, there were probably some errors of coordinates and some inclinations of attitude. This case.

Showed the practical adoptability. The selection of examination case, or the selection of parameters to be unknowns, carried out with respect to the result mentioned above. The estimation was made by the residuals of check points.

Table 3 shows the result. In case of simulation data, the higher the order of polynomial is, the higher the accuracy is. Otherwise. This seems to result from the error of coordinates of GCPs. The order of priority of parameters to be unknowns in section 3 are reasonable except semi-major axis (A). This sees to result from the correlation between parameters, because A are not so correlated with the others. From the examination, the parameters to be unknowns are decided with respect to the number of GCPs as follows. The eccentricity (eo) is adopted only over the area scanned near from the perigee or the apogee.

Conclusions
The system which the orbital elements and the attitude of the satellite can be corrected has been developed by utilizing co linearity condition in photogrammetry. The system has become adaptable to the case of few GCPs through the examination which orientation parameter should be corrected.

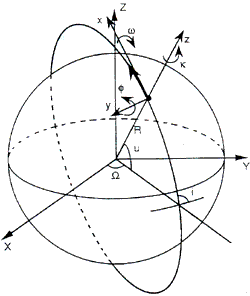
Fig 1Satellite Orbit and Colinearity Condition
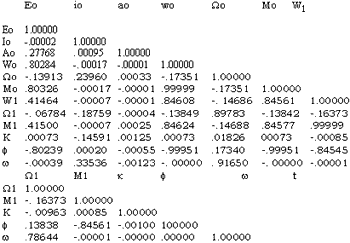
Table 1 Correlation Coefficients Table between Parameters

Table 2 Variations of Parameters and their effects on Residuals

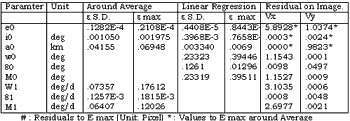
Table Number of Unknown Parameters VS. Residuals

NumberOf GCPs	Number of Unknown	Simulation Data		Lac Data
NumberOf GCPs	M W i e a k	V x	v y	v x	v y
0	System Correction	44.7522	1.76706	17.2960	6.65532
2	2 1 0 0 0 0 1 2 0 0 0 0	.10481 .14931	.07820	1.60889	4.96519
3	2 2 1 0 0 0 2 2 0 0 0 1 2 1 1 0 0 1 2 1 0 0 1 1 2 1 0 1 0 1	.02084 .00858 .01061 .01027 .00661	.7768 .02494 .02287 .04642 .04800	1.26535 1.29031 1.29865 1.26385 1.43866	4.19561 4.20818 4.14881 .80799 1.79665
4	2 2 1 1 0 1 2 2 0 1 1 1 2 2 1 0 1 1 2 1 1 1 1 1 2 1 1 0 1 2 2 1 1 1 0 2	.00060 .00485 .00471 .00031 .02148 .00245	.00189 .01560 .01510 .00074 .01703 .00173	1.47055 1.42514 1.36451 1.42512 1.03808 .86861	1.56004 1.18892 .88091 1.18946 .84640 1.80222
5	2 2 1 1 1 1 2 2 1 1 1 2 3 2 1 2 0 1 3 2 2 1 0 1 3 2 1 0 1 2 3 2 1 10 2 3 2 1 1 1 1	.00028 .00023 .00008 .00136 .00046 .00025 .00030	.00116 .00118 .00017 .00209 .01859 .00144 .00116	1.06253 .99626 1.22994 *** .90160 .85707 1.08385	.80074 .65560 1.14388 *** .65726 .96612 .65531
6	2 2 1 1 1 1 2 2 1 1 1 2 3 2 1 1 1 2 3 2 1 0 1 2 3 2 1 2 1 2 3 2 2 2 1 1 3 2 1 2 1 1	.00017 .00021 .00017 .00048 .00007 .00008 .00006	.00085 .00083 .00084 .01895 .00008 .00016 .00009	1.14459 1.01355 .97795 .93080 1.11878 * *	.86769 .65990 .66246 .69257 1.63027 * *
7	2 2 1 1 1 1 2 2 1 1 1 2 3 2 1 1 1 1 3 2 1 0 1 2 3 2 1 2 1 1 3 2 1 1 1 2 3 2 1 2 1 2	.00027 .00022 .00026 .06012 .00007 .00019 .00007	.00107 .00109 .00107 .01521 .00009 .00109 .00008	* .84116 * .73266 8.38219 .79345 1.79084	* .64648 * .70250 2.07203 .65265 1.52381

(***: not calculated or very big residual), (Unit: Pixel)