Fuzzy pixel decomposition approach in classification of Remote Sensing data

Fuzzy pixel decomposition approach in classification of Remote Sensing data

Tsukasa Hosomura, Pan Rui
Computer Science Division
Asian Institute of Technology
G.P.O. Box 2754, Bangkok 10501, Thailand

Abstract
In the conventional remote sensing classification, most classification results are represented in a one-pixel-one-class mapping in which a pixel is a indivisible minimum unit no matter whether it is class mixture pixel or not, which greatly and always limits the improvement of classification and boundary accuracies.

This work describes a new approach of using fuzzy pixel decomposition algorithm in which each pixel is represented as a fuzzy pixel and then divided into sub-pixels. The algorithm consists of two major steps: Pixel membership grade analysis, and Pixel decomposition, in which fuzzy set theory is applied for identifying the land cover membership grade of each pixel, and neighborhood window is used for identifying the position of each sub-pixel. The identification and positioning of each sub-pixel improve the extraction of spectral information and then achieve higher classification and boundary accuracies.

Results of classifying TM and MOS-1 images of Thailand are presented and their accuracies are analyzed.

I. Introduction
In land use classification, the purpose is to produce thematic map which is essential for many planning activities. Many image classification methods have been used during the past several decades with quite different approaches. However, almost all of these methods treat a pixel as a minimum unit and classify each pixel into one of the predefined classes, moreover, the mixture pixels are also unexpectedly classified into one of the likelihood class, which results in low classification accuracy. Therefore treating pixel as minimum unit in classification is one of the major shortcoming that sharply and always draws down the classification accuracy.

Some of analysis work has been done in this field. One method that uses linear spectral mixing analysis has succeed in display fraction image for endmember (class) which is obtained by solving equations deriving from number of bands and predefined spectral values from laboratory. Unfortunately the limitation is that the number of endmembers should not exceed the number of spectral bands. Fuzzy set theory provides useful concepts and tools to deal with imprecise information. A method using probability measures of fuzzy event to calculate membership grade for pixels has used, which cause the identification of a pixel component cover class. Other works related to fuzzy application in classification are the fuzzy logic, in which a rule-based classification system for images is presented.

Though these works have applied different approaches in analysis for pixel component of land cover in classification, it is still need a method to dissolve the class mixture pixel in image and to produce a better classified map with higher boundary accuracy which is useful in application.

This work tries to explore a new approach, that is fuzzy pixel decomposition algorithm, to break mixture pixel into small pixels (sub-pixel) using fuzzy set theory for pixel membership analysis, which is introduced in section II, and then position these sub-pixels which is introduced in section, III, so that to achieve a higheroduced in section, III, so that to achieve a higher boundary accuracy map and high classification accuracy. Up till now, part of results have shown that this approach has achieved a higher results of classification and boundary accuracy, which is listed in section IV, however it still needs more improvement and modification.

II. Pixel Membership Grade Analysis
For pixel is no longer treated as minimum unit, therefore a pixel content will be represented as fuzzy pixel with a attachment of membership function based on the Euclidian distance defined as:

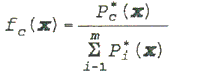
Where

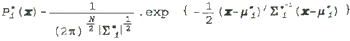
N is the dimension of the pixel vectors, m is the number of predefined classes, and i=1,..., m, x is the pixel vector.

Here a higher accurate mean and variance vector are needed for correctly calculating membership function, which will directly affect the accuracy of classification. Low classification accuracy is largely due to the variations between statistically generated vector and the "real" ones possibly from laboratory. Tests have verified that a membership grade calculated from above formula is proportional to the percentage to which the pixel contains a given type of land cover. Mixed pixels can be well identified by analyzing the membership grades.

III. Pixel Decomposition into Sub-Pixel
Based on the above work, a original pixel then can be represented by smaller pixels called sub-pixels (according to fuzzy set theory, subjective category is decomposed into two smaller subjective categories, each of which needs fewer descriptors to be completely described. This process of decomposition could be continued until the descriptions of the subjective categories generated are reasonably defined). In this work, a pixel is divided into 9 sub-pixels, and the number of sub-pixels containing only one class component can be calculated using membership function as follow.

N_c- [ f_c (X_j). 9+ 0.5]

X_j is a pixel measurement vector, j = 1,..,.n.
N_c is the number of the sub-pixel in class k.
n is the number of pixels in a image.
f_c is membership grade function.

Here we can say that if all the pixels have been divided into sub-pixels with "pure" class cover component replaced, then there is no "fuzzy" pixels existed in that new image, in other words, it implies that the accuracy is improved if these sub-pixel can be properly positioned.

Based on the principal of general homogeneous of the pixels and distribution in a image, especially in the rural area such as CHIANGMENI, the sub-pixel position can be well defined and positioned at the right position.

The positioning algorithm which is used in this work is by applying a 3x3 window over a classified map produced by maximum likelihood algorithm that moved across the map in 3 sub-pixel jumps, and performed a homogeneous fit in 4 directions: horizontal, vertical and both diagonals, but retained only the central 3x3 sub-pixel for balancing.

The positioning of each sub-pixel is the most important step in pixel decomposition algorithm, the efficiency of correctly positioning the sub-pixel is directly affected the classification accuracy and boundary accuracy even though the number of sub-pixel with class cover is correct.

IV. Testing of Pixel Decomposition Algorithm
The current part results have proved that the pixel decomposition algorithm has a better boundary accuracy and classification accuracy, but not so much. Further improvement and modification of the algorithm will be done in later work as well as test method.

The number of error boundary pixel both for maximum likelihood and fuzzy pixel decomposition algorithms is listed below, the test area is the whole image scene (240x240) cut from MOS-1 image with large homogeneous land cover (forest and shadow). Average sampling one pixel form 9 pixels, a sub-scene of 80x80 in pixel size is used for both algorithms, the enlarged map produced by MXL and map. Produced by pixel decomposition are compared. The result has shown the improvement along boundary.

CLASS	0	1	2	3
MXL	8298	3117	10521	298
PIXEL DEC.	7611	2515	7754	166

The Number of Error Pixels for each Algorithm
The overall accuracy is 80% for MXL and 85.5% for pixel decomposition. Some other tests also shows that the algorithm is favor to some class cover.

V. Discussion and Conclusion
Fuzzy pixel decomposition algorithm is a try to dissolve pixel component, and it has found that correctly decomposition and positioning are the most important steps which is also very sensitive to the specific image, while as a tool for post-processing, it is still worth of doing. However, it can be concluded from this study that fuzzy pixel decomposition is a valuable tool for the boundary enhancement of certain land-cover. Further work will be continuing to achieve better results.

Acknowledgment
The authors wish to thank Mr. Kazuo Joko, Director for Co-research and Coordination in Bangkok, National Space Development Agency of Japan and the National Research Council of Thailand for providing the raw images and for the assistance provided.