A Solid angle based coordinate system for global GIS

A Solid angle based coordinate system for global GIS

Koji Kajiwara
Institute of Industrial Science, University of Tokyo
7-22-1, Roppongi, Minato-ku, Tokyo, 106
Japan

Abstract
An equal-area projected raster image format for the global database, which can be the main source of Global Geographic Information System (GGIS), was discussed. Equal solid angle projection method, which is similar to the sinusoidal projection, is proposed to construct a global data in raster image format. In this paper, a way of constructing the image and the result of estimation of area error are described.

1. Introduction
For the Earth surface monitoring, construction of Global Geographic Information System (GGIS) which includes global database has been required. The database should include many sort of data such as terrain model, land and sea surface temperature, precipitation, various kind of indices like vegetation index, satellite data and etc. Currently, some raster type global data which can be source of global database are existed, and most of them select plate carree (longitude/latitude) projection. The plate carree projected data can be treated easily as simple digital imagery which described in column and row. When we use the data, it is enough to simply copy each pixel from outer storage devices into 2 dimensional array of computer memory. In the projection, however, pixels in mid or high latitude region have a large area distortion, in other words, plate carree projected data are variable area scale data. Considering the use of the data in GGIS, any data format includes a large area distortion can not be considered as a suitable database for global level analysis.

In this paper, equal solid angle projection for global data which is similar to sinusoidal projection was proposed. In section 2, basic concept of this projection method is described. In following section, results of area error estimation on several resolutions are shown. Finally, in the section 4, advantages and disadvantages of this projection are discussed.

2. Basic concept of equal solid angle projection
Under the assumption that the earth is perfect sphere, considering it is covered within of infinitely small surface do, that area is described as,

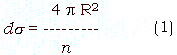
where R is the radius of the earth. ds located at latitude q and longitude j also can be written with solid angle m which corresponds to ds;

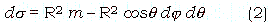
Since ds is fixed after determination of area scale n, dj can not be equal to dq on deferent latitude q if we consider the figure of small surface piece as rectangle. Although it can be consider that some kids of polygons which area correspond to ds , in the case, we must abandon the benefit of longitude/latitude coordinate system. The benefit is, adopting the rectangle figure case, we can make image line to be corresponded to a latitude band, which leads to an easy handling of the projected data. Additionally, almost existing global data sets use the plate carree or cylindrical projections. Considering the conversion of format from these data, it is favorable to adopt the rectangle figure which is delineated by longitude line and latitude line.

Figure 1. Area error of pixels on different latitude. (a) Using round off for calculating equation (6). (b) Using trancation.
After deciding the figure of infinitely small surface, there are two choices on dividing scheme of longitude and latitude. They are 1) Fix dj (divide longitude equally) and change dq , 2) Fix dq (divide latitude equally) and change dj. The former is correspond to cylindrical equal-area projection and the later is correspond to sinusoidal projection. In this paper, the later one was selected and the reason was it's less distance distortion along longitude and latitude line rather than the former one.

Utilizing this projection for digital imagery, each line which corresponds to latitude band has different number of pixels. Here, define that dq and dj equal to dh at the equator (q = 0), the number of pixels NLT(q) is described as;

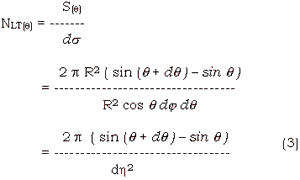
and longitude width w of a pixel on latitude q is given by

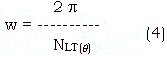
Generally, NLT(q) is not on integer value. According, all the pixels have truncation or round off error of area, and the magnitude of error is different on different latitude band. Then the area covered with one pixel on certain latitude band ds(q) can be written as;

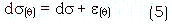
where e is area error of one pixel on latitude q

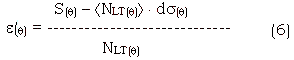
Where á ñ means round or truncation.

3. Error estimation
As mentioned in above section, in strictly sence, digital imagery by equal solid angle projection does not actualize equal area. In this section, the results of error calculation are described.

In order to clarify the error of each pixel on different latitude, the ratios of e and ds(e(q)/ds) were calculated in 3 resolution which are dh = 30', 15', 5'. Figure 1 (a) shows the results using round to calculate e(q) and figure 1 (b) shows the results using truncation. As shown in these figures, (e(q) / ds) is lower than 0.5% in both cases except the polar region which exceed 800. These results indicate that the equal solid angle projection can be regarded as an equal-area projection except for the case of focusing northern Greenland or Antarctica.

4. Discussion
The advantages of the equal solid angle projected global data are;

1) Except polar region, pixels in the data contained only a very small area distortion. Accordingly, in many cases, area calculation of certain region can be replaced with pixel counting. Considering the characteristics of global database, each pixel should have a certain kind of attribute such as elevation, temperature, land cover, etc. When we refer these data, it is a favorable factor to use the information which represent the same areas.

2) The data have no redundancy. Although each pixel have some area distortion, they don't overwrap each other and total represented area of whole pixels is equal to area of the earth surface. Comparing the data capacity to the plate carree projected data which have same single resolution on the equator, equal solid angle projection data have only about 64% ( = 4p/2p2 ) capacity.

Simultaneously, the data have following disadvantages;

3) Each latitude band has different number of pixels. That is, record length of each line is different. If we want to know the position of a pixel in the data file, we must do a relatively complicated calculation rater than the data projected by plate carree or other cylindrical projection. Although we can avoid these calculation by using the line position table, in this case, extra capacity of memory or outer storage devices are required.

4) On the large scale projection such as dh = 50, it can not be regarded as equal area projection for large area distortion.

Acknowledgements
The author thankful to Mr. Hiroshi Okumura and Mr. L.K. Perera, Remote Sensing and Image Research center, Chiba University, for their assistance.

Reference

John P. Snyder, 1987, "Map Projections - A Working Manual", U.S. Geological Survey Professional Paper 1395, United States Government Printing Office, Washington.