| GISdevelopment.net ---> AARS ---> ACRS 1992 ---> Poster Session P |
Estimating Leaf-Area Index of
a Crown Canopy in a Pecan Orchard
Li Xiaowen Wang Jindi, Zhu
Chongguang, Liu Yi
Institute of Remote Sensing Application, Chinese Academy of Sciences Beijing 100101, P.R. China
Alan H. Strahler
Certer for Remote Sensing, Boston University , Boston, MA 02215, USA
Institute of Remote Sensing Application, Chinese Academy of Sciences Beijing 100101, P.R. China
Alan H. Strahler
Certer for Remote Sensing, Boston University , Boston, MA 02215, USA
Introduction
The advance of remote sensing science and technology has provided new airborne or satellite sensors able to sense the reflectance of a ground target at different directions, which brings once again the anisotropic reflectance characteristics of earth surface to attention of researchers. Many model have been proposed to relate the geometrical and biological parameters of various ground target to directional reflectance data acquired from a remote sensor, although their application and accuracy need large amounts of accurate measurement for model is an essential part in both geometric-optical models and rediative transfer theory.
Pgap is the probability that a photon incident upon a vegetation canopy will pass directly through the canopy without being intercepted by a leaf, branch, or stem. It is thus a function of these structural parameters as well as the pathelength within the canopy. A recent field experiment (MAC-VI) presented the opportunity to relate gap probability to detailed between-crown information on the size, shape and spacing of individual tree crowns as well as within-crown information on leaf size pecan trees in an orchard near Phoenix, Arizona. The experiment was jointly sponsored by the Canada Center for Remote Sensing (CCRS), Ottawa, and the USDA Water Conservation Laboratory, Phoenix. The tree measurement was designed and carried out by CCRS personnel, with three of authors providing additional help. Our own data collection was to measure the gap probability by photogrammetric methods [1].
It turned out that measuring leaf area index (LAI), leaf angle distribution (LAD) and crown structure in the field was very difficulty and manual – labor intensive, and the large volume of measured data is not easy to handle, either . At this writing , we have not received all planned field data from the collaborating team at the CCRS. In such circumstances, we have explored the results for a few photos of one of the pecan trees to extract crown information by combining computed tomography and a crown Pgap model. Though the reconstructed crown parameters still await confirmation, the initial result are reasonable and encouraging. With further development and validation, this technique may have wide application in the future field experiments of forest remote sensing.
This article summarized our tree tomography method to reconstruct crown shape and further estimate LAI, as well as to demonstrate its practicability and rationale. Though further improvements are still needed, our method provides a sound basis for a new approach to data acquisition in forests.
Computed Tomography and Estimation of LAI
Theoretically [2] , computed tomography (CT) can be applied in any reconstruction problem if the signal received by a single detector can be expressed as linear integral along the ray path penetrating the object F(x,y,z)
Usually, we obtain an array of Po values and call it a projection Po(u,v). If in such a projection, all rays reaching detectors (u,v) are parallel, it is termed a parallel – beam projection. Frequently, we have a fan – beam projection [3]3, in which the rays reaching different detectors are not parallel, but converge to a certain point given 0 and the optical geometry. Various algorithms can be used to reconstruct f(x,y,z(, given enough number of projections at a sufficiently wide range of directions.
Typical models for gap probability in a volume cell of leaf canopy along the ray paths are of the form.
where L is the total single – sided leaf area within a unit volume cell, k (0) is the fraction of the foliage area projected toward the angle of incidence, s is the pathlength of the ray beam through the uniform canopy, and 0 is the zenith angle of incidence [4].
Taking the logarithm of both sides of (2), and allowing changes in the foliage volume de3nsity L, we have:
It is obvious that reconstruction of a 3-D LAI distribution L(x, y, x) from Pgap measurements can be posed as a typical CT problem.
Among many CT algorithms, we selected back – projection because of its flexibility and simplicity. A simplified example shows how this algorithm works. Assuming 2-D object f (x, y) contains 2*2 cell as follows:
Then by (1) we can obtain a horizontal projection (9,11), a vertical projection (8,12), and two 45 degree projections, (2,13,4) and (5,7,8) respectively. Obviously we can solve for f(x,y) by selecting four independent equations. However, when f(x,y) involves hundreds by hundreds of cells, it will be much easier to equally distribute the sums along back projection paths and average all back projections.
First, we back project the vertical projection, and the horizontal, ... it will result the following:
| 4 | 6 | 805 | 10.5 | 15 | 14.5 | 20 | 18 | |
| 4 | 6 | 9.5 | 11.5 | 12.5 | 18 | 16 | 26 |
Then averaging by total number of back projection for each cell, we obtain
This is close to the original f(x,y) but there are notable errors. The reason is that there is a “quasi-bone” element ( the value 8 is much larger than surrounding ones ) and the projection is unfiltered. However, the more projections we have, the less sudden the change in f(x,y), and the more accurate the algorithm will be.
Date Acquisition and Image Processing
To measure the gap probability, we collected upward-looking ground photography in the pecan orchard using a blue-filtered Wide 35-mm panoramic camera with a 135 – degree-wide field of view. The resulting photographs were of very high contrast, providing easy and accurate separating of sky and canopy. Then the photos were scanned and digitized for computation of probability as a function of location within the orchard and direction of view [1].
Four trees were identified as targets. These were the same trees selected by CCRS personnel for detailed measurements of leaf and canopy structure. Camera stations were laid out along three lines ranging out from each tree. One line assumed the row direction, while the other two were at 60 degree angle to it . Along each leg, the upward-looking camera was placed at distances 0.5, 1.5,... meters from the tree. The long axis of the camera was oriented orthogonally to the grid line. The entire data consisted of 14 36-exposure rolls of film.
Contact print sheets (8” by 10” ) were made for each roll, and the sheets were then scanned with a C4500 film scanner at 50 micron resolution, producing images of 4,000 by 4,200 or 4, 600 pixels. Within this image, each photo occupies an image of 480 samples by 1, 160 lines. The separation of sky and canopy is obvious and unequivocal, and each pixel can be easily labeled as gap or canopy.
In order to estimate gap probability, we applied a low-pass filter to the image using a 20 by 20 pixel window. This filter produces a simplicity angular resolution of 2.30 by 2.30 in the centerline of the photo. From the line and sample photo. From the line and sample coordinate of each pixel, the associated view zenith angle may be easily calculated. At the corners of the photo, the view zenith angle approaches 700
With these Pgap measurements available, as mentioned above, the reconstruction of L( x,y,z) can be posed as a typical CT problem. However, there are also some special problems in CT reconstruction of a tree crown. For example, trunk and branch are opaque to sky light, similar to bones in an X-ray CT. The problem caused by the trunk can be taking multiple picture around it, hence it will not cast a permanent shadow in reconstruction. Branches present a more difficult problem, especially when they are high above the ground or very closed to dense foliage, because it is unlikely that enough projection can be obtained around them.
Our back project algorithm hence was specially designed to deal with these practical difficulties. It has the following steps:
a) Using conventional back projection to reconstruct the 3-D envelope of foliages, In this step, only “gap paths” play significant roles,
b) Identifying all “good – paths” which pass through foliage envelopes without hitting trunk or branch. A trunk / branch volume element is identified if all paths through it are zore - Pgap. A “good-path” is defined as a path that never touches a trunk / branch element.
c) Using all “godd-path”, obtaining some statistics such as mean K (0) . This is done by sorting all good paths into groups with approximately the same pathlength and zenith angle and analyzing the difference in Pgap- pathlength relations between different equal – zenith groups.
d) Back-projecting all “good path” LAI into the foliage envelope. Then we obtain the 3-D distribution of L(x,y,z):
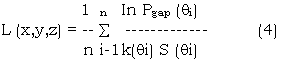
where n is the total number of “good paths” passing through volume element (x,y,z), S(qi) is the path length of the ith path within the envelope.
In short, when we have a good Pgap measurement we assume the corresponding leaf area is equal – likely distributed in the volume where the fan-beam intersects the foliage envelope. The more ‘good path” projections are available, the closer the result will be to thetruth. Knowing L(x,y,z) and crown envelope, it is easy to calculate the total LAI.
Fig 1 The resulted reconstruction of the crown envelope, from (a) to (h) present as slices of crown at 3m to 10m respectively
Fig 2. The L(x,y,z) distribution, from (a) to (f) present as slices of crown at 3m to 8m, respectively.
The resulted reconstruction of the crown envelope is shown in fig. 1, present as slices of crown at 3,4,... to 10m respectively. Since at 2,4,... to 10m respectively. Since the experiment was designed to validate Pgap model, and photo were taken along three legs 60 degree apart, at the most only half of the crown can be reconstructed.
Fig. 2 shows the L (x,y,z) distribution also as slices at 3 – 8m, where gray values are proportional to L-values. The total LAI estimate of the half – crown is 3.4644, and the widest radius at one direction is 3.8m at height 5m, while the widest radius on the other direction is 2.5m at the height 4m. All these are quite reasonable and agree with our observations in the field.
Discussion and Conclusion
Our result is encouraging, it shows the potential of tree tomography to measure crown parameters in an effort - effective way. However, there are several important issues need to be addressed for further developing such methods.
1) A key for successful reconstruction using back projection is enough overlap of coverage of fan beam back projections of “good paths”. However, ;because the experiment was designed for another purpose, the overlap is not enough in this work, especially at the height under 3m, Meanwhile, above 7m, the coverage of “gap paths” is not sufficient , hence the envelop below 3m and above 8m are not reliable and the tree height is overestimated (10m). In future work, we suggest either to increase the overlap in photo coverage or to make some basic field measurements such as tree height, trunk DBH, crown width, etc., so that the algorithm can concentrate on estimate of only those parameters which are difficult to measure in filed, such as LAI and LAD.
2) It is difficult to identify branch elements by using blue-filtered imagery only, since dense foliage and branches can’t be reliably distinguished. Since leaves have much higher transmittance in NIR band, color infrared photos will be preferred to B/W ones.
3) The posture of the camera should be better controlled or at least better recorded. Because of the uncertainity of camera posture, when we tried to identify branch elements a the height 5m, where the overlap of back projection is near the best, we could not use all backprojections – when we used more than 3, the branch elements disappeared rapidly. Because of this problem in branch identification, we had to discard those paths of low Pgap in our statistical analysis. After these good paths were further divided into zenith angle groups, many groups didn’t have enough good paths. Thus, though the results shown little difference among zenith groups which had sufficient numbers of good paths, and we have therefore assumed that LAD is spherically uniform and K(0) = 0.5, the evolution of K(0) and LAD need further support from new experiments.
4) The lack of coverage on the other half of crown is of course obvious. This yields some uncertainity of the crown envelop and then degrades the reliability of LAI estimation. In future work, full coverage of crown will be necessary. Even though many improvements are needed, based on our algorithm development and initial reconstruction results so far, we can conclude that our tree tomography approach is sound in theory and promising in future application for forest data acquisition.
Acknowledgement
This research was supported in part by NASA grant NAGW-2082, U.S. NSF grant INT-9014263, and Chinese NSF grant 4880050
Literature Cited
- A.H. Strahler, X. Li, A. Moody and Y. Liu, “Gap probability: Measurementsand models of a pecan orchard, IGARSS proceedings, 1992, p. 760-762.
- Herman, G.T., “Image reconstruction from projection: The fundamentals of computerized tomography,” Academic Press Inc., 1980.
- Gallery, G.T., “The reconstruction of fan-beam data by filtering the back projection,” Computer Graphics Image Processing 10, pp. 30-30 – 47, 1979.
- Li, X., and Strahler. A.H., “Modeling the gap probability of discontinuous vegetation canopy, IEEE Trans. on Geoscience and Remote Sensing , 26:161-170, 1988.