| GISdevelopment.net ---> AARS ---> ACRS 1992 ---> Poster Session P |
The algorithm converting 2DRE
quadtree to vector
Xiao Ke
Institute of Remote Sensing Application Chinese Academy of Sciences
P.O. Box 775, Beijing 100101, P.R., China
Institute of Remote Sensing Application Chinese Academy of Sciences
P.O. Box 775, Beijing 100101, P.R., China
Abstract
This paper advances and analyses an algorithm converting 2DRE quadtree to vector in order to extract the boundarys of fields in an image in its 2DRE quadtree format. The boundarys of fields in images are represented in the form of coordinates of the ends of vectors for displaying the fields’ shape and outputting the vectors easily. In this paper, the base of the algorithm is introduced first; then the algorithm is described in detail; finally the features and the complexities of time and space of the algorithm is estimated and analyzed.
In the work of remote sensing image processing and geographic information system, the conversion between different data structures is an important and interesting topic. Quadtrees, especially 2DRE quadtree have a lot of advantages such as regularity, flexibility, saving space of storage and the property easy to represent structural information of images while chain code-vector is the data structure used to detect and describe the boundaries and shapes of fields in an image. Both of the two structures have their own advantages and disadvantages in different situations and suit different uses in practice. In a completed image processing system or geographic information system there should be some data structures and flexible conversions between them for their corresponding uses So the research on the algorithm converting the two data structures is significant.
1. Field’ boundarys and chain code
Given a field in an image, its boundary can be served as a graphical polygon or a closed curve. So a format representing it can be defined.
As Fig. 1 showing, i = 1,234, 4 represent four directions of 90° * i, clockwise respectively. So a curve on a plane can be described with a series of connected unit vectors, then the boundary of a field as a closed curve can also be rep- resented in this way. The sequence of vectors is called “chain Code” [1].
Fig. 2 shows a field in an image; Table 1 is the chain codes representing the boundary of the field from point. A. It can be seen that the shape for the boundary and the bmp and crank features of the curve are displayed by a series o numbers very clearly.
Fig 1 Rule of direction codes
Fig 2. A field in an image
Table 1 The Chain Code of the Field’s boundary in Fig. 2
| 0 | 3 | 0 | 1 | 0 | 3 | 0 | 3 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| 3 | 2 | 1 | 1 | 1 | 0 | 1 | 2 | 2 | 2 |
| 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 0 | 3 |
2. Boundary Tracking
Suppose there is a 2DRE quadtree representing an image in which the elements are the contiguous areas of points with value ‘1’ . The “field” is composed of these kind of contiguous areas. Based on the discussion in last section, from any point on the boundary, according to the directions of a series of unit vectors, the chin codes of the boundary can be determined. The last vector must point at the initial point since the curve is closed. So if the initial point and the sequence of vectors and given, the shape and the position are also be determined. Again, since the curve is closed, any point on the boundary can be treated as the initial point. For convenience, the first element is chosen as the initial point. The reason is: first, it is definitely on the boundary of the first, it is definitely on the boundary of the field; second, it is located at upleft corner ( not necessarily upmost or leftmost, as the situation of smooth curve in mathematics ). So the initial tracking direction will be defined easily.
Before tracking procedure, the initial point pair ( P1,1, P1,0) should be given where P1.1 is the point in the field and P1.0is background point. As mentioned above, the point represented by the first element in quadtree is served as P1,1, and because it is located at upleft corner of the field, the initial direction is determined as 0. So, the relation between P1,0and P1,1 is
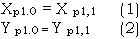
After the initial point pair ( P1,1, P1,0) and initial direction 0 are given, the next point pair and direction can be found according to the quadtree data. Searching in this way one by one, the tracking procedure for the boundary of the field is realized . It is known that the field is realized. It is known that the vectors describing the boundary curve have four directions, so if a point pair (Pi,1,Pi,0) and direction Di are known and next point pair (Pi+1,1, Pi+1,0) and direction Di+1 are required , the situations will be showed as Fig. 3 without any exception ( forward in the direction of clockwise, so the field is always in the right of forward direction)
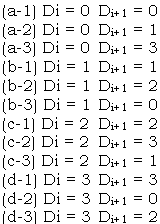
Fig. 3. Possible Situations of Boundary Tracking
Fig. 3 Possible Situations of Boundary Tracking From fig. 3, it can be known that no matter the direction is 0,1,2, or 3, the possible next direction has only three situations, i.e. forward, left and right which can be presented in formulas below:
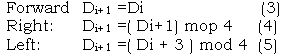
the relation between the coordinates of point pair in different directions are showed as below:
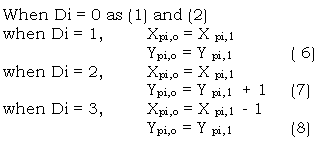
So based on the regulations showed in (6) – (8) , tracking procedure long the boundary can be done, then the whole boundary curve would be obtained. In the tracking, one has to detect the point pari ( pi,1, pi, o) often to determine the orientation of the curve and detect if return to the initial point to decide if the tracking should be finished. Since the field is given by 2DRE qadtree, the conversions of “code to coordinate” and “coordinate to code” [2] are needed for the detecting in the procedure and the determining of next point pair. the former is used to obtain point pair to record; the latter is used to get quadtree code to determine if the point newly obtained is field point or background point. There is another use of the detecting, i.e. when there are more than one field in the image, the tracking procedure will be needed more than once. it is known, according to the structure of 2DRE quadtree, that if the number of tracking is less than the number of fields in the image, there must be some elements as code contiguous area not visited in quadtree. So through the detecting, the number of visited field can be recorded in a table. After every tracking finished, the table will be searched. if there is no field with the least number to determine the boundary of next field. so the possible missing of fields will be avoided.
3. The Description of The Algorithm
Q-V converting algorithm is used to obtain the boundary of fields in images from their 2DRE quadtree file. In the algorithm, the X, Y coordinates of the points at the boundary are recorded to symbolize it instead of chain code in order to merge the points on same lines (00, 450, 900, 1350). Only the coordinates of the two end points on the end points on the same line are recorded rather than every points. Not only is this way used to save graphic later on.
The operation procedure of using the algorithms to get boundary curves of fields in image is described below with an example 2DRE Quadtree file (Table 2) and image it represents (Fig. 4)
1) Get the “base Code Table” according to formulas (3)-(10) in [2].
| Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Quadtree | 1 | 9 | 11 | 17 | 19 | 26 | 36 | 48 |
| Code | 1 | 1 | 5 | 1 | 5 | 1 | 4 | 16 |
Fig. 4 the Image Represented by The Quadtree in Table 2
2) ISB < --0; number of initial field K <--1.
3) Point NP <-0, which points at the vector area IBOD.
4) Use B (K, 1) as the initial point AIN; Q1 = AIN;
5) Get the X, Y coordinates of AIN, according to (1), (2) and (11)-(14) in [2].
6) Obtain X0, Y0 from X1, Y1 and the direction code ISB.
7) Obtain Q0 from X0, Y0 and “Base Code Table”. Then all information of initial point pair (p1,1,P1,0), i.e. their quadtree code and X, Y coordinates, have been ready in use. (Table 3).
8) IBOD (NP, 2) <--X1, IBOD (NP,2) <- Y1, then NP <- NP+1.
9) Put ‘1’ into the Kth position of field number recording table.
10) Track the boundary of the field, based on ISB and point pari, first, get the new point pair X’ 1, Y’1, X’2, Y’0 along ISB and their quadtree Q’1, Q’0, then check if it is legal. if ‘Yes’, record X1, Y1; then check which area in B the Q belong to; record the area number; X1 <--X’1,
Y1 <-- Y’1, X0 <--X’0, Y0<--Y’0, Q1<-- Q’1. Q0 <-- Q’0, get the new ISB and the information about the new point pair to replace the old one. If ‘No’, adjust ISB and point pairinformation, repeat the procedure above until legal point pair is found.
11) Check if NP> 4. If ‘Yes’, decide it the points in the newest IBOD are needed merging. If needed, change the content in IBOD, thenNP <-- NP-1; otherwise goto next step. (Table 4 and Table 5 show the content in IBOD before and after merging, respectively)
12) check if present Q1 = AIN. IF ‘Yes’, this round of tracking infinished, put sigh in IBOD (five ‘0’s, showing in Table 6). If ‘No], goto 10) . (Table 7 shows the content in in IBOD after first round of tracking )
13)Check field number recording table, get the flag IB and the leastnumber of the area non-visited, KF. (Table 8 shows the field nunberrecording table )
14) Check if IV = 0.’0’ means all fields are visited, goto 17). ‘1’ , goto next.
15) Check elements in KFth field in B, see if there is a point having the property of boundary point ( It must have at least one neighbour point in background, i.e. not in B). If no boundary point is found, put ‘1’ in KFth position in “field number recording table’, goto 13).
16) AIN<-- Q,; goto 5). (Table 9 shows the initial point round of tracking )
17) Put five ‘0’s in IBOD, finish the whole procedure tracking. (The final result and the content of field number recording table are showed in Table 10 and Table 11 respectively )
| Q1 | X1 | Y1 | Q0 | X0 | X0 |
| 3 | 1 | 1 | 1 | 1 | 0 |
Table 4 Chain code Area before Same Line Mering when tracking at point A in the image
| X | 1 | 1 | 2 | 3 |
| Y | 1 | 2 | 2 | 2 |
Table 5 Chain code Area after Same Line Mering when Tracking at point A in the image.
| X | 1 | 1 | 3 |
| Y | 1 | 2 | 2 |
Table 6 Field Number Recording Table when Tracking at Point A in the image
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Table 7 The content of Chain Code Area after First Round of Tracking
| 1 | 1 | 3 | 3 | 4 | 4 | 7 | 7 | 4 | 4 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 2 | 3 | 3 | 4 | 4 | 7 | 7 | 5 | 5 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 0 |
Table 8 The content of field Number Recording Table
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| Q1 | X1 | Y1 | Q0 | X0 | X0 |
| 17 | 5 | 0 | -1 | 5 | -1 |
Note: In the algorithm, Points outside the image (X or Y> 2n- 1; X or Y<0 ) are defined as ‘-1’,
11334477442211000005775500000
12233447744331000000011000000
Table 11 Final Field Number Recording Table
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Discussion
Q-V algorithm goes through a series of tracking procedures to get the sequence of X,Y coordinates of bundary curve of fields in image represented in 2DRE quadtree. It mainly has two features: The first, it is convenient to use. The algorithm can be operated directly on 2DRE quadtree, which is a simple, storage saving data structure for images, without the complicated converting procedure of quadtree to raster, then raster to vector. Especially when users want to have a series of set operations, such as union, intersection, complement and difference on an image and hope to see the results, e.g. shape or other features of the fields in the image after every step, it they sue the algorithm directly, it must be much convenient and much simpler than they use vector to raster and raster to vector conversion in sever step.
The second, It saves time and space. The algorithm obtains field’s boundary directly from quadtree, so the space is only the quadtree file and chain code area ( to record X, Y coordinates of boundary curve). It dose not need the big matrix space for raster image data; in addition, boundary tracking deals with only the points on the boundary curve rather than all points in the image, so the operation time is also short, especially in the situation that the fields are big the rate of perimeter and area of the fields are small. In programming of the algorithm, some measures are taken to save more some measures are taken to save more time and space to make it more effective, e.g. use bits to records information than bytes or integers to compress this part of space least; according to different situations, the alogrithm can decide when use sequential searching or binary searching to save time.
References:
- A. Rosenfeld, A.C. Kak, Digital Picture Processing, Academic Press, 1976.
- K. Xiao, The Algorithm Converting Raster to 2DRE Quadtree, The Proceedings of Second International Conference on Automation, Robotic and Computer Vision, Singapore, September, 1992.