Geometric Correction of NOAA AVHRR GAC Data

Geometric Correction of NOAA AVHRR GAC Data

Kimiaki Saitoh*, Toshiaki Hashimoto** , Koji Kajiwara* and Ryutaro Tateishi*
Center for Environmental Remote Sensing(CEReS), Chiba University, Japan
1-33, Yayoi-cho, Inage-ku, Chiba 263 Japan
Basic Engineering Co.Japan
16-11, Sakae-cho, Takasaki 370 Japan

Abstract
The objective of this study is to estimate accuracy of geometrically corrected GAC data. The used geometric correction method requires just a small number of GCPs using : ephemeris data. This method is based on photogrammetric theory. 20-30 GCPs and check ; points were collected from the Digital Chart of the World(DCW) for one GAC scene which , goes around the earth with the width of about 3,000 Km.

1 Introduction
Images acquired by remote sensing have different distortion due to the earth's curvature and rotation, satellite parameters( for example, speed, attitude and altitude ), scan skew and : projection of spherical surface on a flat image. These distortions prevent meaningful r comparison among multi temporal satellite images. Therefore geometric correction includes identifying the geographic coordinates corresponding to an image pixel( Direct image referencing) and locating a pixel corresponding to given geographic coordinates( Inverse image referencing ), is essential in many remote sensing studies-

NOAA AVHRR data are widely used in weather, climate and environmental studies. A VHRR data, particularly GAC data( Global Area Coverage) data are adaptable for global environmental study. However its ephemeris data is not exact and geometric distortions ..must be removed using some GCPs. The object of this study is to correct geometric distortions using photogrammetric theory and to estimate accuracy of the geometrically corrected GAC data- Geometric correction method using photogrammetry theory

If geometric correction of NOAA A VHRR is done only by using ephemeris data from ; National Oceanic and Atmospheric Administration, the corrected image has not enough r accuracy due to ephemeris error, time error between the satellite and receiving station and t satellite attitude error. Therefore it is necessary to use GCPs. The geometric correction V method applied in this study is developed by Hashimoto and Murail) in which position andattitude of the satellite are corrected using collinearity equation of photogrammetry .

2.1 Collinearity equation
To correct the A VHRR data accurately, it is necessary to calculate the position( X_o.Y_o.Z_o) and the attitude( w, F, k: roll, yaw, pitch) of the satellite exactly. Therefore we regardtheir parameters as exterior orientation parameters in photogrammetry and calculate themfrom collinearity equation. The satellite position is expressed by distance from the geocentric place(R), angle from equator plane(u), inclination angle(i), right ascension of ascending node(W). The target earth surface is expressed by geocentric coordinate system. The Image coordinates defined the right-handed coordinate system that directionto the is satellite trace direction and direction to the z is normal direction of satellite trace. Collinearity equation here means that center of the projection( position of the sensor) andthe image point and the target earth surface is in a line.

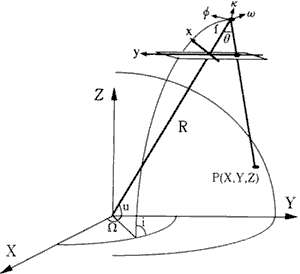
Fig.1 Collinearity equation
2.2 Parameters
Parameters( R , u , i and W ) are expressed by ephemeris data. Ephemeris data are sent by NOAA everyday. Ephemeris data are
a: Semi-major axis e : Eccentricity of orbit i: Inclination angle
l : Right ascension of ascending node w : Argument of perigee
M : Traverse angle of satellite position
If we consider that the motion of satellite is Keplarian motion, it obeys the Keplar's law.
M = E -e cos E ( E is angle of passage of perigee )
Then the satellite position( R, v) in the orbital plain is calculated from equations bellow
R=a( l-ecosE)

The parameters u is derived as u = w + v. Right ascension of ascending node(l ) is measured from vernal equinox. The right ascension of ascending node( l) in geocentric coordinate system is derived as

W = l + l_G
l_G : vernal equinox longitude
If ephemeris data are enough accurate, R, u , i and W can be calculated accurately by the above equations and unknown parameters are only the satellite attitude( w, f, k ). Since ephemeris data are not exact, we regard R , u , i and W as unknown parameters too.

3 GAC data
The used data is NOAA A VRRR Global Area Coverage( GAC ) Level 1 b data of July 30, 1992. This data was apart ARGASS(A VHRR GAC data set for Atmosphere and Surface Studies) which was originally produced by Dr. Compton J. Tucker of NASA Goddard Space Right Center .

4 Collection of GCPs
GCPs are collected from DCW( Digital Chart of the world ). The DCW is a comprehensive 1: 1,000,000 scale vector base map of the world. It consists of geographic, attribute and textual data that can be accessed, queried, displayed and modified with ARC/INFO software. . GAC image data were compared with DCW image to collect GCPs.

Fig.2 The DCW image nearby Japan S Geometric accuracy
Geometric accuracy
Geometric accuracy of the corrected image is estimated by check points. The check points are a part of GCPs which are not used for correction. The advantage of GAC image is that most image include seashore lines because the image scans around the earth. The result of accuracy will be reported at the conference.

Acknowledgment
Authors would like to thank Dr. Yoshiaki Ronda for providing GAC data in ARGASS. Reference

Reference

Toshiaki Rashimoto and Shunji Murai, Geometric Correction of NOAA A VHRR Imagerywith Few GCPs, SEISAN KENKYU, Vol. 43, No.8, pp.44-47, 1991.
W. j. Emery , J. Brown, Z. P. Nowak, A VHRR Image Navigation: Summary and Review, Photogrammetric Engineering and Remote Sensing, Vol. 55, No.8, pp. 1175-1183, 1989

Fig. 3 GAC image (July 30 1992)