GISdevelopment.net ---> AARS ---> ACRS 1995 ---> Digital image Processing A Technique for 3D Modelling of Buildings Taejung Kim and Soon Dal Choi Satellite Technology Research Center Korea Advanced Institute of Science and Technology 373-1, KuSung-Dong, YuSung-Gu, Taejun Korea Phone: +82-42-869-8629, Fax: +82-42-861-0064 E-mail: tjkim@satrec.kaist.ac.kr Abstract A fully automated technique has been developed for 3D mapping of buildings from high resolution aerial and space imagery ..This paper will briefly describe the basic principles of the technique and present the results .." from various images- The technique consists of three parts: building height extraction, building detection, and 3D modelling.. For building height extraction, a pyramidal matching algorithm has been developed.. This algorithm emphasises .the control between levels in order to reduce the blunder propagation.. For building detection, anew graph- r,. based algorithm has been developed.. This algorithm extracts lines from single image and store them and their ~ relationships in a graph. Building hypotheses can be generated by finding closed loops in the graph." 3D modelling of buildings can be achieved by combining the results from building height extraction and ..building detection. Buildings are modelled as planar or apex surfaces and heights from pyramidal matching are assigned to these surfaces.. Building detection output is used as interpolation boundaries.. The results from various images show that the developed technique can model buildings successfully. I. Introduction The extraction of man-made objects from remotely-sensed imagery is one of the fundamental tasks in remote ~ sensing as well as in image understanding. In particular, man-made objects such as roads or buildings are important features in urban areas and techniques to extract them have numerous applications in urban icc", mapping, urban planning and Geo-Information engineering.There have been several app~oaches prposed for automated building extration.. The most pular ones are perceptual groupIng [I] and lIne analysIs [2,3].. The use of shadow InformatIon and perspectIve geometry has .' also been used by manyauthors [4,5].. However, the nature of buildings in real world necessitate the need to ; include 3D analysis in building extraction: building detection performed in 2D cannot fully "understand"buildings in the scene.. For such purpose, stereo matching has been used with the combination of other approaches mentioned before. However, building extraction (in 3D) remains still difficult as it requires not only good low-Ievel vision techniques such as edge or line extraction but also good middle-level or high-Ievel vision techniques such as cognition and interpretation.. This paper describes a new approach developed for automated 3D building extraction.. The new approach uses a stereo matching technique to retrieve 3D information on buildings and a buitding detection technique to "recognize" buildings in 2D.. These two techniques are combined for 3D buitding e>.iraction.. The next section will describe briefly the principles of this approach.. In section 3. some results or building extraction will be presented.. Conclusions and future work will be discussed in section 4.. 2. A new technique The new technique can be divided by three parts: height extraction using a pyramidal matching algorithm, building detection using a line-relation graph and 3D modelling of buildings using the results from height extraction and building detection. This section will describe each of them briefly. Interested readers should refer [3,6,7,8] for more detailed explanation. 2.1 Height extraction For height extraction, a pyramidal matching technique was proposed and proved effective. Due to the nature ofbuildings, there are many abrupt discontinuities in any scene containing buildings. This violates theassumption of contiguous disparity field, which almost all stereo matching algorithms adopt. Previousexperiments with a adaptive least squares correlation matching algorithm showed that buildings in a scenemake blunders and isolated regions for stereo matching [6].pyramidal matching can partly solve these problems: it can reduce the magnitude of height discontinuities and hence) the number of isolated regions by averaging down the image resolution; it can also enhance stereo matching by utili sing the matching results of lower resolution as the initial guess for higher resolution matching; it can also enable a fully automated system by using automatically generated initial guess at the lowest resolution matching. One of the difficulties for any pyramidal matching approaches is the problem of "blunder propagation" : errors at the lowest resolution are amplified through image pyramid. In order to minimize this problem, a tile-based control strategy was developed. Tiles with a given size are defined across the image plane and only the best matched point within a tile is selected as the initial guess for the next resolution matching. This pyramidal matching algorithm was tested with many aerial and space come images and it produced successful results [9,10]. The results of experiments were reported elsewhere. 2.2 Building detection For building detection, a graph-based algorithm was developed [3]. This algorithm generates building hypotheses by line analysis and then verifies them using shadow information and/or perspective geometry. This algorithm needs only a single image and building detection is performed in two dimension. Firstly, lines are extracted in an image using several steps: edge elements are detected by a Canny-Petrou- Kittler filter; a connected edge labelling algorithm is applied; two end-points of a linear elements are searched for With end-point templates. A line is defined with two end-points. Small lines broken from a long line and parallel lines with a narrow gap are merged. . Secondly, the relations between lines are searched for. The line relations are classified as positive, negative, or parallel connection. The value of connection is also defined accordingly. Lines and line relations (type and value of connections) are stored in s graph. The nodes of the graph consist of lines and the arcs the relationship between lines. Thirdly, the system generates building hypotheses by finding closed loops in the line-relation graph. To traverse a graph, a depth-first search algorithm is used. In order to make sensible building hypotheses, the search is limited by some connection rules and the maximum number of nodes it visits. However, experiments with this method revealed some limitations, the main one being unable to generate any building hypothesis where lines from one or more sides of a building are missing. To overcome this limitation, the concept of "super" building hypothesis, the building hypothesis generated from a "U"-shaped chain, is introduced. Finally, building hypotheses are verified. Similar building hypotheses are merged and some small building hypotheses are removed. Similarity is defined when building hypotheses have all identical components but one in their search chains. Shadow analysis is performed and lines in a scene are classified into ground-level and building-level lines. False building hypotheses, which contains any ground-level line, are removed. For an oblique viewing geometry, vertical lines can be visible in a scene and perspective geometry can be used to verify building hypotheses. After detecting vertical lines, lines are also classified into building-level, middle- evel, and ground-level lines. Building hypotheses which consist of alone building-level lines are verified. After the verification procedure, a building hypothesis represents a whole or part of a building. 2.3. 3D modelling of buildings One of the weakest application areas of any mono scopic approach is the extraction of height or depth information. The building detection system described above suffers from the same drawback. Although some .indication of building height may be possible by shadow analysis and perspective geometry , the system cannot provide accurate information on building height. Stereo matching results usually give accurate height information. However, height is assigned only on grid-points and it is difficult to obtain the height of objects such as building roofs without further processing. Also ...there is a problem of height for urban areas. In such areas, the surface does not vary in a geo-statistical manner. Large areas of the surface are very flat or linearly varying and there are many cliffs due to building ..boundaries. Hence "kriging", one of the common techniques for height interpolation, cannot be applied. Height- interpolation requires external guidance or, alternatively, a proper statistical model of the surface should be modelled. The fusion of stereoscopic and monoscopic cues can potentially solve these problems [8] .Rich height information from the stereoscopic process can be used to assign height onto buildings. Building hypotheses t, detected by the monoscopic process can provide the external guidance of height interpolation so that interpolation only takes place within the boundary of a building hypothesis. From the pyramidal matching technique described in section 2.1, a matching list can be generated. From the building detection system described in section 2.2, building hypotheses are generated. Each building hypothesis provides interpolation boundaries and matched points in a matching list provide height " information. Using the matched points which fall in a building hypothesis, coefficients of a surface model of a building hypothesis are calculated. Interpolation is then performed using the surface model equation.11Three surface models were considered for building roofs: a planar, an apex, and a quadratic surface model. The.coefficients of each model can be calculated using the matched points within a building hypothesis through "least squares estimation. The estimation errors of three models are then compared and the model with the least : error is chosen as a proper surface model. However, previous experiments have shown that a quadratic surface .model has an unacceptable error when the number of modelling points is too small and these points are not ..well-distributed in a building hypothesis. Although there may be dome structures in a scene, these are rare and , could be dealt with by specialised processes. The quadratic surface model was, therefore, discarded. The surface is assumed to be either planar or apex. Also, if the estimation error of a surface model is larger than .some threshold value, the surface model is not accepted and a building hypothesis remains un-modelled. Afterchoosing a proper surface model, interpolation can be done simply by calculating the corresponding height using the surface model equation. 3. Results and Discussions Figure I(a) and (b) show an ISPRS test stereo pair ("Flat" area) supplied by the University of Sttutgart. The v" solution of images used for experiments was 24 cm. The height extraction system was applied to this stereo pair. A S-level image pyramid was generated by reducing the images successively by the factor of 2. pyramidal matching was applied to this pyramid and 3146 points were matched (83.6% of to matchable points).These points were convert Into ground coordinates by applying camera model and a Digital Elevation Model DEM) was generated. This DEM IS shown In figure I(c). this DEM had a RMS height error of I.I m compared to a ground-truth DEM. Height information was retrieved successfully using pyramidal matching. However, there are many "holes" in the DEM, in particular on the roofs of buildings. This indicates that the ..height discontinuities due to buildings still remain as an obstacle for height extraction. This is the currentlimitation of the height extraction system. Figure 1. (a) and (b) : An ISPRS test stereo pair. (c) A DEM from the hight extraction system. (d) A building detection output (c) A perspective view of buildings. Building detection was performed to the image in figure I(a). After line extraction. 844 lines were obtained From these lines, 996 line relations were found. A line-relation graph was constructed using the 844 lines as nodes and the 996 line relations as arcs. A depth-first graph traversal algorithm was applied to find closed is loops and "U"-shaped loops in the graph. 60 "normal" building hypotheses (closed loops) and 240 "super" building h)1><>theses ("U"-shaped loops) were found initially. After building hypothesis verification process, 28 "normal" and 22 "super" building hypotheses were finally obtained. Note that there has been a great reduction i r in the number of "super" building hypotheses after the verification process. This is because, in our implementation, every "normal" building hypothesis makes one or more "super" building hypotheses and these rc redundant "super" building hypotheses are removed after the verification process. Figure I(d) shows the 28 "normal" and the 22 "super" building hypotheses. There are 19 buildings in the scene. 10 buildings are fully and 9 buildings are partly detected. The 3D modelling of buildings was applied by fusing the pyramidal matching output and the buildingdetection output. From the 50 ("normal" and "super") building hypotheses, 23 building hypotheses were , modelled as planar surfaces and 1 building hypothesis an apex surface. However, 26 building hypotheses were c not m.00elled due to insuffic~en~ modelling points or a large estimation error. Al through all Welding roofs are . apex In the scene, many bwldIng hypotheses were modelled as planar surface. this IS vahd because many .if building hypotheses cover only half of building roofs which are planar. Height interpolation was carried out. using these surface models. Fire l(e) shows a perspective view of buildings after the height interpolation. A ~"c constant value of loom was assIgned to the 26 un-modelled building hypotheses to distinguish them from the ground plane. The perspective view shows that 3D modelling was performed successively. Many buildings have apex-shaped roofs. Some low buildings are due to the un-modelled building hypotheses with the constant height of l00 m. Figure 2(a) and (b) show another test stereo pair supplied by Ern Zurich. The resolution of the images was 15 cm. A 5-level image pyramid was created and the height extraction system was applied to this pyramid as before. 18448 matched points (91% of the total matchable points) were matched. After converting them in ..c ground coordinates, a DEM was generated (figure 2(c". In the DEM, height information even on the roofs of ~ buildings was successfully. 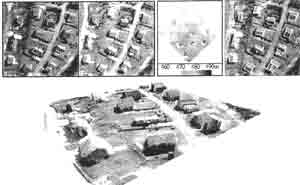Figure 2.(a)and (b) : Another test stereo pair. (c) A DEM. (d) A building detection output. (e) A perspective view of buildings. The building detection system was applied to the image in figure 2(b). After line extraction, 338 lines were ,.obtained. 508 relations between these lines were found and a line-relation graph was contracted accordingly.From this graph, 50 closed loops ("normal" building hypotheses) and 210 "U"-shaped loops ("super" building ..hypotheses) were initially generated. After the verification process, 27 "normal" and 8 "super" building ~ hypotheses was finally verified. These are shown in figure 2(d). There are 12 buildings in the scene. Among : them, 8 buildings were detected fully and 3 partly. However, one building in the middle of the scene was , completely undetected. There are three building hypotheses which are not from real buildings but from other ,.. objects (two of these do "look" like real buildings). The 3D modelling was performed as before. The 35 building hypotheses and the height information in the DE< were combined for height interpolation. 24 building hypotheses were modelled as planar surfaces and 5building hypotheses apex surfaces. 6 building hypotheses were not modelled. Height interpolation was carried out using these surface models. For the 6 un-modelled building hypotheses, a constant height value of 470mpc was assigned. Using these results, a perspective view of buildings was created (see figure 2(e". As shown in: the figure, 3D modelling was performed successfully. Many building roofs have apex-shapes. The flat buildingin the middle of the scene is due to the one undetected building. 4. Conclusions and future work In this paper, a new technique developed for automated 3D modelling of buildings was briefly described. The4 results shown support the good performance of the technique. This section will discuss some other aspects of the technique. There are many pyramidal matching algorithms developed and proposed so far. The major difference between the one described here and others is that the problem of blunder propagation was carefully considered. A naivepyramidal matching algorithm without considering this problem may fail to work in a extreme circumstances where, for example, there are a lot of height discontinuities in a scene.The building detection system described here also uses the concept of perceptual grouping but emphasises the connection between lines. The use of type and value of connections between lines is a very unique approach. ---One of the main differences between this building detection system and others is that this system works reasonably well without any verification process (results without verification process, however, were not presented in this paper due to the limited space). Compared to other systems, the number of building potheses removed after the verification process in small. The reason is because building hypotheses aregenerated very carefully in this system. (Other systems may apply "strong" verification process for successful building detection. ) 3D modelling of buildings was achieved by combining the height extraction system and building detectionsystem. In is worth noting that this 3.D modelling was done without any man intervention. This approachcan be a good example of the potential benefits due to the fusion of monoscopIc and stereoscopic processes. The major contribution of the work described in this paper is the development of techniques which can be used ~ for automated urban mapping. There are several aspects to be considered for the future work on this technique. As the 3D modelling is achieved only after quite a number of processes, there are many parameters to be specified by operators. Although most of them can be substitute automatically, some should be carefully chosen. This can be an obstacle for a "truly" automated system. In the building detection system, the verification process may need further development. Compared to other systems, the verification process used here is one of the simplest. This is partly due to the reliability of candidate building hypotheses as mentioned earlier. However, for a more robust system, further development on the verification processes should bring some benefits. References R. Mohan and R. Nevatia, "Using Perceptual Organization to Extract 3D Structures", IEEE Trans. on Pattern Analysis and Machine Intelligence, 14(6):616-635, June 1992 J. Shufelt and D.M. McKeown, "Fusion of Monocular Cues to Detect man-made Structures in Aerial Imagery", Computer Vision, Graphics and Image Processing: Image Understanding, 57(3):307-330, 1993 T. Kim and J-P. Muller, "A New Algorithm for Building Detection: A Graph-based Approach", IEEE Trans. on Pattern Analysis and Machine Intelligence, submitted, 1994 A. Huertas and R. Nevatia, "Detecting Building in Aerial Images", Computer Vision, Graphics, and Image Processing, 41:131-152,1988 M. Herman and T. Kanade, "The 3D Mosaic Scene Understanding System", From Pixels to Predicates edited by A.P. Pentland, pp. 322-358, 1986 T. Kim and J-P. Muller, "Automated Urban Area Building Extraction from High Resolution Stereo .Imagery", Image and Vision Computing, 1995, (in press) T. Kim and J-P. Muller, "Building Extraction and Verification from Spaceborne and Aerial Imagery using Image Understanding Fusion Technique", Proc. Ascona Workshop 95 on Automatic Extraction of Man- made Objects from Aerial and Space Images, Ascona, Switzerland, 24-29 April 1995 T. Kim and J-P. Muller, "Fusion of Stereoscopic and Monoscopic Cues for Urban Area Image Understanding", Computer Vision and Image Understanding, submitted, 1995 T. Kim and J-P. Muller, "Automated Building Height Estimation and Object Extraction from Multi- Resolution Imagery", Proc. of SPIE conference on "Integrating Photogrammetric Techniques with Scene Analysis and Machine Vi.sion II", SPIE Vol. 2486, Orlando, Florida, USA, 19-21 April 1995 T. Kim and J-P. Muller, "Effects of Image Resolution on an Automated Building Extraction System", Proc. of the 21 th Annual Co'!lerence of the Remote Sensing .S'ociety on Remote ,Sensing in ..4ction (RSS'95), ,S'outhampton, UK, 11-14 September 1995