A Massively Parallel Implementation of an Image Classifier

A Massively Parallel Implementation of an Image Classifier

¹P.A. Caccetta, ²N.A. Campbell and ¹G.A. West
¹School of Computing, Curtin University of Technology
E-mail : peterc@cs.Curtin.edu.au, geoff@cs.Curtin.edu.au
²CSIRO Division of Mathematics and Statistics
E-mail : normc@per.dms.csiro.au

Abstract
This paper describes the parallel implementation of a classifier based on maximum likelihood classification with pixel neighborhood modifications. This is used for remotely sensed data which are large in comparison to other forms of 2D spatial data. The computational complexity of the algorithm restricts its use and has lead to an implementation on a SIMD processor namely the DEC mpp. Issues addressed in the paper include: the ease of porting of the serial algorithm to a parallel machine and the resulting improvement in throughput due to the increased speed of computation.

1. Introduction
Maximum likelihood classification (MLC)has a long history as a tool for the interpretation of remotely sensed data. The technique is used in isolation [12] or in conjunction with other methods [9]. The algorithm is computationally expensive which is exacerbated by the large datasets that are typical of remote sensing e.g. 2048X2048 pixels in size with 6 bands of 8-bit data. For this reason implementing this form of classifier on a massively parallel machine is desirable. The important issues are the ease with which it can be done and the increase in computational performance over typically available serial machines.

The MLC technique takes the raw data and transforms them into an image composed of labels defined by the user. Labels are often called Classes and the resulting image a classified image. In essence, MLC involves allocating a pixel to a class for which it shows greatest affinity. Classes are modeled by multivariate distributions whose parameters are estimated from representative samples of the class. The multivariate distributions are then used to assesss which class an individual pixel is most likely to belong.

This paper considers the problem of processing the remotely sensed data once the class models have been obtained (that is the classifier has already been (rained). In the following processing based on multivariant distributions will be referred to as spectral processing.

Spectral processing tends to produce images that have a certain amount of noise. In the current context, noise is when a pixel's data vector has affinity for a class other than its true class i.e. an error in classification. Noise can be the result of a pixel sample containing more than one cover class, in which case the pixel is referred to as a mired pixel, or the result of errors of omission and commission present in the classification process A typical result of noise is that a pixel is classified as belonging to a class not in agreement with its general surroundings e.g. a single pixel of lupins in a paddock of wheat. Neighborhood techniques are incorporated into the classification procedure to reduce the effects of noise by taking account of neighboring pixel classifications to aid the classification of the current pixel. Processing based upon neighboring information will be referred to as spatial processing. The overall algorithm iteratively performs spectral and spatial processing to produce a classified image, and for large images becomes computationally expensive.

This paper outlines issues that were addressed during the porting an existing serial based version of the algorithm to a DECmpp massively parallel processor, and discusses the computational advantages in doing so. the original serial code was written in FORTRAN 77 and based on a SUN platform. The target machine was a DECmpp 12000 comprising 2048 comprising 2048 processors. Paralleled code was created using DEC MPFORTRAN version 2.1.46 as opposed to the more efficient parallel C language (MPL) because the code was already in FORTRAN.

The remainder of this paper is divided as follows. Sectin2 describes the architecture of the processor which governs the porting process. The classification algorithm is described in Section 3. Section 4 describes how parallelism is exploited in the algorithm. Section 5 discusses issues that arose with respect to the port to the DECmpp. Finally Section 6 discusses the computational performance and improvement in the execution time.

2 The DECmpp Massively Parallel Processor
The DECmpp 12000 is a parallel processor based on a single instruction multiple data (SIMD) architecture [11]. It is a modern implementation of ideas originally developed on the CLIP series of machines [5,6], and the original MPP [1]. These were characterized by having many simple processors with a small amount of local memory and 4 or 8 way connectivity with their neighboring processors. They are highly suited to operations that operate on single data elements or small neighborhoods e.g. 3x3. These operations are very common in image processing and analysis algorithms such as distance transforms [4] and skeletonisation [8]. It consists of a front end workstation (FE) and a backend parallel processing unit called the |Data Parallel Unit (DPU). The DPU has two components the processor array consisting of many Processing Elements (PEs) and the Array control Unit (ACU) which controls the PE array and performs operations on singular data.

Each PE in the array consists of a simple 4-bit ALU, a floating point co-processor and memory that is local to the PE. The PEs are arranged in a grid which incorporates specialized hardware for inter-PE communications. The hardware allows efficient communications between a PE and its immediate 8-connected neighboring PEs, that is if a PE is located at positions (i.j) on the grid, then efficient communications exists with the PEs located at (i-1,), (i+1,j), (i-1,j-1), (i-1,j+1), (i,j+1), (i,j-1), (i+1,j+1), and (i+1,j-1), This form of communication is implemented in hardware and is referred to as the X-net. The connectivity is arranged as a toroid in which the top row, and the left column of the array is connected to the right column. This allows sufficient raster shift communication to be used.

Two programming languages exist for the DECmpp. (1) MPFORTRAN which is based on FORTRAN 77 with extensions from VAX FORTRAN and the FORTRAN 90 ANSI standard, and (2) MPL which is based on ANSI C, and like MPFORTRAN has parallel constructs for handling arrays and I/O code written in MPL as MPFORTRAN 2.1.46 did not support reads on byte data and the rest written in MPFORTRAN.

MPFORTRAN provides high level constructs for handling array operations, where ideally each PE performs the processing for one element of the array. When an array has dimensions larger than the dimensions of the PE grid, then the array is mapped to the grid such that a PE may process more than one element. The process of mapping an aray which is larger that the PE array is Called virtualization. Performing virtualization efficiently for arrays of different sizes is a complex problem. for MPL virtualization has be addressed by the programmer whereas MPFORTRAN automatically handles virtualization.

The DECcpp used was configured with 2048 PEs arranged on a 32X64 grid. Each PE had 64k of local RAM nad the DPU hardware is scalable to 64k PEs.

3 The Classification Algorithm
This section provides an overview of the classification algorithm, and is based on previous work (10,3,2,). In the following. it is assumed that an input image is available and the class means and covariance matrices for each class have been estimated during training.

3.1 Spectral Processing and Typicality Probabilities
Assuming multivariate Guassian densitis for k classes and an image composed of m spectral bands, this corresponds to calculating, for each class k, the density function

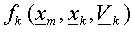defined as: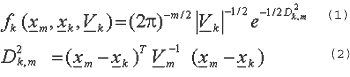

where x_k is the vector of sample means, V_k is the sample covariance matrix, x_m is the pixel data vector and D²_{k, m} is the squared Mahalanobis distance for vector x_m and class k.

The density Function

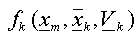is also used to calculate typicality probabilities. These probabilities consider each class in isolation, and are used to judge whether a pixel conforms to the class statistics. If it does not, it is labeled as being atypical. for more details see [3]:

3.2 Spatial Processing
Neighboring pixel class labels produced from the previous stage are used to influence the local influence the local prior probability of the pixel in the current iteration. For a pixel located at image position (i.j), the neighborhoods considered are

N ₁ = {(i-1, j), (i+1, j), (i, j-1), i, j + 1)} (3)
and
N₂ = N₁ U {(i-1, j-1), (i+1, j-1), (i-1, j+1), (i+1, j+1)} (4)
where N₁ is referred to as a first-order neighborhood and N₂ a second-order neighborhood. The distinction is necessary because the distance between first-order neighbors is 1.0 and the remaining neighbors is , This difference is taken into account in the algorithm.

A count n_k of neighbor class labels is made (that is, there are nk neighbors having class label Ck) and the probability of the pixel belonging to class k given neighborhood N is calculated by:

P(C_k|L_N) = A^-1e^0.5(ak+bknk) (5)
where L_n denotes the labelling of pixels in N, a_k and b_k are user controlled parameters, and A is a normalising constant.

Hence the probability of a class label is increased as a function of n_k. If n_k is large then the probability will increase and visa versa for a low value of nk The constant is used to keep the sum of the probabilities for all classes equal to 1 . the parameters a_k and b_k are used to tune the system.

3.3 Posteriour Probabilities
Results from sections 3.1 and 3.2 are combined to form the posterior probabilities of class membership. The values are calculated as:

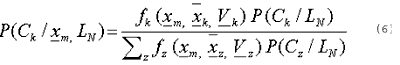
If super-classes ae specified (a class that is made up of two of more classes), then the posterior probabilities for a pixel belonging to each super-class is evaluated by simply adding the probabilities for all its member classes.

4 Algorithm Pseudo Code and Complexity
The pseudo code for the critical section of the serial code implementation is shown below. The loop I controls the number of iterations, L is the number of image lines, P is the number of image pixels per line. N is the numbers of image bands and C is the number of classes. The functionality of the pseudo code functions correspond to the appropriate descriptions given in section 3.1.

The complexity of the calculation is O[LPCN2] Of the functions in the critical loop. SPECTRAL_PROCESSING () has the highest order, being proportional to N2

5 Exploiting Parallelism-Mapping Data to Processors
From the algorithm complexity equation it is observed that a number of variables affect the computation time. Typically, the total number of pixels LP in the image is the dominating factor, being several orders of magnitude greater than that of the number of PEs. All other variables have dimension less than that of the number of processors available, hence parallelism in pixel processing was used.

The volume of data typically processed precludes loading the entire image into the DPU and hence sections of the image must be processed separately. Further, band-interleaved by line (BIL) data format was specified for input and output files making lines of image data a convenient partition. As the dimension of an image line are of the same order as that of the number of PEs i.e. 2048, it was convienient spread the pixels of the line across the PE grid, with one pixel (and corresponding calculation) per PE. the pixel iteration loop in the serial code thus became redundant.

Spectral processing does not impose any constraints on the relative orientation of pixels on the PE grid and as such data could be mapped to the grid in any fashion. The determining factors for choosing an image line to PE grid mapping was the requirements of spatial processing and efficient I/O routines. Considering only spatial processing, it would seem natural to locate a pixel at grid position (i,j) with neighbors at locations as defined for N2 or N2 and make use of the X-net operations that explicitly represent these directions.

The I/O mapping from BIL format to this scheme would be complicated and, as a consequence, suffer inefficiencies such as unnecessary file seeks, Further, I/O is potentially more time consuming than spatial processing so it was given greater importance.

Pixels are mapped in a raster scan fashion across the PE grid, such that the grid can be considered a one-dimensional array of processors. This is similar to the scheme adopted for CLIP4S [7] in which a small rectangular array was rejected and replaced by an array 512X4 which scans down an image row by row. When the image row is larger than the number of processors, virtualisation occurs. The virtualisation used is the MPFORTRAN one-dimensional array default-cut and stack. That is, if N is the number of processors and m is a non-negative integer, pixel mN+i maps to PE i. All data dealing with an image pixel were mapped in this way.

A simple scheme using three rotating buffers was used for spatial processing. Each buffer contains one line of class labels produced from the previous iteration. Given this scheme, a Pe stores locally its own label and the labels of its north and south neighbors. Labels of other neighbors are assessed by communicating with the left and right PE, which corresponds to a PE grid raster shift operation which is efficiently handled by X-net communications.

Table 1 Classification times for the processing stages

	Iteration 1	Iteration 2	Iteration 3	Total time
Serial Time T1 (sec)	5099	6010	15255	26364
Parallel Time T2 (sec)	325	360	594	1279
Ratio T1/T2	16	17	26	21

6. Computational Performance
A test area of Landsat TM data was processed on the DECpp and on a SUN SPARC II workstation and the computation times recorded in table 1. The dataset consisted of 2170 lines with 2048 pixels per line and 6 bands per pixel. Spectral signatures for 106 classes were used which were grouped into 5 super-classes.

From the tables a number of observations can be made.

On average the parallel implementation was 21 times faster than the serial version.
The first iteration is the least time consuming as the only calculation performed is SPECTRAL_PROCESSING(). In fact, in all but the last iteration only the exponent of equation 2 is calculated.
Comparing iterations 1 and 2, SPATIAL_PROCESSING () is not that expensive in terms of computation time, and comparing this difference with the total time for iteration 3, the computation time for SPATIAL_PROCESSING is insignificant.
The final iteration is the most expensive accounting for almost half (46%) of the entire computation time.

Time profiling of the parallel code revealed computation time was : (45%) front end (FE), 50% DPU and 5% FE-DPU communication. Function profiles revealed that SPECTRAL-PROCESSING() accounted for 50%, TYPICALITY () 10% and SPATIAL-PROCESSING ()3%, I/O was insignificant and the remaining 37% was spent by the FE servicing the DPU. Function profiles suggested that of the 45% total time consumed by the FE, most of it (37/45) was actually used to set up communications in some form or other with the back end (BE), which, once set up. FE to BE communication accounted for 5% of the total time.

The time spent by the FE servicing the DPU is an artifact of the MPFORTRAN compiler, which places scalar operations on the FE which then have to be communicated to the DPU (this includes indexes to arrays). This extra time could be eliminated by an MPL version of the code which can perform scalar operations on the ACU, thus avoiding costly FE to DPU communications. However this would incur much more code development time.

7 Conclusions
This paper has described the porting of a heavily used classification algorithm to a SIMD machine to enable higher throughput. The DEC MPFORTRAN compiler provided a convenient means for creating a massively parallel version of the existing FORTRAN 77 coded algorithm. Because of the implicit nature of the MPFORTRAN parallel constructs, the DEC MPPE debugging environment provided an invaluable tool for code development a sit allowed easy tracing of DPU arrays and array mappings.

The algorithm was well suited to a SIMD architecture as it used pixel-based as well as local pixel neighborhood operations. Hence considerable computational improvements would be expected over a serial implementation. Testing has shown a computational advantage of 21 times over that over that of a SUN SPARC II. As with all high-level languages, there are limitations revealed when implementing one particular algorithm. Analysis of the performance of the MPFORTRAN compiler reveals that the performance of the parallel code is front-end CPU bound This can be improved by implementation of the critical routines in C using The DEC MPL compiler.

8 Acknowledgements
This work was supported by a grant from the DEC External Research Programme which funded P.A. Caccetta and the DECmpp. Further funding and the data were supplied by the CSIRO Division of Mathematics and Statistics.

References

K.E. Batcher. Design of a massively parallel processor. IEEE Transactions on Computers. C-29 (9) : 836-840, September 1980.
J. E. Besag. On the statistical analysis of dirty pictures (with discussion), Journal Royal Statistical Society Series B, 48; 259-302, 1986.
N.A. Campbell some aspects of allocation and discrimination. Multivariate Statistical Methods in Physical Anthropology, Pages 177-192, 1984.
S. Campbell and G.A. W. West. Parallel implementation of salience distance transforms. In Proceedings of PART-95, Perth, Western Australia, 1995.
T. J. Fountain CLIP4: progress report. In M. J. B. Duff and S. Leviaidi, editors, Languages and Architectures for Image Processing, pages 283-291, Academic Press, London, 1981.
T. J. Fountain. The development of the CLIP7 image processing system. Pattern Recognition Letters, 1:331-339, 1983.
T. J. Fountain, M. Postranecky, and G.K. Shaw, The CLIPAS system, Pattern Recognition Letters, 5:71-79, 1987.
C.J. Hilditch. Linear skeletons from square cupboards. In Machine Intelligence IV. Edinburgh University Press, Edinburgh, 1969.
L.L.F Janssen and H. Middelkoop. Knowledge- based crop classification as a landsat thematic mapper image. International Journal of Remote Sensing, 13:2827-2837,1992.
H. T. Kiiveri and N.A. Campbell. Allocation of remotely sensed data using markov models for image data and pixel labels, Australian Journal of Statistics, 34(3):361 374, 1992.
J.B. Rosenberg and J. D. Betcher, Mapping massive SIMD parallelism onto vector architectures for simulation. Software-Practice and Erperience, 19(8):739 756, 1989.
J. F. Wallace and G. A. Wheaton, Spectral discrimination and mapping of land degredation in western australia's agricultural region. In 5th Australiasian Remote Sensing Conference, Perth Western Australia, pages 1066-1073, 1990.