| GISdevelopment.net ---> AARS ---> ACRS 1995 ---> Water/Marine Resources |
Estimation of Chlorophyll
Concentration in Lakes and Inland Seas From Near-infrared and Red Spectral
Signature
Kazuo Oki* and Yoshifumi
Yasuoka**
National Institute for Environmental Studies,
16-2 Onogawa, Tsukuba, Ibaraki, 305 Japan
K. Tokumura
*Institute of Socio-Economic Planning, University of Tsukuba
**National Institute for Environmental Studies
Contact : Y.Yasuoka National Institute for Environmenal Studies
16-2 Onogawa, Tsukuba, Ibaraki 305, Japan
Tel. +81-298-50-2543, Fax +81-298-51-4731,
E-mail yyasuoka@nies.go.jp
Abstract National Institute for Environmental Studies,
16-2 Onogawa, Tsukuba, Ibaraki, 305 Japan
K. Tokumura
*Institute of Socio-Economic Planning, University of Tsukuba
**National Institute for Environmental Studies
Contact : Y.Yasuoka National Institute for Environmenal Studies
16-2 Onogawa, Tsukuba, Ibaraki 305, Japan
Tel. +81-298-50-2543, Fax +81-298-51-4731,
E-mail yyasuoka@nies.go.jp
A remote sensing method to estimate distribution of rich chlorophyll concentration in takes or inland seas in proposed. First, the basic relationship the chlorophyll concentration and the spectral reflectance of water was investigated. As a result, chlorophyll estimation model was derived using the ratio of spectral reflectance at two different wavelengths of 675 nm (red range) and 700 nm (near-infrared range). It was found that the spectral signature of near infrared range is investigate the behaviour of the proposed model was used in rich chlorophyll water types. Furthermore, the amount of specular reflection from the water surface was assessed based on the spectral signature data measured above and below the water surface. The percentage of specular reflection was evaluated at least 20% of the total radiance at the surface within the range of 400nm. Finally a method to remove the effect of specular reflection at the water surface was investigated for the proposed model. The model for specular reflection was proposed to eliminate its effect and to improve chlorophyll estimation accuracy.
1. Introduction
Environmental degradation in lakes and inland seas has been very serious due to extensive land cultivation or urbanization around area. In particular. Eutrophication has caused massive growth the phytoplankton or zooplankton in water and gives serious physical, social and economic impacts to the area. Measuring chlorophyll contents in the plankton is of significant importance in tackling with the water pollution problem. It is, however, not easy to monitor water quality distribution over a large area periodically based on a conventional water sampling and analysis method. In this papper, a remote sensing method to estimate the distribution of chlorophyll concentration is proposed. Lake Kasumigaura is selected as a test site for the study, and spectral signatures of water, spectral reflectance below and above water surface was measured together with several water quality parameters including chlorophyll, suspended solids and transparency.
Several models has been proposed for the estimation of chlorophyll concentration of lakes and oceans however, most of them utilized only the spectral signatures in visible range (e.g., Gordon et al. 1983; Okami et al. 1982). It was because the water body usually absorbes the near-infrared spectral radiation and there is no reflectance from water in that range. In general, their models don't operate well to estimate rich chlorophyll concentration. In this study, chlorophyll estimation model which is effective in remote sensing of rich chlorophyll water area like lakes or inland seas was proposed.
The effect of specular reflection at the water surface was also one of important problem for estimating chlorophyll concentration by remote sensing. Takashima et al. (1986) developed model in order to remove effect of specular reflection at the water surface based on Cox and Munk model. However, the Takashima model has not been verified, if it would oerate well in rich chlorophyll water area like lakes or inland seas. In this study, the model was verified based on the spectral signature data measured above and below the water surface.
2. Chlorophyll-a Estimation Model
2.1 Radiative Transfer Model at the Water Surface
The spectral reflectance R of radiance of irradiance at the water surface is defined by
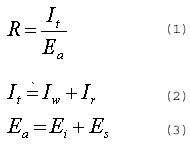
Where I, is the up welling spectral radiance from the water surface. E is the downward irradiance onto the water surface from total solar radiation. I is the upwelling spectral radiance just above water surface. I, is the upwelling spectral radiance reflected from water surface due to total solar radiance. E, and E, are the downward irradiance onto the water surface due to direct sun and the diffuse sky light, respectively. In this report, it is assumed that the water body is a lambertian reflector and the angular distribution of radiance in the lower hemisphere of the water surface is uniform for radiance traveling up ward. Then I, can be expressed as
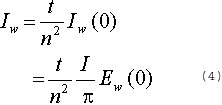
Where t and n are transmittance and refractive index from water to air, respectively. 1(0) is the upwelling spectral radiance just below the water surface. E, (0) is the upwelling spectral irradiance just below the water surface. We cannot, however, measure it directly, therefore, E. (0) was estimated from the upwelling iiradiance at the depth of Zas
Where k is the extinction conefficient for the upwelling irradiance of the water, expressed as
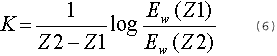
2.2 Measurement of Spectral Reflectance at Lake Kasumigaura
The upwelling radiance of the Lake Kasumigaura was measured by using spectroradiometer at the water surface and at several depth layers at the each points (Pt1 Pt18). The Pt 10, Pt11 to Pt 16, and Pt17 to Pt18 were measured on 10 September 1993, 22 April 1994 and 27 July 1994, respectively. The measurements covers the wavelength interval 400nm to 850nm with a resolution of 2nm. At the each points, were measured as follows.
- Upwelling spectral radiance from the water surface (I)
- Upwelling spectral irradiance of the underwater at depths of 10 and 40cm From the water surface (Ew, (0.1), Ew (0.4))
- Spectral irradiance of white board (Es)
2.3 Selection of Effective Spectral Reflectance to Estimate Chlorophyll-a concentration
We ignored reflection for making stable chlorophyll-a estimation model, and the Eq. (1) was given I w instead of It ,. Fig. 1 shows spectral reflectance examples calculated just above the water surface at Pt1, Pt6, and Pt18 of Lake Kasumigaura. It show that the richer the chlorophyll concentration is the stronger the absorption of radiance of 675 nm is.
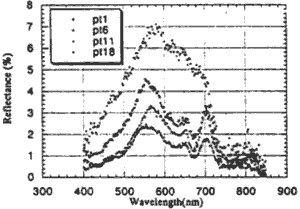
Figure 1: Spectral reflectance calculated just above the water surface at Lake Kasumigaura.
It was reported that the ratio of spectral reflectance at two different wavelengths was well correlated with chlorophyll concentration at Lake Kasumigaura polluted by many particles (Okami et al. 1982) however, it has not been confirmed numerically. In this study, regression analysis was used to evaluate the relationship between chlorophyll-a concentration and ratio of spectral reflectance at two different wavelengths in various conditions of Pt1 to Pt18.
Fig. 2 shows distribution of correlation coefficient in the three dimensional space with the denominator and numerator of ratio of spectral reflectance at two different wavelengths. It is found that the ratio of spectral reflectance of 675 nm and 700nm, R700/R675 was the best correlation of all patterns within the range of 400nm through 850nm. The correlation reflect light around 700nm. It was reported that up ward radiance at the wavelength of around 700nm was due to fluorescence of chlorophyll-a giving an effect on the reflectance peak and the peak is shifted toward longer wavelength as the chlorophyll-a concentration increase (Kishino et al. 1986). However, the effect of fluorescence was't clearly shown in Therefore, the effect of fluorescence is ignored in this study and we propose R700 / R67 model for estimating chlorophyll-a concentration. Fig.3 shows relationship between R100/R67 and chlorophyll-a concentration.
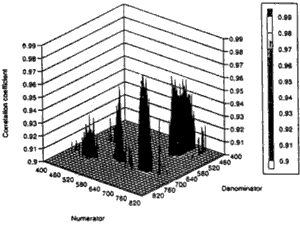
Figure 2: Distribution of correlation coefficient in the three dimensional space.
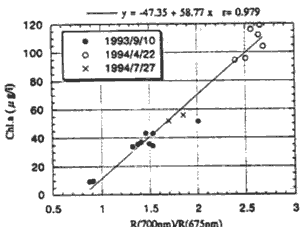
Figure 3: Relationship between Chl concentration and ratio of reflectance at two different wavelength
3. Verification of Chlorophyll-a Estimation Model
Ocean color spectra have been computed by means of the two-flow model by many investigators, however, the final mathematical expressions obtained by each of them differ to some degree. In this study, the following equation for irradiance reflectance given by Morel et al. (1977) is used.
| Rl = 0.33 | bl ------ al |
where al and bl are the absorption coefficient and backscattering coefficient of wavelength ? respectively. The a ? and b ? can be expressed as
al = awaterl + botherl + aChll (9)
where bwaterl , botherl and bChll are backscattering coefficient for pure water for chlorophyll-a and chlorophyll-a. bwaterl, botherl and bChll are absorption for pure water , suspended particles except for chlorophyll-a.
We assumed as follows;
Assumption 1: The water type polluted by many particles can be expressed as
Bwater<<b other Assumption 2: okami et al. (1997) assume that the dependence on wavelength of backscattering coefficient is constant. We also assumed as
from assumption 1 and 2 . the Eq .(8) can written as
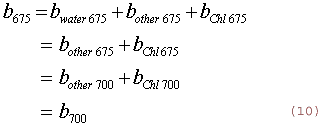
The absorption cofficient for chlorophyll-a of Eq .(9) is considered to be linearly releted to chlorophyll -a concentration C, that is
Where aChll is the absorptionn cofficeint per unit chlorophyll -a concentration . Using Eq. (7) through (11), the proposed chlorophyll estimation model can be expressed as
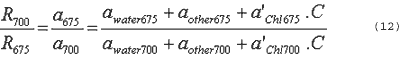
It is found that Eq. (12) can consequently ignore backsattering coefficent using ratio of spectral of 75 nm. and 700 nm.
In this study, the values of aother 675 and aother 700 by Okami et al. (1982) were used. The values of a ch1675 a ch/700 and a ch1650 reported by Morel et al. (1977) were used, and a water 675 and a water 700 were adopted from smith (1981)
Fig. 4 shows comparison between chlorophyll-a concentration and R700/R675 of value calculate from Eq. (12) and value measured. It is found that the calculated R700/R675 accord with the measured R700/R675 when chlorophyll-a concentration is less than 60 mh/l however, they don't accord with each other when chlorophyll-a concentration is greater than 90 One reason might be that the assumption 2 don't hold good. It is because the value of B ch 1675 decrease with the increase in chlorophyll-a concentration.
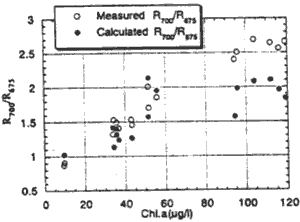
Figure 4: Comparison between measured R700/R675 and calculated 700/R675
Fig. 5 shows the result of R700/R675 simulated by using Eq. (12) in varing chlorophyll-a and suspended solids concentration. It is found that the R100/R675 depend on SS concentration when chlorophyll-a concentration is greater than 30 however the R700/R675 has nothing to do with as concentration when chlorophyll-a concentration is less than 30 mg/l. Therefore the R100/R675 can extract chlorophyll-a concentration which is less than. 30mh/l
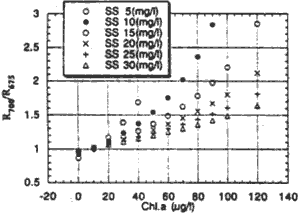
Figure 5: Simulation of 700/R675 with varing Chl.a and SS concentration.
4. method to Remove the Effect of Specular Reflection
Fig. 6 shows a part of ratio (Ir/It)( of upwelling spectral radiance (I, (=I,-1)) reflected from water surface due to total solar radiance to upwelling spectral radiance (I) measured at the water surface of Pt11. The effect of specular radiance within the range of 550nm through 700nm is the smallest within the range of 400nm through 850nm, however, the percentage is evaluated at least 20% of the total radiance at the water surface. Therefore, a method to remove the effect of specular reflection at the water surface must be investigated for the proposed chlorophyll-a estimation model.
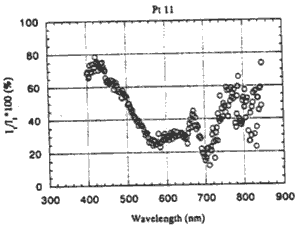
Figure 6: Relationship between t/t- and wavelength at point 11.
4.1 Specular Reflection Model
Takashima et al. (1986) developed the model removing effect of specular reflection at the water surface based on Cox and Munk model. In this model, it is a assumed that the wind-ruffled water surface consists of a collection of individual facts obeying an isotropical Gaussian distribution.
The I measured of spectroadiometer must be measured k times at the water surface for obeying an isotropical Gaussian distribution, i.e.,
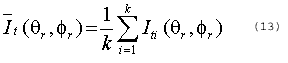
where is average of over k times measurements. The can be written as
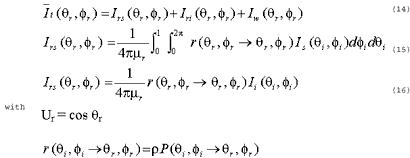
where( q and f) is radiance reflected from water surface due to diffuse sky light . I rs ( qr and fr) is radiance reflected from water surface due to diffuse sky light . . I rs ( qr and fr) is radiance reflected from water surface due to diffused sky light . Iri qr and fr is radiance reflected from water surface to direct sunlight Iw ( qr and fr) is radiance just above water surface. Is( qi and fi) and Ii ( qi and fi) are downward radiation onto the water surface to diffuse sky light and direct sunlight The factor r is the Fresnel reflectance of water. is the fraction of water surface with the required orientation to reflect light from ( qi and fI) to (qr and fr) and is the probability that an individual facet is visible. is given by
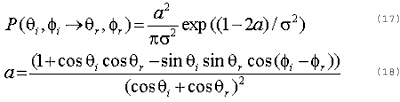
where s is related to the wind speed W[m/s] measured above the water surface as
Therefore, radiance Iw just above water surface from Eq. 14 can be written as
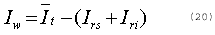
4.2 Verification of Specular Reflection Model
We used data of pt11 pt18 measured wind speed at the water surface. The radiance just above water surface calculated from Eq. (20) based on specular reflection model
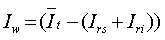
and the radiance just above water surface calculated from Eq. (4)
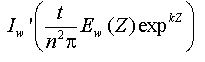
were compared . The wind speed was used average of Pt11 to Pt16 and Pt17 to Pt18, and they were 2.022[m/s] and 1.283 [m/s], respectively.
Fig.7 shows a part of spectral radiance distribution of It, Iw at the Pt11. Furthermore, fig. 8 shows relationship between Iw and Iw` of all data. It is found that the radiance just above water surface calculated form Eq. (20) and Eq. (4) accord with each other (Iw~Iw`), and the specular reflection model can remove the effect of specular reflection at the water surface.
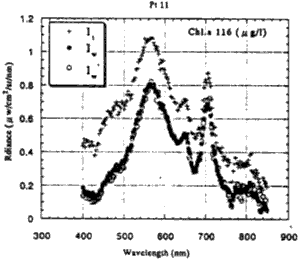
Figure 7: Spectral radiance of t, t, t, at Lake Kasumisaurqa Wind speed is 2.022(m/s).
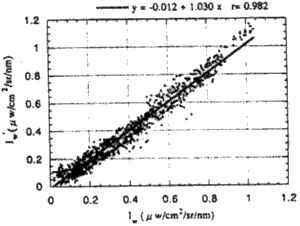
Figure 8: Relation between t and t'.
5. Conclusion
The followings have been shown in this study
- Chlorophyll estimation model was derived using the ratio of spectral reflectance at two different wavelengths of 675nm (red range) and 700nm(near-infrared range). The correlation coefficient was 0.979.
- It was found that the calculated R77/R675 from Eq. (12) accorded with each other when chlorophyll- a concentration is less than 60m g/l, however, they don't accord with each other when chlorophyll- a concentration is greater than 90m g/l.
- The value of R700/R675 by using Eq. (12) in varing chlorophyll-a and suspended solids concentration was simulated. It was found that the R77/R675 depend on SS concentration when chlorophyll a concentration is greater than 30mg/l. Therefore the R700/R675 can extract chlorophyll- a concentration which is less than 30m g/l.
- The percentage of specular reflection was evaluated at least 20% of the total radiance at the surface within the range of 400nm through 850nm.
- It was found that the radiance just above water surface calculated from Eq.(24) and Eq.(4) accord with each other (Iw~Iw`) and the specular reflection model can remove the effect of specular reflection at the water surface.
- Gordon, H.R. et al., "Phytoplankton Pigment concentration in the middle Atlantic Bight: Comparison of ship Determinations and CZCS Estimates ", APPLIED OPTICS Vol. No. 1 pp.20-36, 1983.
- Kishino, M., et al., "Theoretical analysis of the in situ fluorescence of chlorophyll a on the underwater spectral I rradiance ", La mer, vol.24, pp.130-138,1986.
- Morel, A.,et al "Analysis of variations in ocean color", Limnol. Oceanogr., Vo.22, pp. 709-722,1977.
- Okami, N., et.al, "studies on Ocean color spectrum (in Japanese)" , Bull. Coast. Oceanogr., Vol.15, No. 1 pp.56-66,1977
- Okami, N., et al., "correlation Studies between Spectral Radiance Reflection and water Quantities in Lake Kasumiga-ura",
- Journal of the Remote Sensing society of Japan, Vol.2no.1 pp 21-31,1982.
- Smith, R.C. et., al, "Optical properties of the clearest natural waters (200-800nm) " AFFLIED OPTICS, Vol. 20, NO. 2 ,pp.177-184,1981
- Takashima, T.,et.al, " A computational Procedure of the Upwelling Variation Emerging from the Atmosphere- Ocean System", Journal Of The Remote Sensing Society Of Japan, Vol.6 , No, 1 ,Pp 5-33,1986