New Texural Extraction Method Using Rolling Ball and Riping Membrane Transforms

New Texural Extraction Method Using Rolling Ball and Riping Membrane Transforms

Mazlan Hashim
Faculty of Geoinformation Science & Engineering
Universiti Teknologi Malaysia
Locked Bag 791, 80990 Johor Bahru, Malaysia
Tel . + (07)-5502969, Fax: + (07)-5566163
e-mail: mazlan@fksg.utm.my

Abstract
The inherent spatial information within a satellite remotely sensed data has shown a significant contribution to the classification of an image. In this, paper, two new textural approaches, namely the Rolling Ball Transform (RBT) and Ripping membrane (RM), were examined and analysed for image classification. the classification results are presented in the following models: (I) textural information alone, (ii) combination of best textural information and spectral data, and (iii) spectral data alone. Comparison of classification results obtained from the two new textural methods with three commonly textural extraction techniques : grey level co-occurrence, local statistical transform and convolution filtering masks were also carried out. Result of this study shows that the new textural extraction methods as one of the possible methods to increase the classification accuracies of the land use classes. The best results were obtained when textural information was combined with raw data. The new textural approaches- the RBT and RM both showed the most stable textures. RM textures from range 20 was the best overall textural extraction method.

1.Introduction
The use of spectral data alone in the classification has limited success due to the high variability within the spectral data. This variability is attributed to the within -class variances caused by the fragmented nature of the class e.g. urban contains varieties of urban structures like roads of various sizes and surface types, building variety and also variable vegetation cover. Even in the current high spatial resolution satellite data such as the Landsat TM, these small fragments and also other fragments found in most land use categorical classes as previously shown in Hashim (1995) are usually at subpixel resolution. Hence, classification of such classes spectral data alone is difficult.

The above-mentioned spectral variations are often referred to as inherent spatial information. Spatial information of remotely sensed data is assumed to be characterizes by the image texture (Haralick et. Al., 1973) which is an amalgam of geometrical properties (shape, size position, site, distribution) and the sensor imaging characteristics. Incorporating textural information into the image classification process may therefore provide a means of characterizing the classes within the land use classification system.

In this paper the incorporation of texture for improving image classification for land use mapping will be examined. Five textural extraction methods are employed : (1) grey level co-occurrence matrix (GLCM) (Haralick et. Al., 1973); (ii) Local statistical transform (LST) using median filter; (iii) convolution filtering masks (CFM) using Thomas et. Al. (1987), and Ford et. Al. (1983); (iv) rolling ball transformation (Sternberg, 1983; Stenberg, 1986); and (v) ripping membrane transformation (Blake and Zisserman, 1988). Emphasis, however, is place to the last two new textural extraction methods. These two methods were originally proposed as algorithms for use in biomedical image processing and visual reconstruction, respectively. In this study, the adapting of these methods will be examined by varying the parameters that best describe the textures of interest.

2.The Rolling Ball Transformation (RBT)
The RBT is mathematical morphological transformation first proposed as an algorithm to minimise image background noises. The RBT was proposed in this paper as a new method to minimize inhomogeneous effects due to inherent spatial information.

In the RBT transformation process, the image is viewed as a set of boxes or umbra (cubical pixels) in 3-D space (see Figure 1). The pixel and row number forms the umbra basis and ordinate while the pixel intensity is the height of the boxes. The ball being the structure element is moved freely on the umbra. The center of the ball is determined by the finding manima and then minima within the umbra of minima-template. The trajectory of the ball's center is the smoothed image. The transformation process is then repeated with the ball placed below the umbra surface for picking up the dimples; this process is known as opening. The closing is the former transformation process where the ball glides on the umbra. The opening and closing are the terms in mathematical morphology where the structural elements are used as operator to transform input pixel in an image according to the relationship of each pixel to other pixels in its neighbourhood. The structural element in the RBT is a sphere (ball). The opening of greyscale image X by structuring element Y is given by:

X_Y = [XQ Y] Å Y (1)

And likewide, the closing is given by :

X_Y = [XÅ Y]Q Y (2)

Where
Å is the Minkowski addition which is determined by translating Y by each element of X and then taking the unionof all the resulting translates; and
Q is the Minkowski subtraction determined by translating every element of Y by each element of X and then taking the intersection of all the resulting translation.

In this paper, the RBT was employed to produce two possible textural outputs : the smooth and rought components from the original input image. In both these intended outputs, the RBT was used as an estimae of the background level across a single grey level image. The smooth output is generated when the spikes and dimples are removed from the original image, and the other rough image is a combination of both spike and dimples. Both of these output components are textural components of the original input image, but their textural details are determined by the structuring ball size. As the size of the ball increases, wider spikes and dimples are separated from an increasingly smooth component. Thus, the RBT can systematically separate variations from the smooth components of an image.

To extract RBT textures, a program called BALL was written in the Microvax -4000 workstation. As our texture of interest was the land use categorical classes known to have varying degrees of variations among them, hence, various ball sizes were initially examined. Only four ball diameters (2,5,7 and 10) were found from visual analysis to have any significant delineation's among land use classes. Hence, these four ball diameters were chosen for extracting full texture of both study areas Plate 1(a) shows an example of textural output of RBT from 512x512 extract of band 5 of a test area using size 5. The smooth component of the RBT textural output for each ball diameter used was then further examined for their effectiveness in the classification of land use.

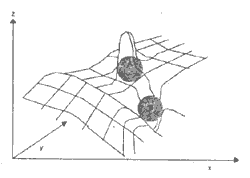
Figure 1: Schematic representation of the rolling ball transformation. The image form each spectral band is viewed as boxels. In the transformation process, the opening glides the ball on umbra, and closingglides the ball under the umbra following the background contours but does not penetrate the spike A or dimple B (modified after Strenberg 1986).
3.The Ripping Membrane (RM)
The RM was originally proposed by Blake and Zisserman (1987) as an algorithm for solving problem of finding discontinuities (edges) within an image. Unlike many methods of finding discontinuities such as Kernal high pass filter; the RM constitutes a powerful filter, able to detect even weak discontinuities and to localise them accurately with stability. As outlined by the concept of spectral signatures, each individual spectral class can be itemised by a unique spectral vector or digital number (DN) value and abrupt changes in the DN indicated a different type of class. In natural conditions due to the variations in nature (i.e. inherent spatial information), there will be clouds of points emanating from each class. Hence, in finding the vector to represent the class and to localise them have not proven to be simple problem with many kernel filter.

The RM employs the relaxation technique and is based on the analogy with a continuous elastic sheet which is capable, when stretched sufficiently, of ripping. The image is viewed as topography, the x and co-ordinates form the row and column number, while the DN values are the heights of the surface. Blake and Zisserman (1987) orginialy imagined this as an energy function. At each point ina given iamge, a spring is enchored to the height of the image on one end, while the other end is attached to the elastic sheet (Figure 2).

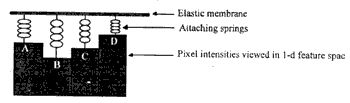
Figure 2: The ripingmembrane illustrated in 1-D. The A,B,C and D are pixel intensities, where the heights are directly proportional to theintensity vectors. The attaching springs are anchored to these points and the other spring -ends are attached to the elastic membrane (after Hashim, 1995)
The shape of the membrane at equilibrium will depend on the relative strength of spring traction and the elasticity of the membrane. Using the concept that a system at equilibrium will have minimum energy, then it is possible to calculate the equilibrium position of the membrane. Hence, the position of the membrane at equilibrium gives the estimation of smooth texture. It is however, possible to overstitch the membrane, as in the case where abrupt changes occurred (i.e. the interface of land and water), and at these junctions the membrane is allowed to rip (thereby reducing the energy).

Mathematically, the solution of such problem is complex. In general form, it the energy E needed for entire spring -membrane system at equilibrium over an interval of x where x [0,n] is given by Blake and Zisserman (1987) as:

E = D + S + P (3)

Where

P is the sum of penalities a accounted for every discontinuity; and
U is the position of the membrane.

Blake and Zisserman (1987) have proposed a solution depending on three factors; (I) how closely the membrane follows the original data (depends on strength of the spring). (2) the elasticity of the membrane (this indicates how well the membrane follows the local smooth average, and ignores individual departures); and (3) the ripping point where the membrane rips (this is where the contextual average can abruptly change). Various solutions can be found by varying these factors. In fact, solutions can be continuously varied from one that closely follows the intensity vectors, to one which follows the large scale average of the intensity vectors.

As the interest in this study lies in the detection of discontinuities that localize class regions, the ripping conditions in intensity were kept fixed, and the relative strength of the springs and the membrane elasticity were varied. Thus, only one parameter, referred to as the range was varied in this study. A large range gives more stiffness to the membrane over the strength of the spring, hence, the solution reflects the contextual average. Similarly, a smaller range will give a solution which fellows more closely the intensity vectors. Subtracting the resultant solutions of the membrane from the original image gives the image portraying the local variations, where the size of the local variations are determined by the chosen range. The smooth solutions, are, however, the main concern in this study. The main inanition is to use RM as a means for estimating the minimized variations caused by spatial information.

In implementing the RM technique, a program based on Graduated Non-Convexity algorithm (GNC) was the Microvax-4000 image processing system. The parameter range that best represented the overall textures was investigated. The range parameters of ,5,7,10,30 and 40 (in unit pixels) were tested in this study. For every range, all the TM band were independently processed with the RM transformation. In effort, the RM technique, replaced the DN value of a pixel by a value which was proportionally closer to the average of DN value of its replaced the DN value of a pixel by a value which was proportionally closer to the average of DN value of its neighborhood. If a difference was larger than the range value (which acts as a threshold), the original DN value was left unaltered. The process was iterated until no pixel in the image changes value (i.e. converges). The smoothed RM values of the corresponding features were then incorporated into the classification process. Visual examples of RM solution using ranges 5,10 and 20 are shown in plate 1(b).

4.Application Test

4.1Study Area
A total of 13 land cover types, namely the agricultural land use classes of a Landsat TM subscene (1024 x 102) over Bruas, Malaysia was tested in this study. The land-use map were digitised and rasterized to the equivalent image spatial resolution. The image data were later geometrically -corrected by registering the prominent points in the image to the corresponding features in the digitized land use map.

4.2Textural Extraction and Evaluations
Five textural measure were used to derive the textural information from all spectral bands for the study area. These include the GLCM, LST CFM, RBT and RM. To analyses whether or not, textural information improves classification accuracy, two classification only the textural information derived from each of the six TM bands. The second was the classification of the combination of the best textural information derived from each of the six TM bands. The second was the classification of the combination of the best texture with the original data. Only the best texture measures, selected from the first classification set, were used in the second classification sets. As such, in the second classification set, a total of 14 features were used for every classification tested.

The classification were carried out the combined unsupervised /supervised maximum likelihood, and the watershed method. These two classification methods have been earlier described in great detail in Hashim et. Al., 1985. For each study-area, a total of 128 classified images were produced in the first classification set , where they are classified from a total of 364 textures produced. Four classified images were projected in the second set. Table 1 summarises how these textural features were derived.

In evaluating the classification accuracies, the land use labels (ground truth) were used with the object labeling program. The labelling program divides the image into two random mutually exclusive set: one the training set and the other the test set. The training set allows the spectral classes to be translated into ground truth labels for each classified image. The test set was then used to evaluate the accuracy for each method. An error matrix was produced for analysing the overall average accuracies for each classification image. The kappa coefficient of agreement (Hudson and Ramm, 1987) for the test classification set was also computed.

5. Results
Results of classifying using textural information alone (first classification set) is summarised in Table 2, while the classification accuracy with the combination of textural and raw data (second classification set) is tabulated in Table 3.

The two new methods proposed the RBT and RM gives the most stable textural outputs. Textures derived by each of these two methods, although dependent on window size, the changes were rather gradual compared to the GLCM texture. The RM 20 give the best overall classification accuracy in both area for both classification methods tested. The best classification using the combination of raw data and RM20 for the study area (Plate 1-c). The combined spectral and textural of RBT and RM texture, however, were still ineffective in improving accuracies for classes 1u, 2h, 3x, 4c, and 6 (please refer Table 2 for classes descriptions) where only accuracies of less than 50 per cent were attained. This could be attributed to the in appropriate size of the window used. Since each of these classes (1u, 2h, 3x, 4c, and 6) has clear spatial structure, spatial window sizes in this study were probably too bit to generalise the fine spatial details that characterise these classes.
Table 1. Sumamry of textural derived, classified and analysed for NLUC maping. Item (a)-(e) are the first classification set produced by classifying individual textures alone, and (f)-(k) are the second classification set. A total of 378 textures derived were for each study site where 128 first and 6 second classification are anyalysed, respectively. Please refer text for descriptions of classification sets. Combination of textural and raw data:


Textural derivation methods	window or range size (unit pixel)	No. of features used	No. of textures derived	Texture* abbreviation

(a)	spatial grey level co-occurrence matrix (GLCM)	3,7,11,21
	Angular second moment		7	28	ASMw
	Contract		7	28	CONw
	Entopy		7	28	ENTw
	Inverse difference moment		7	28	IDMw
	Sum of entropy		7	28	SEw
	Difference of entropy		7	28	DEw
	Difference of variance		7	28	DVw
(b)	Local statistical transform (LST):
(b)	Median filter	7,11,21	7	21	MEDw
(c)	Convolution filtering mask (CFM):
	Thmas et. Al (1987) textural mask	3	7	7	THOM
	Ford et. Al. (1983) textural mask	3	7	7	FORD
(d)	Rolling ball transformation (RBT):	2,5,7,10	7	28	RBw
(e)	Ripping membrane (RM)	2,5,7,10	7	49	RMw
		20,30,40

(f)	The best of GLCM and raw data	11	7	14	DVII-plus
(g)	The best of medium and raw data	7	7	14	MED7plus
(h)	The best of RBT and raw data	5	7	14	RB5-plux
(i)	The best of RM and raw data	20	7	14	RM20plux
(j)	All the best texture from each category			56	TEXT
(k)	All the best textures and raw data			63	TEXt-plus

*note: the letter w at the end of texture abbreviations indicate the corresponding window size where the textural information are derived from

7. Conclusions
In this paper, two new textural extraction methods from spectral data for its utility to improve image classification for land use classes were examined. Comparative analysis were also carried out against three commonly used texture measures : (1) GLCM textures namely the angular second moment, contrast, entropy, inverse difference moment, sum entropy different entropy and difference entropy and difference variance; (2) local statistical transformation using median filter; and (3) convolution filtering masks employing the 3x3 and 5x5 textural templates, respectively. Textures were derived to cover both the micro-tomcat textures. For each texture. For each texture derived from the original TM bands, two classification sets were produced. The first was based purely on the textural information and the second used a combination of textural and raw data.

Textural information as illustrated in this paper was one of the possible methods to increase the classification accuracies of the land use classes. The best results were obtained when textural information was combined with raw data. The best GLCM was the difference of variance extracted from an 11x11 window. The new textural approaches-the RBT and RM showed the most stable textures. RM textures from range 20 was the overall best textural methods.

The combined spectral/spatial classification data indicated that the degree of accuracy improvement varies from class to class, suggesting different spatial dependencies for each class. Thus, one best texture within the selected window size may be good for one class but not others. Where many classes, such as the 13 classes of the land use as the Markov random field (Zhang and Chen, 1988; Geman and Geman, 1984) is recommended.

References

Blake, A., and Zisserman, A., (1987), Visual Reconstruction. (London : The MIT Press)
Ford, G.E., Algazi, V.R., and Meyer, D.I., (1983), A non-interative procedures for land-use determination Remote Sensing of Environment, 3:1-16.
Geman, S., and Geman, D., (1984), Stochastic Relaxation, Gibbs Distributions, and the Bayesian restoration of image,. Visual System architectures, IEEE PAMI, 6(6), 721-741.
Haralick, R.M. Shanmugam, K.S., and Dinstein, I., (1973), Textural and image classification. IEEE Transactions on systems, man and cybernatics, SMC-3, 610-622.
Hashim M., (1995) Classification of Landsat Mapper data for Land Cover Mapping in Malaysia: a Morphological and Contextual Approach. Ph.D. Thesis (Unpublished), Dept. of Environmental Science, University of Stirling, United Kingdom.
Hashim, M., Watson, A., and Thomas, M. (1995), Image Classification with Higher-dimension Watershed Classifier. Proceedings of the 21st. Annual Conference of the Remote Sensing Society, 11-14 September 1195, Southampton, United Kingdom, 1204-1211.
Hudosn, W.D., and Ramm, C.W. (1987), Correct formulation of kappa coefficient of agreement. Photogrammetric Engineering and Remote Sensing , 53(4): 421-422.
Sternberg S.R., (1983), Biomedical image processing computer. IEEE Computer Society, 6:22-34.
Sternberg, S.R., 91986), Greyscale morphology, Computer Vision, Graphics, and Image Processing, 35,333-355..
Thomas, I.L., Benning, V.M., and Ching, N.P., (1987), Classification of Remotely Sensed Images (Bristol: Adam Higler), 268p
Zhang, M., and Chen, S., (1988), Spatial information processing : Understanding remote sensing imagery in Chen, S. (eds.) Image understanding in unstructured environments. (Singapore : World Scientific), 179-208.

Table 2. The overall classification accuracy (per cent ) of NLUC classified using only textural features (first classification set). Entries given by '-' are featureless texture due no probabilities computed. Please refer Table 1 for texture descriptions. Features selected for the second classification set is denoted by * in the remark column.

B-area
	Watershed	Maximum
Textures	method	likelihood	Remarks
ASM3	23	3
CON3	3	3
ENT3	24	10
IDM3	-	-
SE3	35	14
DE3	-	-
DV3	30	14
ASM7	27	3
CON7	23	15
ENT7	11	13
IDM7	17	15
SE7	38	12
DE7	20	10
DV7	32	12
ASM11	35	15
CON11	38	13
ENT11	27	11
IDEM11	38	14
SE11	39	15
DE11	38	13
DV11	40	12
ASM21	13	3
CON21	23	3
ENT21	11	14
IDM21	17	15
SE21	18	15
DE21	20	14
DV21	18	14
MED7	12	12
MED11	12	12
MED21	14	12
THOM	12	11
FORD	12	16
RB2	37	15
RB5	40	16
RB7	77	16
RB10	34	16
RM2	36	16
RM5	38	16
RM7	39	16
RM10	40	16
RM20	41	18
RM30	40	18
RM40	39	18

Plate 1: Textures produced by the rolling ball transformation illustraed using 512x512 extract of test-area with ball size of 5 (unit pixels).(a) Raw TM band 5, (b) the dimples, (c) the pimples, (d) the rough components and (e) the smooth components.