On the Architecture of layered Neural Network for Land use Classification of Satellite Remote Sensing Image

On the Architecture of layered Neural Network for Land use Classification of Satellite Remote Sensing Image

Shimizu, Eihan and Le, Van Trung
Deparment of Civil Engineering, University of Tokyo
7-3-1 Hongo, Bunkyo-ku, Tokyo, Japan
Tel : 03-3812-2111 ext. 6126 FAX : 03-3812-4977
E-mail : trung@planner.t.u.tokyo.ac.Jp

Abstract
Layered Neural Network (LNN) have been proposed recently as a non-parametric classification method suitable for the efficient analysis of satellite remote sensing images. Most of the studies in this field, however, have been empirical and LNNs have been applied just like "black box" estimation machines. When a non-parametric function is trained with {0,1} binary target by the least squares, the output of the calibrated function is considered an estimate of a posterior probability. The accuracy of this estimate mainly depends on the network structure, the activation function form as well as he learning paradigm and the number of training data sued in learning. This paper discusses the application of LNN to remotely sensed data classification. We provide a theoretical interpretation for the LNN Remotely Sensed Data Classification. We provide a theoretical interpretation for the LNN classifier in comparison with the conventional classification methods. The most important part is the derivation of a generalized form of LNN classifier based on the maximum entropy principle. According to the generalized form, we discuss the relationship between the familiar type of LNN classifier employing the igmodial activation function and the other types of discriminate models such as the Multinomial Logit Mode.

1. Introduction
Layered Neural Networks (LNN) have been broadly applied in classification, prediction and other modeling problems. Hill et al.. (1994) gave a full review of studies comparing LNNs and conventional statistical models. With the exception of comparisons with regression analysis, however, there have so far been few studies to provide a theoretical interpretation for the application of LNN.

This paper will show how LNNs approximate the Bayes optimal discriminate function when used for classification of satellite remote sensing image, and discuss the relationship between the familiar type of LNN classifier employing the sigmodial activation function and the other types of discriminate models such as the Multinomial Logit Model.

2. Basic Formulating of LNN Classifier
Let x represent a feature vector which is to be classified. Let he possible classes be denoted by wj(i=1,2.J). If we consider the discriminate function dj(x), then the decision rule is

x Îw_j, if d_j(x)³d_j 9x) for all j'¹j. (1)
An LNN is expected to be the I/O system corresponding to the discriminate functon.

Let us consider the multi-layered neural network in the figure 1 which has been applied to a variety of classification problems.

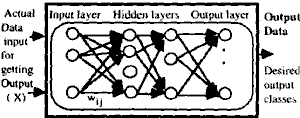
Figure 1
A feature vector is input to the input layer; that is, the number of neurons in the input layer corresponds to the dimension of the feature vectors. The number of neurons in the hidden layers can be adjusted by the user. The output layer has the same number of neurons and the classess.

The output signal from the jth neuron in the output layer is regarded as the discriminant value. Let the state of the jth output neuron be represented by

u_j = g(x,w) (2)
where w is the parameter vector which is mainly constituted by the connection weights between neurons. We are not concerned here with the fomulation of g(x,w). The output of LNN. Pj(x,w) under presentation of x is

p_j(x,w) = f(u_j), (3)
where f(uj) is the activation function. The following sigmoid function. The following sigmoid function is frequently used,

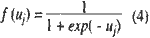
The feature vectors xk(k=1,2,…K) for training the LNN are prepared.

Training data (target data) are given as follows:

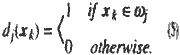
the LNN is trained (Fig. 2) by minimizing a mean squared errors, that is,

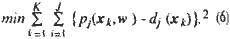
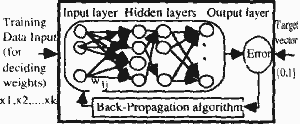
Figure 2
Training of the LNN is performed thrugh the adjustment of connection weights. The most common method is so-called "back-propagation" which is essentially gradient descent. After the completion of training, the LNN plays a role of the discriminant function, Let the output of trained LNN be denoted Pj(x,w)

3. Interpretation for LNN Classifer

3.1 Relationship between LNN and Bayesian classifer
The Bayesian optimal deision rule minimizes the probability of classification error by choosing the class which maximizes the posterior probability:

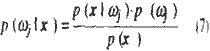
If the prior probabilities p(wj) are equal, then the conditional probability density function p(x | wj) corresponds to the optimal discriminate function. Maximum likelihood classifier, in which a multivariable normal distribution is assumed, is frequently applied.

The question of how the LNN classifier is related to the Bayesian optimal classifier has already been discussed by Wan (1990) and Ruck et al. (1990). The conclusion is that the output of the LNN, pj(x,w), when trained by the criteria (6), approximates the Bayesian posterior probability. In accordance with Wan (1990), we show a short proof. Consider the training data given in the form of (5). Suppose that the training data are random variables and samples from the probability density function p (x,dj(x), where

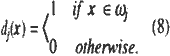
Since pj (x,w) is the least squares estimate of dj(x), then pj(x,w) is the conditional expectation of dj(x) given x. therefore

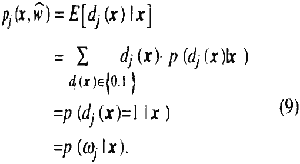
This means that pj(x,w), in the sense of mainimizing a mean squared error, approximates the posterior probability p(wj|x). Therefore, output of the LNN is considered an estimate mainly depends on the network structure, the activation function from as well as the learning paradigm and the number of training data used in learning. This is a theoretical background of the application of LNN into classification problem. It is also proved that a three-layered neural network, when the appropriate number of neurons are set in the hidden layer and sigmodal ctivation function are used in the hidden layer, can approximate any continuous mapping (e.g. Gallant eta l., 1988; Funahashi, 1989; Cybenko, 1989; Hornik et al., 1989). It is expected that an LNN approximates fairly accurately the posterior probability if the user chooses the right size of network, the appropriate number of training data, the stopping criterion of learn inland the appropriate form of I/O function.

Up to this point, however, the derivations have been for an arbitrary mapping trained by dj(xk)Î{0,1}. The result is well-know in the field of statistics (Wan, 1990). The above proof provides a theoretical justification for any non-parametric discriminate function trained by the least squared criteria. The following section willdiscuss the interpretation for the activation functions used in LNN.

3.2 Interpretation for activation functions
Let the activation function, f(uj), be a monotonic increasing function. Then, the state of the output neuron, uj, and the posterior probability, p(wj|x), have a one -to-one mapping, and uj = g(x,w) become also an optimal discriminate function.

The activation function should be a probability distribution given a certain level of state. This is analogous to the probability distribution of a particle being in a certain state given the energy level of each state in the statistical mechanics. In statistical mechanics different probability distributions are derived from so-called maximum entropy principle. We derive the activation function forms from this principle.

Consider the maximization of Kapur's generalized measure of entropy under the expected discriminate value (Kapur. 1986)

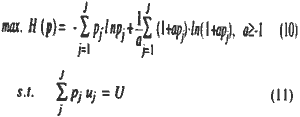
where H(p) s Kapur's generalized entropy in which the constant term is omitted. pj(j=1,2..J) is a probability distribution corresponding to pj(x,w), a is a parameter prescribing the type of entropy, that of entropy, that is, the type of probability distribution, and U is an expected discriminate value. Here, we do not explicitly give the constrant;

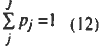
to the maximization problem, because pj approximates the posterior probability, From (10) and (11), we get

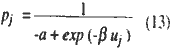
where b is a Lagrange multiplier associated with (11). The parameter b is the so-called temperature parameter by which the slope of the activation function. When a is fixed and the LNN with the activation function (13) is trained, the estimation of b is included in the conncection weights in a training process, since uj is generally defined by the linear function of the connection weights between the output neuron concerned and the hidden nuron.

Now, assume that b is constant, the probability distribtution (13) is equivalent to an optimal solution of the following maximization (Brotchie, 1979);

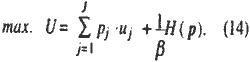
Therefore, the activation function from 913) is interpreted as the representation of the above expected discriminate value maximization taking into account the uncertainty shown as Kapur's entropy.

Now, let us return to the activation form 913) and discuss the meaning of the parameter a. For a = -1 (13) gives;

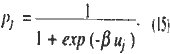
This is just the sigmoid function (i.e., (4)) most frequently used in the applications of LNNs. In addition, if a=-1, it is well-known that (10) subject to (11) and (12) gives Femi-Dirac (F-D) distribution. Note that pj(x,w) approximates the posterior probability; thus the familiar sigmoid function is interpreted as the representation of the expected discriminant value maximization under the F-D type entropy. Similarly, for a=1. (13) is

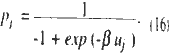
It is known that, for a=1, (10) subject to (11) and (12) gives Bose-Einstein (B-E) distribution. Thus 916) approximates the B-E Distribution.

Next, consider the case of a = 0, that is

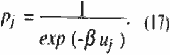
As a tends to zero, (10) approaches Shannon's measure of entropy. It is well-known that the maximization of Shannon's entropy subject to (11) and (12) gives Maxwell-Boltzmann (M-B) probability distribution;

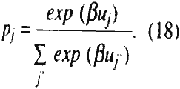
Accordingly, (17) approximates the M-B distribution. In addition, (18) given the structural similarity with so-called Multinomial Logit Model which is familiar in the field of the discrete choice behavioral modeling (Anas, 1983). Hence the LNN classifier with activation function (17) is interrelated as the approximation of the Multinomial Logit Model.

As a mentioned above, the choice of a = -1,0 and 1 leads to Fermi-Dirac (F-D), Maxwel-Boltzmann (M-B), and Bose -Einstein (B-E) statistical mechanics. Let us compare the characteristics of the above representative distributions in statistical mechanics. These three distributions in statistical mechanics. These three distributions are all derived from Jaynes's maximum entropy principle (Kapur, 1992). One distributions differs from another due to the constraints to Shannon's measure of entropy, In the M-B distribution, the expected energy of a particle in the system is only prescribed. The F-D and B-E distributions are derived by the constraints with respects to the expected energy of the system and the expected number of the particles in the system. In the F-D distribution the maximum number of the particles allowed in a certain state is assumed to be one, while in the B-E distribution the maximum number is assumed to be infinite.

Thus, the paramter a is associated with the constraints to the maximization of the Shannon's entropy. This suggests that, for a lying between -1 and 1, we can get the various types of probability distribution, though it may be difficult to rovide the significant interpretation for the distributions within the framework of statistical mechanics. We have a choice of infinite types of models corresponding to different values of a. A possible method is to choose the parameter a to get the best fit to the training data. Regardless of the selected parameter, we can provide the interpretation to the acivation function as the interpretation to the activation function as the representation of the expected discriminant value maximizationunder the Kapur's generalized entropy.

4. Conclusion
This paper has provided an interpretation for the LNN classifier. The output of the LNN under the completion of training approximates the Bayesian posterior probability. Therefore, if we assume the activation function of the output neuron to be monotonic increasing, the state of the output neuron is also Bayesian optional discriminant function .

The maximization of Kapur's generatized measure of entropy gives the generalized form of the probability distribution including the Maxwell-Boltzmann, Femi-Dirac, and Bose-Enstein Distributions. From the maximum entropy principle, we can provide the interpretation for the activation function. The familiar sigmoid function is approximate to the Fermi-Dirac distribution. The approximate to the Fermi-Dirac distribution. The LNN classifier using the activation function of the Maxwell-Boltzmann distribution approximates the Multinomial Logit Model.

In th practical sense. It is proposed that we apply Kapur's generalized distribution to the generalized distribution to the generalized activation function and fix the function form in the process of training. Regardless of the resulting selected function form, we can provide the interpretation for that as the representations of the maximization of the expected discriminate value under Kapur's generalized entropy.

References

Anas, A. (1993) Discrete Choice theory, information theory and the multinomial logit and gravity model. Transportation Research, Vol. 17B., No. 1, 13-23.
Brotchie, J.F. and Lesse, P.F. (1979) A unified approach to urban modeling. Management Science, Vol. 25, No. 1, 112-113.
Funahashi, K. (1989) on the approximate realization of continuous mapping by neural networks. Neural Networks, Vol. 2, 183-192.
Gallant, A.R. and White, H. (1988) There exists a neural network that does not make avoidable mistakes, Proc. Int. Conf. Neural Networks 1 (July, 1988), 657-666.
Hill, T., Marquez, L., O'Connor, M. and Remus, W. (1994) Artificial neural network models for forecasting and decision making. Int Jour. Forecasting. Vol. 10m5-15.
Hornik, K.M. Stinchcombe, M. and White, H. (1989) Multiplayer feed forward network are universal approximators. Neural Network, Vol. 2, No. 5, 356-366.
Kapur, J.N. (1986) J.N. (1986) Four families of measures of entropy. Ind. Jour. Pure and Applied Mathematics, Vol. 17, 429-499.
Kanpur, J.N. and Kesavan, H.K. (1992) Entropy optimization principles with application Academic Press, Inc., 77-97.
Ruck, D.W., Roger, S.K., Kabrisky, M., Oxley, M.E. and Suter, B.W. (1990) The multiplayer perception as an approximation to a Bayes optimal discriminate function. IEEE Transactions on Neural Networks, Vol. 1, No. 4, 296-298.
Wan, Eric A. (1990) Neural network classification: a Bayesian Interpretation IEEE Transaction on Neural Networks, Vol. 1, No. 4, 303-305.