| GISdevelopment.net ---> AARS ---> ACRS 1997 ---> Digital Image Processing |
Sattelite Image Data
Compression using Vector Quantization on Wavelet Information
S. Wongkharn, M.
Chongcheawchamnan
Faculty of Engineering mahanakorn University of Technogogy
Bangkok 10530, Thailand
K. Kittayaruasiriwat, F. Cheevasuvit, K.Dejhan
Faculty of Engineering, King Mongkut's Institute of Tecnology ladkraband
Bangkok 10520, Thailand
Abstract Faculty of Engineering mahanakorn University of Technogogy
Bangkok 10530, Thailand
K. Kittayaruasiriwat, F. Cheevasuvit, K.Dejhan
Faculty of Engineering, King Mongkut's Institute of Tecnology ladkraband
Bangkok 10520, Thailand
The application of wavelet transform on an image results subband images. These subband images compose of a low-pass subband image (approximation image) and three high-pass subband images (detail images). We can apply the vector quantization (VQ) on these high pass subband images to compress image data. But this technique loses some edge's details. Since the edges of image are important for the sattelite image processing such as an image interpretation and an image classification. Therefore, this paper presents a settelite image data compression technique using vector quantization on wavelet subband image by maintaining the edge's details. The proposed technique gives more gradient informations which relate to the information details of the edges.
(1) Wavelet Transform
Wavelet transform (WT) in the image processing can be considered as a subband decomposition [1],[2],[3]. Fig. 1(a) shows an image wavelet decomposition diagram. The original image fL (x,y) is firstly filtered on the row by applying filter H and G and downsampled by keeping one column out of two. Two resulting images, the low-pass fL (x,y) and high-pass fH (x,y)outputs are obtained. Then, both of them are filtered along the column and upsampled by keeping one row out of two. It can be obtained one low-pass subband image denoted by fLL (x,y) and three high-pass subband images denoted by fLH (x,y), fHL (x,y) and fHH (x,y, respectively. The image fLL (x,y) is a dc component while the other threes are image's edge information. Finally, the image wavelet reconstruction is show in Fig. 1 (b)
(2) Vector quantization
Vector quantization (VQ) [4] is a lossy compression technique. This technique is composed of two part, encoder and decoder and decoder. An encoder will compare each input vector with every code vector in the codebook and generate index which represent the minimum distortion code vector from the input vector. A decoder takes the indexs to locate the codevector in the codebook and generate the output vectors.
A codebook is the set of finite codevector for representing the input vectors. The popular technique in codebook design is the Linde-Buzo-Gray (LBG) algorithm [5],[6].
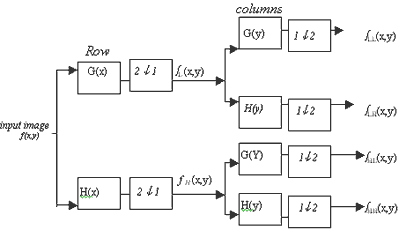
(a) image wavelet Decomposition
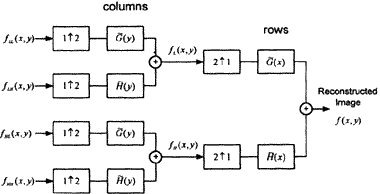
(b) Image Wavelet Reconstructed

Fig.1 Image Wavelet Transform and Its Inverse
(3) Image Compression using Vector Quantization on Wavelet Informations
Firstly, the wavelet decomposition is applied to the original image and results wavelet sub band images. These sub band images are coding by vector Quantization using each sub band's codebooks. These codebooks are called mutiresolution codebooks. Fig. 2 (a) shows the image compression and Fig. 2(b) shows the image decomposition. The principle method of this technique is bit assignment for each sub band besed on the energy in that sub band. The higher energy sub band is encoded by using higher bit rate.
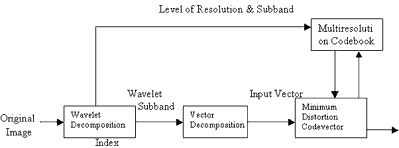
(a) Image Compression
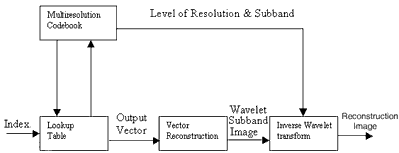
(b) Image decompression
Figure 2 Image compression and decompression using VQ on wavelet informations
The application of vector Quantization on wavelet information is an image compression technique introduced by [7]. For the traditional method of bit assignment is shows in Fig. 3. By using this technique, the sub band HH is discarded. This causes the image loses some details. Thus, a new scheme of bit assignment in Fig.4 is proposed to maintain the edges of image.
| LLLL | LLHL | HL |
| LLLH | LLHH | |
| LH | HH | |
(a) Subband images
| 8 bpp | VQ 2 bpp Codebook size=2*2 N=256 |
VQ 0.5 bpp Codebook size=4*4 N=256 |
| VQ 2 bpp Codebook size=2*2 N=256 |
VQ 0.5bpp Codebook size=4*4 N=256 | |
| VQ 0.5bpp Codebook size=4*4 N=256 |
0 bpp | |
(b) Bit assignment
Fig. 3 Traditional method at bit rate = 1.03125 bpp
| LLLL | LLHL | HLLL | HLHL |
| LLLH | LLHH | HLLH | HLHH |
| LHLL | LHHL | HHLL | HHHH |
| LHLH | LHHH | HHLH | HHHH |
(a) Subband images
| 8 bpp | VQ 2 bpp Codebook size=2*2 N=256 |
VQ 0.5bpp Codebook size=4*4 N=256 |
VQ 0.5bpp Codebook size=4*4 N=256 |
| VQ 2bpp Codebook size=2*2 N=256 |
VQ 0.5bpp Codebook size=4*4 N=256 |
0 bpp | VQ 0.5bpp Codebook size=4*4 N=256 |
| VQ 0.5bpp Codebook size=4*4 N=256 |
0 bpp | 0 bpp | VQ 0.25bpp Codebook size=4*4 N=16 |
| VQ 0.5bpp Codebook size=4*4 N=256 |
VQ 0.5bpp Codebook size=4*4 N=256 |
VQ 0.25bpp Codebook size=4*4 N=16 |
VQ 0.5bpp Codebook size=4*4 N=256 |
(b) Bit assignment
Fig. 4 Proposed method at bit rate = 1.03125 bpp
4. Experiment Result
Two 512*512 satellite, JERS-1 and Landsat, gray images are used in this experiment on a PC. Fig.5(b) and 6(b) show the compressed images using the traditional method and them gradient images are shown in Fig. 5(c) and 6(c), respectively. Fig. 5(d) and 6(d) show the compressed images using the proposed method and them gradient images are shown in Fig. 5(e) and 6(e), respectively. The comparison Results show that the proposed method gives lesser MSE and more average gradient. This can confirm by following table.
| Traditional method | Proposed method | |||
| MSE | Average gradient | MSE | Average gradient | |
| JERS-1 | 60.1278 | 111.4997 | 55.3232 | 114.6669 |
| Landsat | 47.6863 | 86.3965 | 44.2886 | 89.0453 |

Figure 5: Resulting image of JERS-1 imagery

Figure 6: Resulting image of Landsat imagery
Since the gradient information relate to the details of image , so that means the proposed methods gives more details of image.
5 Conclusion
The experimental results show that the image compression using vector Quantization on wavelet information be the proposed method can reduce MSE and maintain the edge's details. Therefore this technique is useful for satellite images, which need the edge's details for interpretation and classification.
Acknowledgement
The authors would like to thank the National research Council of Thialand for providing the satellite images.
References
- P.M. Bentley and J.T.E. McDonnell, "Wavelet Transform: an Introduction," Electronics & Communication Engineering Journal, August 1994.
- R.K. Young, Wavelet Theory and Its Application, Kluwer Academic Publishers, 1993.
- S. Mallat, "A Theory for Multiresolution Signal Decomposition: The Wavelet Representation," IEEE Trans. On Patt. Anal. Machine Intell., Vol.11, No.7,pp. 674-693 1989.
- N.M. Nasrabadi and R.A. King, "Image coding using vector Quantization: A Review," IEEE Trans. Commun., Vol. COM-36,p.957-971, Aug. 1980.
- Y. Linde, A. Buzo, and R.M. Gray, " An Algorithm for vector quantizer design," IEEE Trans.Commun., Vol.COM-28, pp.84-95, Jan 1980.
- A. Gersho and R.M. Gray, Vector Quantization and Signal Compression, Kluwer Academic Publishers, Boston, 1992.
- M. Antonimi, M. Barlaud, P. Mathieu and I. Daubechies, " Images coding using wavelet transform," IEEE Trans. On Image Processing, Vol.1, pp. 205-220, April 1992.