Electromagnetic Scattering from Foliage and Vegetation: Modelling and applications in Active Microwave Remote Sensing

Electromagnetic Scattering from Foliage and Vegetation: Modelling and applications in Active Microwave Remote Sensing

H.T. Chuah
Faculty of Engineering
Universiti of Engineering
Jalan Ayer Keroh lama
75450 Melaka
Tel: +606-2523456; FaxL +606-2316552
E-mail: htchuah@unitele.com.my

Abstract
This paper aims to review some theoretical models for electromagnetic wave-matter scattering and propagation in foliage and vegetation that have been developed for the past ten years or so. These include models using the Renormalization Technique (a field approach); the Radiative Transfer Theory (an energy/intensity approach) and models using the Monte Carlo technique (a statistical method). Various examples are given to illustrate the potentials of these methods: study of propagation of wave in a vegetation canopy to calculate the effective attenuation coefficient, and radar backscatter from a vegetation field/forest stand. The simulated results are compared with experimental data wherever possible to validata the models.

Introduction
Electromagnetic scattering and propagation in foliage and vegetation is a complex vector problem because of the multiple scattering between a mixture of randomly distributed components of the medium, including the ground surface. The task of modeling a complete vegetation medium must include all the interactions between the separate components of the vegetation, including the soil. Various volume and scattering theories have been developed for modeling the scattering and propagation in such random media [1]. Basically, there are three main approaches: the field approach, the energy/intensity approach and the statistical approach. In the past ten years, some research work has been done in Malaysia to develop models based on such formulation. This paper aims to give an overview of those models developed, together with some results and comparisons with experimental data.

2. High-order Renormalization Method (HRM)
In this field approach, the vegetation medium is characterized by a complex permittivity function:

e(r) - e_a + e_f (r) ...(1)
where e_a and e_f are the average and fluctuations of the complex permittivity of the random medium. The vector wave equation for the electric field E in the medium is then written as:

(Ñ*Ñ*-k_o²e_a)E=LE= k_o²e_f =xE ……………….(2)
By separating the electric field E into the mean field Em and the fluctuating field Es, and assuming center-valued Gaussian statistics for the fluctuations in the random medium, we obtain:

(L-(xL^-1x))E_m =-(xL^-1xE_s) and LE_s =xE_m +[xE_s - (xE_s)] ..(3a)and(3b)
To solve for the mean field Eq. (3) is iterated starting with E_m=E^o_m and E_s=0. After some manipulation, for second order iteration, we have:

(L- (xL^-1x))E²_m =0 and LE²_s = x))E^o_m + xL^-1xE^o_m - (xL^-1x)E^o_m ..(4a)and(4b)
The basic approach is to find a good approximation for the mean field E_m from which the scattered field is then determined from Eq. (4b). The mean field is governed by theDyson equation, which can be conveniently respreseted by Feynman Diagram:

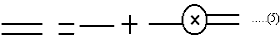
where

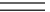represents the mean field,

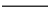the half space Green's dyadic and the mass operator

represents an infinite series of strongly connected terms,

in which

represents the correalation between r and r' as given by the product (x(r)x (r')).

By only selecting the first three terms of the mass operator, we are able to solve the Dyson equation of the form:

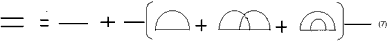
Eq. (7) gives a mean field improved by the two additional infinite series compared to bilocal approximation where only the first term of the mass operator is considered. Using the improved mean field, the second order scattered field E²_s and the radar backscatter coefficient can be calculated. Figure 1 compares the results of the calculations using both the mean field based on bilocal approximation and the HRM. We note that the results from HRM give a much slower drop at large incident angles, a trend that agrees with data from experiments. Figure 2 shows a typical comparison with experimental data for soyabean at 7.1 GHz.

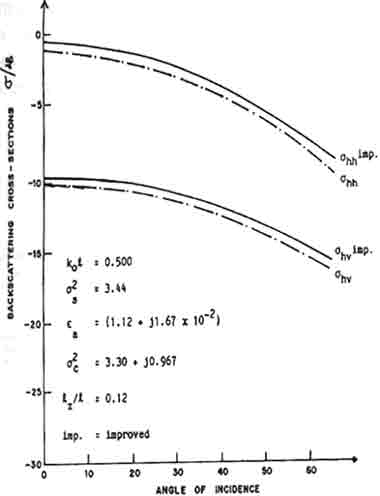
Fig. 1: Comparison between bilocal and HRM mean field Renormalization Method

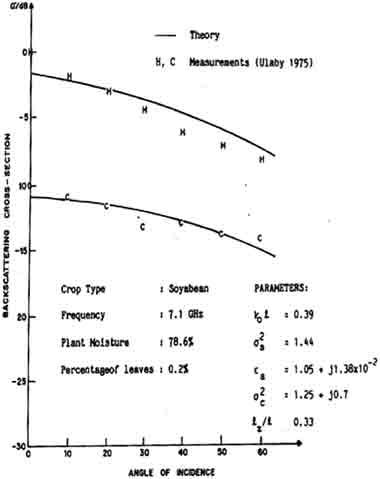
Fig.2: Comparison between HRM and experimental data for soyabean at 7.1 GHz
3. Radiative Transfer Approach
Consider the problem of a plane wave in air incident onto an inhomogenous layer above a place ground half-space (see Figure 3). The equation of energy transfer describing the Stokes' intensity vector, I, within the layer can be written as:

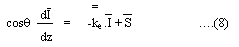
where ke is the extinction coefficient matrix and S the source term arising from energy scattered from other directions into the direction of propagation by scatterers in the medium given by:

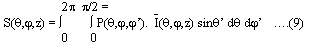
P is the phase matrix of the scatterer in the medium. This formulation is extended to study a vegetative consisting of mixture of different types of scatterers. A set of equations for iteration can be obtained by substituting the boundary conditions into Eq. (8). After the equation is solved the backscattered coefficient can be calculated using the backscattered specific in the air.

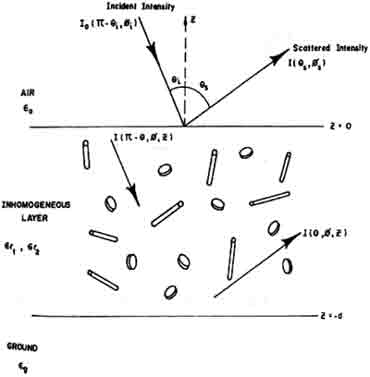
Fig3. Scattering Model for an inhomogeneous Layer Above a semi-infinite planar half-space
Figure 4 gives an example of comparison with measurement from a soyabean field where the canopy height is about 1.0 m. The field is modeled as a layer of circular disks, representing the leaves; and prolate ellipsoids representing the stems. Good agreement is obtained between measurement and theory for both co-and cross-polarizations except near nadir where the contribution from surface is significant. For simplicity, the soil surface has been modeled as a plane. To treat rough surface effect, a rough surface model can easily be included in the model.

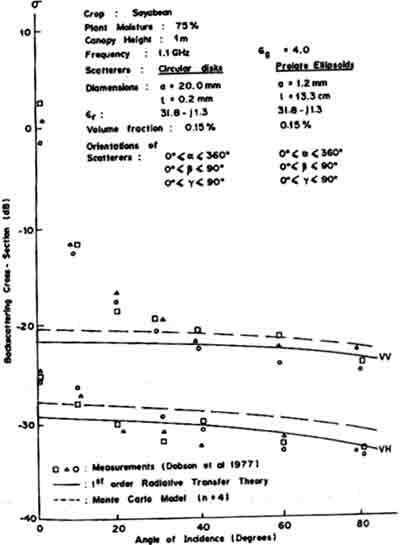
Fig.4 Comparison of Radiative Theory and measurements from soyabean field at 1.1 GHz
4. Monte Carlo Modesl
The Monte Carlo technique is statistical method of solving mathematical and physical problems by simulation of random quantities. It is particularly suitable for application to a class of physical problems that requires precise calculation of energy transport, taking into account a detailed radiation model of the medium and the multiple scattering processes and energy transfer in the medium. In this method, the multiple scattering processes in the random medium are treated as chains of collisions between the photons in the incident beam and the discrete scatterers. At each scattering event, a probability function in assigned to the following possibilities:

The probability that a photon is scattered or absorbed,
The probability that photon encounters a particular type of scatterer in the midst of various types of scatterers.
The probability that the orientation of the scatter is described by the Eulerian angles,
The probability that a photon incident from direction W' is scattered into a new direction W.

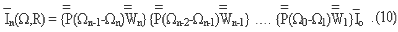
The process is described the following equation:

Where In is the Stockes' vector of a particular photon that has arrived at the receiver R in the direction W after undergoing n collisions. P, W are the phase matrix describing the scatterer and the combined biasing probability matrix of the collision.

By using sufficient number of photons, an ensemble average of In can be obtained. Effective Attenuation coefficient Kq in the random medium can be calculated using the definition,

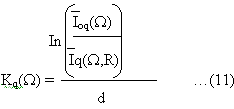
where Ioq and Iq are the incident and the transmitted intensity with q polarization, respectively, and d the distance traveled.

Similarly the backscatter coefficient s pq can be obtained using the definition:

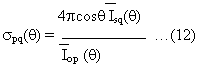
Figure 5 shows the comparison of vertically polarized normalized cross-sections for different cylinder radii at 9 GHz. The Monte Carlo model is able to give values that match well with experimental data, both in trend and in value. Figure 6 contains the comparison of backscatter coefficient from Monte Carlo model and measurement from Japanese Cypress. Close agreement is obtained for both cases: one with leaves and one where the leaves are removed.

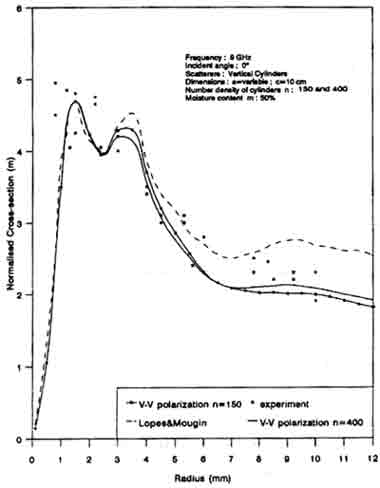
Fig 5 : Comparison between theory and measurements of normalised cross-section from a layer of vertical stems with different cylinder radii

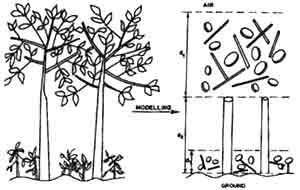
Fig 6(a) : Modelling of a forest canopy as a multilayer multiconstituent random medium

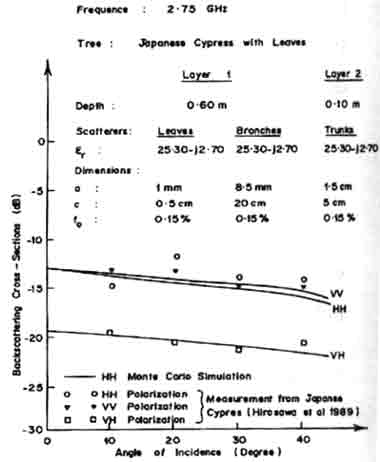
Fig 6(b) : Comparison of Monte Carlo calculations with measurements from Japanese Cypress trees (with leaves) at 2,75 GHz

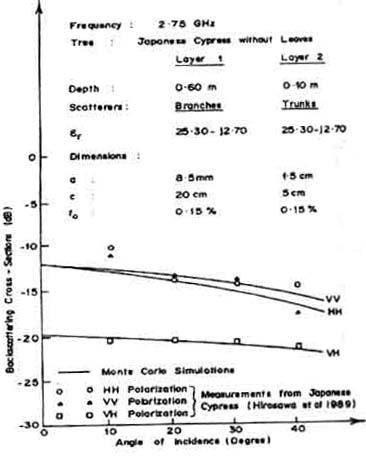
Fig 6(c) : Comparison of Monte Carlo calculations with measurements from Japanese Cypress trees (without leaves) at 2,75 GHz
5. Conclusions
This paper gives a review of some of the modeling work done in electromagnetic scattering and propagation in foliage and vegetation, as well as application examples in active remote sensing. The work is by no means complete. Many other issues should be researched into, such as a better formulation of phase matrix to describe vegetative component, the near-field effect of vegetative components which appear physically to be close to each other, and the overall structure and shape of a tree. These studies would shed light and to enhance our understanding of wave-mater interaction.

References

M.A. Karam, A.K. Fung, R.H. Lang and N.S. Chauhan, "A Microwave Scattering Model for Layered Vegetation", IEEE Trans. Geosci. Rem. Sens., vol. 30, no. 4, pp. 767-784, 1992.
H.T. Chuah and H.S. Tan, "A High Order Renormalization method for Radar Backscatter from a Random Medium", IEEE Trans. Geosci, Rem. Sens., Vol. 27, no. 1, pp. 79-85, 1989.
H.T. Chuah and H.S. Tan, "A Radiative Transfer Backscatter Model for a Vegetative layer of a Mixture of Discrete Scatterers", Journal of Electromagnetic Waves and Applications, vol. 4, no. 3, pp. 247-268, 19990.
H.T. Chuah and H.s. Tan, "A Radar Backscatter Model for A Forest Stand", Waves in Random Media, vol. 2, pp. 7-28, 1992.