GISdevelopment.net ---> AARS ---> ACRS 1998 ---> Digital Image Processing Incorporating Cluster Information into Multispectral Image Edge Detection Uthai Sangthongpraw, Yuttapong Rangsanseri, and Punya Thitimajshima Department of Telecommunications Engineeing, Faculty of Engineering King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand E-mail : kryuttha@kmitl.ac.th, ktpunya@kmitl.ac.th Abstract A multispectral image edge detection algorithm is proposed in this paper based on the idea that uses global spectral information to guide local gradient computation. The image is first segmented into a small number of cluster by using a clustering algorithm. Edges are then treated as transitions from one cluster to another. Edge detection is performed by calculating gradient magnitudes separately on each channel. The best linear projection which maximizes the inter-cluster distance will be used to recombine the gradient magnitudes in individual channels. The algorithm has been tested on JERS-1/OPS images, and the experimental results are included. 1. Introduction Edge detection plays very important roles in many image interpretation systems. For this reason, several edge detection algorithms have been proposed [1] [2]. JERS-1 satellite has optical sensor (OPS), which observes in seven spectral bands including three Visible and Near-Infrared (VNIR) bands. The interpretation of these VNIR images is usually done by associating the three bands with the three additive color primaries, RGB, in the display device. Edge detection in these images can be also performed by using general algorithms of the color image [3]. In some of many color edge detection algorithms, the RGB space is first transformed into other spaces in which the coordinates match the perceptual attributes of colors, e.g. HSI space, YC1C2 space. In these spaces, components are relatively independent to each other. Traditional edge detectors can be adopted in each channel and the results are recombined in ways that make use of both color and luminance information. In this paper, we present a method for edge detection in multispectral images by incorporating cluster information. In fact, edge pixels tend to occur in the boundary where the neighboring pixels belong to different cluster, Our method is studied for the case of three band images, thus usually referred as color images. 2. Two alternative approaches The monochrome version of a color image can be obtained by extracting the luminance component for each pixel. The linear combination of the R,G, and B components is usually used. Edge can be obtained by using the traditional edge detector. An alternative linearly for each pixel. 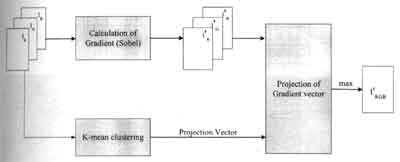The above two methods can be explained as : Figure 1: Block diagram of the proposed algorithm. I' = 0.31'r + 0.59I'g + 0.11I'b             (1) = (0.31'r + 0.59I'g + 0.11I'b)             (2) Where I'r, I'g, I'b and I'r, I'g, I'b denote the gradients and the intensities in each color channel respectively. We can see that this process can be viewed as the projection of multi-dimensional gradient vectors to scalar values [0.3, 0.59, 0.11], some gradient vectors with significant magnitudes can be projected to small values if the projection direction is not at the same direction of the gradient vectors. If several possible projection vectors are derived for a given multispectral JERS-1 image by statistic analysis, Then for each pixel, the gradient vector is projected in a way that results the maximum edge value. The spectral information can be used efficiently in this way. 3 The proposed method Clustering information is applied in this paper to find the appropriate projection vector. The information in every bands can be use efficiently in this algorithm. The block diagram of this method is shown in Figure 1. 3.1 Sobel operator Generally, the computation of gradient image is use Sobel operator [2]. The gradient is computed by convolution of input image and 3x3 dimentsion mask, denote Sx and Sy. The gradient in x and y directions are computed. The Sobel mask Sx and Sy are shown below. 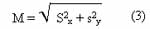Sx= -1 0 1 -2 0 2 -1 0 1   Sy= 1 2 1 0 0 0 -1 -2 -1 Figure 2: Sobel mask The gradient magnitude (M) can be calculated from the following equation : 3.2 Cluster analysis Each pixel in the image can be plotted as vector in a multidimensional space. The cluster analysis transforms the original remote sensing images into a set of linear chromatic. An appropriate chromatic transform is chosen for each pixel. In this paper, k-mean clustering method [4] is chosen. The algorithm is described in the following Allocate each pattern vector to a group corresponding to the nearest group mean. Calculate the new cluster centers as the average of all the pattern vectors in each cluster group. It they are al the same as the old cluster centers, STOP. Otherwise go to step 1. The cluster analysis provides the average vectors or the center (Ci, i = 1, 2 3, … , n) of each cluster and these vectors are used to calculate the appropriate projection vector. 3.3 Projection of gradient vectors Suppose two regions R1 and R2 belong to the cluster C1 and C2. The centers of these two clusters are V1 and V2. The gradient vector of a pixel around the boundary between R1 and R2 is likely to have the same direction of V1 -V2, Then V1 -V2 is a good choice of projection vector for edge between R1 and R2. For a given image, if n cluster are found, there are n(n-1)/2 possible projection vectors. If the standard projection vector, the number of possible projection vectors is then (n(n-1)/2+1. For each pixel of the image, its gradient vector is projected to all these (n(n-1)/2+1 projection vectors and the maximum value is adopted. 4. Experimental results In this paper, the proposed algorithm has been implemented and applied to several JERS-1/OPS-VNIR images, band 1,2 and 3. The gradient information in each spectral band is calculated using Sobel operator. The number of cluster allows for each image is 4. The original "color" JERS-1/OPS-VNIR image is shown in Figure 3(a). Figure 3(b) shows the segmented image resulting from the k-mean clustering algorithm. Figure 3(c) shows the gradient image calculated on the monochrome version of figure (3a). Comparing the Figure 3(d), which is the gradient image obtained by the proposed algorithm, it is obvious that more significant edges can be detected by this algorithm. (a) (b) (c) (d) Figure 3: Experimental result. (a) Original JERS-1/OPS-VNIR (color) image. (b) Segmented image of a (a) into 4 cluster. (c) Gradient image calculated on monochrome version of (a). (d) Gradient image obtained by the proposed method. 5. Conclusion The advantage of the proposed algorithm is that global information of a given multispectral remote sensing image is exploited to guide the local edge detector. Use of each spectral information is enabled by having multiple projection vectors. So this method can increase the efficiency of the edge detection, but some problems related this scheme is the computation complexity caused by the clustering process. This problem can be partially solved by sub-sampling the original image. Acknowledgement The authors wish to thank the national Research Council of Thailand (NRCT) for providing the satellite image data. Reference A.K. Jain, Fundamentals of Digital Image Processing. Prentice-Hall, Englewood Cliffs, 987. R.C. Gonzalez and R.E. Woods, Digital Image Processing, Addison -Westley, 1992. J.T. Allen and T. Hunsberger, "Comparing color Edge Dectection and Segmentation Methods, " In IEEE SOUTH EASTCON '89, pp. 722-758, 1989. A. Low; Introductory Computer vision and Image Processing. McGraw-Hill, 1991. R. Nevatia, "A color Edge Detecor and Its Use in Scene Segmentation, " IEEE Trans. Syst. Man Cybern., vol 7, pp. 820-826, 1997.