| GISdevelopment.net ---> AARS ---> ACRS 1998 ---> Digital Image Processing |
Multiresolution Fuzzy
Clustering For SAR Image Segmentation
Yuttapong Rangsanseri and
Punya Thitimajshima
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkraband, Bangkok 10520, Thailand
E-mail: Kryuttha@kmitl.ac.th, ktpunya@kmitl.ac.th
AbstractDepartment of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkraband, Bangkok 10520, Thailand
E-mail: Kryuttha@kmitl.ac.th, ktpunya@kmitl.ac.th
This paper describes a pyramid-based method for clustering single polarization synthetic Aperture Radar (SAR) images. A pyramid of the image is first constructed by using the wavelet transform. The fuzzy c-means (FCM) algorithm is then applied to the pyramid with the coarse-to-fine approach. Finally, clustering is followed by a majority filtering to obtain more homogeneous regions. The algorithm has been tested on JERS-1/SAR image and the results demonstrate its potential usefulness.
Introduction
The Japanese Earth Resources Satellite-1 (JERS-1) has provided synthetic Aperture Radar (SAR) image operative at 1.275 GHZ since its launch on Feb. 11, 1992. This radar remote sensing provides terrain image regardless of weather and operations time. The image itself is the result of microwave backscattering and is expected to provide different and important information on terrain, which cannot be obtained by any optical sensors.
Remote sensing image segmentation is often accomplished by clustering when ground truth is not available to provide samples to train a supervised classifier[1]. In this technique an image is segmented into unknown classes. It is the task of the user to label those classes afterwards. There are a great number of clustering methods. Many are accomplished by an iterative technique. An approach based on clustering a pyramid data structure has been proposed by Trivedi and Bezdek [2]. In that research, each layer in the pyramid is created by averaging groups of 2x2 pixels to produce a composite pixel of reduced resolution.
The segmentation of SAR images usually uses texture measures, describing the relation between gray levels of neighboring pixels, as feature for the classification algorithm feature, based on the multiresolution decomposition provided by the wavelt transform [3] [4]. The method also produces a pyramid structure similar to [2]. The image segmentation is performed by the multiresolution fuzzy clustering technique.
Multiresolution analysis
Multiresolution analysis [5] permits the analysis of the signal in different frequency bands or at different scales. In practice, mutiresolution analysis is carried out using 2 channel filter banks composed of a low-pass and a high-pass filter and each filter bank is then sampled at a half rate (1/2 down sampling) of the previous frequency.
Wavelet is type of filter family. They are constructed from a mother wavelet [6], which can be any admissible function. A family is constructed by dilating and translating the mother wavelet by different amount. In the case of an image, the filtering is implemented in a separable way by filtering the lines and columns. The low-pass filter of level I provides an approximation of the initial image at the scale of 2'. The high-pass filters give the image of the wavelet coefficients or the high frequency images.
Fuzzy clustering
The fuzzy clustering has been proved to be very well suited to deal with the imprecise nature of geographical information, including remote sensing data. According to the fuzzy clustering framework, each cluster is a fuzzy set, and each pixel in the image has a membership value associated to each cluster, ranging between 0 and 1, measuring how much the pixel belongs to that particular cluster. There have been many different families of fuzzy clustering algorithms proposed in the last decade [7]. The one used in this paper is the Fuzzy C-Means algorithm (FCM), which is an iterative technique based on the minimization of a generalized within group sum of squared (WGSS) err objective function.
The proposed algorithm
The proposed algorithm can be described by Figure 1. A multiresolution framework is exploited to reduce the computational burden while preserving good segmentation results. A pyramid of the image is obtained by using the wavelet transform. Each layer of the pyramid is consisted by 4 sub-images forming 4-dimension texture feature for the clustering. The FCM
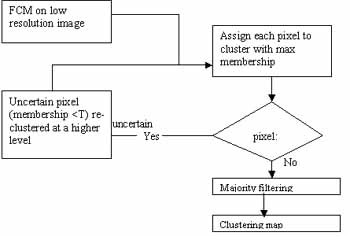
Figure 1: Overall scheme of the proposed algorithm
 (a) |
 (b) |
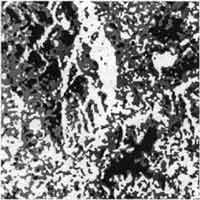 (c) Figue 2. Experimental results.(A) Original JERS-1/SAR image. (B) 2-level wavelet pyramid. (c) Final clustering map. | |
Algorithm is first implemented on the coarsest image approximation and a test a carried out, for each pixel, on the final membership value against a prescribed threshold T. The pixel is uncertain pixels at the finer image approximation. This procedure is iterated downward until the bottom of the pyramid is reached where all remaining uncertain pixels are labeled. Finally, the clustering is followed with a majority filtering to obtain more homogeneous regions. Since each time the algorithm operates on a very limited number of pixel, computation time is reduced by a large amount.
Results
Experiments were carried out for the proposed algorithm using different JERS-1/SAR image. An example is given in Figure 2. The original image consits of 1024 x 1024 pixels is show figure 2(a). the pyramid of this image computed by using 2-level wavelt multiresolution fuzzy clustering and majority filtering is given in Figure 2(c). Note that the majority filtered is perform within the window size of 3 x 3 pixels.
Conclusion
Amultiresolution fuzzy clustering approach to SAR image segmentation within a wavelet-based framework has been presented. It has been shows that wave let representation provides large computation time saving and useful feature to improves te result of the fuzzy clustering algorithm.
Acknowledgement
The authors with to thank the National Research Council of Thailand (NRCT) of providing the satellite image data.
Reference
- J.A. Richards, Remote Sensing Digital Image Analysis, Berlin: springer-Verlag, 1993.
- M.N. Trivedi and J.C. Bezdek, "Low-Level Segmenttion of Aerial Images with Fuzzy Clustering, "IEEE Transon Systems, man and Cybernetics, vol. SMC-16, no.4, pp.589-598,1986.
- C.S. Burrus, R.A. Gopinath, and H. Guo, Introduction to wavelets and Wavelet Transform, New Jersey: Perentice -hall International, Inc., 1998.
- S. Mallat, A Wavelet Tour of Signal Processing. San Diago: Academic Press, 1998.
- S. Mallant, "A Theory of Multiresolution Signal Decomposition: The Wavelet Representation," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 11, pp. 674-693, 1989.
- I. Daubechies, "Orthonormal Bases of Compaactly supported Wavelets," Comm. Pure and Applied Mathematics, vol. 41, no. 7, pp. 909-996, 1988.
- J.C. Bezek and S.K. Pal, Fuzzy Models for Pattern Recognition, IEEE Press 1992.