GISdevelopment.net ---> AARS ---> ACRS 1998 ---> Poster Session 3 Moving Average Method for Time Series Lidar Data Somkiat Lerkvarnyu, Kobchai Deijhan, Fusak Cheevasuvit Faculty of Engineering and Research Center for Communication and Information Technology, King Mongkut's Institute of Technology Ladkrabang, Ladkrabang Tel : 66-2-3269967, 66-2-3269081, Fax : 66-2-3269086 E-mail: kobcahi@telelan.telecom.eng.kmit.ac.th Abstract The processing of single wavelength aerosol lidar, this paper proposes the moving average method to attract the scattering ratio of sequence time series lidar data relating to the backscattering lidar signal. The information from normalized scattering ratio represents the aerosol locations with respect to altitude. The ground-based lidar system is classically obtained by comparing between measurement data and standard atmospheric model. The moving average method, does not need for the prior data, the parameter of empirical model will be estimated only from the time series data as the digitized lidar signal. Introduction The Rayleigh lidar, Mie lidar, Differential absorption lidar, Raman lidar and so on are the many types of faster radar or optical remote sensing to probe or study the characteristic of the atmosphere. All systems of laser radar use the various laser property to interact with particle concentration in the atmosphere such as absorption, scattering, depolarization and Doppler frequency shift. The appreciation to select the property for each type of lidar and in this paper concerned with the signal processing of ground-based Rayleigh lidar in which the technique will be used mainly the backscattering of the laser energy by whole particle in the atmosphere. Briefly, the Rayleigh lidar consist of Nd: YAG laser, transmitter that transmits the second harmonic wavelength (532 nm) and the laser beam is transmitted in the vertical axis with respect to the earth. The receiver uses the telescope with 28 cm diameter that will collect the scattered laser light from molecule and any particle in the field of view of receiving telescope. The collected light by telescope will focus on a photomultiplier which converts the energy to be electrical signal. The reflected signal will be changed from analog to digital (A/D) by LeCroy 9310. Finally, the digital signal will be transferred to a personal computer where the signal will be processed and analyzed via parallel port. There are many methods to analysis lidar signal depending on the investigation. Normally, the reflected signal was obtained by scattered the whole particle in the laser beam so that it can separate into two classes. One is the deterministic signal occurring from the backscattering of laser light only by mixture of gases with homogeneous assumption. Moreover, for the short period the mixture of gases can be considered as time-invariance process. The characteristic of deterministic signal will decrease with altitude that corresponds to the density number of the average gases or decrease as linear trend in the log scale so that it can look as the time series of linear trend process. Another is the random signal that obtain from the backscattering of laser light by aerosol, thin cloud or any particle that moving, which be called speckle, or may be stationary in the atmospheric. Normally, the random signal meaning is the information to indicate the location of aerosol which determines from the scattering in the classical method. It has several methods to process the time series lidar signal and the main purpose is filter or smoother, the signal model and he residual signal analysis that will be discuss. Moving average filter for the time series The time series lidar data that close to the digital signal with speckle or noise can be improved by various methods such signal average or some method of filter. In moving average method it considers as the mean of statistical data which can be written as follows; t=u+et   (1) {et} are uncorrelated random variable with zero mean and variance se and us is unknown parameter which is different depending on the wide of data sequence. 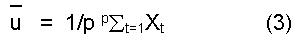Suppose that whole observations from the origin of time through the current point, x1,x2,...xp, are available, the minimum of u can be obtained from lest-square criterion, thus L(u) = PSt=1 (xt-u)2   (2) For the condition dL/du = 0, ten the equation can be rewritten that is the characteristics of arithmetic mean, or sample mean, at the p data point from observation. The arithmetic mean collect al past data point until point p so that. 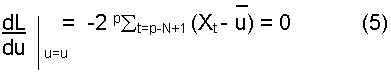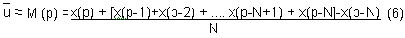Consider the time series N points, it can be written as L (u) = PSt=P-N+1 (xt-u)2   (4) For the data N points and and the estimated parameter is or M(p)=M(p-1) + (x(p)-x(p-))/N    (7) M(p) normally was called an p-period simple average and N is called the span of moving average. Moreover, it is possible to obtain M (p) directly from previous value, the behavior of simple moving average method looked as low-pass filter and its property depend on the span, for the span N is large, the moving average will be slowly to change in the parameter u, and will be rapidly as the span is small. Lidar signal processing The signal processing of lidar time series will be separated into two topics. First, with the moving average method, to determine the model of the signal that obtains from the backscattering by whole particle. Another is the estimated parameter of the deterministic model by regression method. The characteristic of time series lidar data will decrease with altitude or decrease as linear trend in the log scale so hat it can be looked as the time series of linear trend process as described Xt = u1 + u2t + et   (8) u1 and u2 are unknown parameters that will be estimated from the data sequence and {et} are uncorrelated random variable with zero mean and variable se=. From the previous topic, M(p) is the p-period simple moving average. The expected value of M(p) for linear trend is; E[M(p)] = (E[x(p) + x(p-1) + x (p-2) + .... x (p-N+1)])/N    (9) = 1/N [ u1 + u2p + u1+ u2 (p-1) + .... u1 + u2 (p-N+1)] = u1 + u2p - (N-1)u2/2 E[M(p) = E[x(p)] - (N-1)u2/2    (10) Consider the moving average of the moving average, it can be written as 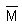= Moving average of the moving average 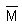= M(p) + [M(p-1) + M (p-2) + ………….. 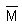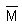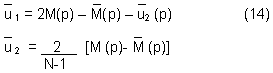+ M(p-N+1) +M (p-N)]-M(p-N)    (11) N or = M(p-1) + (M(p)- M(p-n))/N    (12) Usually, it is so called the moving average of moving average is double moving average, and the expected value of double moving average is; E[] = E[x(p) - (N-1)u2    (13) = u1 + u2p - (N-1)u2 the estimated parameter u1, u2 will be obtained by solving equation (10) and (13) So that the observation estimation in period p should be 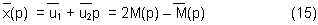The parameter estimation of deterministic signal can be calculated by least-square fitting. Moreover, the interval time series will be used to estimate parameters and it is important. The period of time series corresponding to altitude in which it has many aerosol or thin cloud and it can be selected and the estimated parameter is not correct. Normally, the altitude will be selected for parameter estimation of deterministic signal is 20 km height at which it has no aerosol assumption. 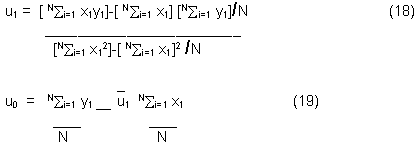The written model in term of observation is; y1 = u0 + u1x1 + ei       i = 1,2, ......, N     (16) The least-square function is L(u0,u1) = NSi=1(yi-u0-u1xi)2    (17) The estimated parameter can be obtained from Having estimated the parameter of moving average and parameter of deterministic signal, the information of lidar time series data can be obtained by the difference or ratio form its model. Summary Signal processing by moving average method for estimation and model fitting of time series lidar data have been describe in this paper. This method depends on the N points of data that effect the estimated parameter. Because the moving average process uses all past of N-point data, the random data can be processed for empirical model fitting. The information of time series lidar data are obtained by the difference of ratio between deterministic and random signal. However, for more accuracy the deterministic signal can be obtained from the standard atmospheric model or radiosonde. References D. R. Brillinger, Time series data analysis and theory, McGraw-Hill, U. S. A., 1981. B. Porat, Digital processing of random signal: theory and method, Pretice Hall, Englewood Cliffs, 1994 G. M. Jenkins and D. G. Watt, Spectral analysis and it applications, Holden-Day, 1968. R. M. Measures, Laser Remote Sensing: Fundamentals and Application. New York, NY: Wiley, 1984. P. B. Russell and B. M. Morley, J. Appl. Opt., vol. 21, pp. 1554-1563, 1962.