| GISdevelopment.net ---> AARS ---> ACRS 1999 ---> Hyper Spectral Image Processing |
Adaptable Class Data
Representation for Hyperspectral Image Classification
Xiuping Jia
School of Electrical Engineering, University College
The University of New South Wales
Australian Defence Force Academy
Campbell, ACT 2600 Australia
Tel: (61)-2-6268-8202 Fax: (61)-2-6268-8443
Email: tseng@mail.ncku.edu.tw
School of Electrical Engineering, University College
The University of New South Wales
Australian Defence Force Academy
Campbell, ACT 2600 Australia
Tel: (61)-2-6268-8202 Fax: (61)-2-6268-8443
Email: tseng@mail.ncku.edu.tw
Keywords: Hyperspectral, Classification,
Clustering, Data Representation, Histograms.
Abstract
This paper presents a procedure on how to establish an adaptable class data representation instead of adopting the Gaussian distribution assumption. By combining supervised and unsupervised classification methodologies, the data is represented in a one-dimensional cluster-space and a set of subclass signatures is generated to fit class data better. This results in a better performance than the conventional minimum distance classification technique. Since only the first degree of statistics is used in the proposed method, the number of training samples required can be much fewer than that for using maximum likelihood classification. Experiments have been carried out using an AVIRIS data set and the advantages in nonparametric multi-signature classification are demonstrated with improved classification accuracy.
1. Introduction
Hyperspectral remote sensing data, such as recorded by AVIRIS, covers the full solar reflected portion of the spectrum with high spectral resolution of 10 nm. It provides rich information on ground cover types and makes possible detailed study and monitoring of the Earth. However, data representation and interpretation become difficult due to the high dimensionality which is the result of using hundreds of spectral bands.
Statistical maximum likelihood classification is based on the assumption that the probability distribution for each class is of the form of a multivariate normal model with dimensions which equal the number of spectral bands. This parametric method has been widely used for broad-band remote sensing data, for example, Landsat MSS and TM data. However it requires a large number of training samples for each class in order to obtain reliable estimation of statistics. The rule of thumb is that the number of training pixels per class should be at least 10 times the number of bands used, and desirably 100 times (Swain and Davis, 1978). However, the number of training pixels is always limited in remote sensing image classification, since training pixel identification is a time-consuming step and can be very costly. When the number of training samples is finite, maximum likelihood classification accuracy will not always increase with the number of features used; it starts to decrease when the ratio of the number of training samples to the dimensionality is low. This has been referred to as the Hughes phenomenon (Hughes, 1968). Therefore, the reliability of maximum likelihood classification is reduced for hyperspectral data.
Neural network methods have been used in hyperspectral remote sensing data classification in the recent years due to their nonparametric properties (Benediktsson et al., 1993). Particularly, multiple Kohonen self-organizing maps have been proposed which represent data’s high-order statistics using several model-free elastic ‘maps’ (Wan and Fraser, 1999). Among the parametric methods, the minimum distance classifier is more effective than the maximum likelihood classifiers when training data is limited since it needs only to estimate the class mean position. However, an information class is often not sufficiently represented by its mean position and is expected to consist of a set of spectral classes, ie. clusters. To allocate the associated clusters to an information class, a hybrid supervised and unsupervised methodology has been developed. Unsupervised clustering is performed first, the clusters are then recognized as information classes with the aid of the inspection of the bispectral plots of the spectral class centres and the training data (Jia and Richards, 1999). This procedure can be reasonably implemented manually for a conventional low dimensional data. With hyperspectral data, however, it will be a difficult task to identify subclasses manually since visualization of the reference data and cluster centres are impossible. An automatic supervised nonparametric classifier was proposed by Skidmore and Turner (1988) and tested with SPOT data. For each class, training data is used to construct a feature-space histogram, that is, the plot of the number of training pixels for each feature space cell. The cell is assigned to the class whose normalized histogram count is the highest. A LUT is then created for labeling unknown data. This classifier treats each cell as a separate decision rule and the real class data distribution shape is used. Therefore the classification accuracy can be improved. However, the number of cells will be too high and the histograms will be very sparse and flat for hyperspectral data.
In this paper, the hybrid classification method has been extended and further developed quantitatively. Cluster-space data representation is proposed so that a set of cluster mean signatures is generated for each class automatically. The method can be implemented easily regardless of the number of spectral bands used. Experimental results have shown that the new method can improve the classification accuracy.
2. Methods
2.1 Cluster-Space Data Representation
Since an information class data set is often not sufficiently represented by its mean position only, it is expected to be represented by a set of spectral classes, ie. clusters. These clusters however must be separable from other classes’ clusters. Therefore, the separable clusters are first generated from all the training data. Clustering algorithms, for example, ISODATA (K-means) (Schowengerdt, 1997), can be employed in this step. To ensure adequate data representation, a large number of clusters are generated. The cluster vectors will be used to replace the original radiometric ranges, say 12 bits. The original training data is then labeled into the clusters generated based on Euclidean distance measure. For each class, the number of pixels which are labeled into each cluster will be counted and a histogram can be plotted. The graph provides a cluster-space representation of the training data. A summary is given below.
Let x be a pixel vector of length N which is the number of the spectral bands used. There are Li training pixels for class wi. They are
xi,1, xi,2, . . .xi,L.
The new representation of these data is
hi(1), hi(2), ...hi(K).
where K is the number of clusters which are generated from all the training data. hi(k) is the number of samples from class wi which are labeled as cluster k. Obviously,
hi(1)+hi(2)+ . .
.hi(K)=Li .
The advantage of the new representation is that the high dimensional data has been displayed in a one-dimensional cluster-space. Class data examination becomes easier with the available histogram plots. The histograms also show how the class data is distributed among the clusters. To account for the different training set sizes in each class, normalized histograms are used, which can be found by
Hi(k)=(hi(k)/Li)
x100%, k=1,2,. . .K
Hi(k) indicates the chance of finding a pixel of class wi from the cluster k. In other words, this is the estimated probability distribution for class wi. Instead of adopting the common assumption of Gaussian distribution, the cluster-space data representation makes the use of the true distribution shape possible in the classification process. This is discussed in the following section.
2.2 Cluster Assignments Using Bayes’ Rule
After each class training data has been represented by the given set of clusters, clusters can be recognized as an associated spectral classes of information classes.
The cluster vector is identified by its index number k, k= 1,2,3, . . .K. Hi(k), k=1,2,3, . . .K represents the probability distribution for class wi in the cluster-space. Hi(k), i=1,2,3, . . .M gives the relative likelihoods that the cluster vector k belongs to each defined class. Cluster index k can be classified into the information classes using Bayes’ Theorem. Assuming that prior probabilities are equal for all the classes, the decision rule is:
kÎ
wi, if
Hi(k)>Hj(k) for all
j>¹i (1)
This cluster assignment process is simple, fast and reliable (assume that the training data is reliable) for the following reasons: (i) This is a one dimensional problem; (ii) The number of data to classify (K) is small; (iii) The true probability distribution shapes are used.
The clusters labels, wi, are stored for later use in classifying unknown data. If the probability values Hi(k) are recorded as well, it will be possible to provide information on how reliable the classification results are.
Since several clusters may be labeled as the same class generally, each class has been defined by a group of clusters. In other words, instead of using a single mean position as a class signature, several cluster mean positions are used. This multi-signature structure generates a flexible and adaptable representation which is wholly determined by the training data itself.
2.3 Unknown Data Classification
There are two steps in labeling an unknown pixel vector.
An unknown pixelvector x will be first classified into one of the given set of clusters (k) using the minimum distance classifier. The dicision rule is:
xÎk, ifd(x,
ck)2<d(x,cj)2
for all k¹j (2)
where ck is the mean vector of the cluster k data and d(x, ck)2=(x –ck)t (x –ck).
The second step is to label the data into the classes with which the cluster is associated.
xÎ wi,
if kÎ wi. (3)
3. Experiments
An AVIRIS data set covering an area of mixed agriculture and forestry in Northwestern Indiana, USA, was used in the following tests. It was recorded in June, 1992 with 220 bands. Water absorption bands, 104 to 108 and 150 to 162, were removed, leaving 202 bands. A traditional principal components transformation was applied to the data and the first 40 new features, which contained 99.93% of total variance in the original data, were used for the tests. 4 classes were selected as shown in Fig.1.

Fig. 1. The Image and the Reference Data.
The ISODATA clustering algorithm was run using the software package MultiSpec (Landgrebe and Biehl, 1999). 20 clusters were generated from the training data for the four classes. The training samples were then labeled into the defined clusters. The results have been normalised to show the percentage (density) of the training pixels which were labeled into each of the clusters. They are plotted in Fig. 2.
It can be seen from Fig. 2 that three clusters, Clusters 2, 4 and 6, were shared with more than one class. The rest of clusters has been fully dominated by one class only, ie., Hj(k)=0 for j.i. Nevertheless, all the 20 clusters have been assigned to one of the 4 classes, using the decision rule given in (1). The allocation results for all the clusters are given in Table 1.
Each class has been represented by several clusters. The cluster vectors form the multiple signatures for each class.
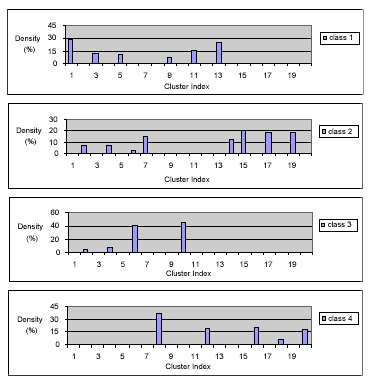
Fig. 2. The Cluster-Space Training Data Representation.
Table 1. The Subclasses of the Information Classes
To assess the algorithm quantitatively, the training data and the testing data have been classified using the two-step decision rules given in (2) and (3) and the conventional minimum distance classifier (single signature) for comparison purposes. Table 2 shows the classification accuracy obtained from the two methods. The classification results on the training data and the testing data have both been improved significantly.
Table 2. Overall Classification Results
Comparison
4. Discussion and Conclusion
Cluster-space data representation plays an important role in data analysis, especially for hyperspectral data. Firstly, class distributions (spreadness) can be easily inspected. More importantly, the separability between the classes can be examined and quantified. For example, 6.7% and 5.4% of the training pixels from class 2, ‘Corn’, and class 3, ‘Grass’, are classified into Cluster 2 (none from the rest of classes). While Cluster 2 will be assigned to class 2, those samples can be selected for detailed examination in order to find out the physical reasons for overlapping. There may be some bad samples which should be deleted from the reference data. Secondly, the probability (density) values, Hi(k), provides extra information on how reliable the classification results are. For example, if an unknown pixel is labeled as Cluster 2 and therefore classified as ‘corn’, the assignment is not very reliable since Cluster 2’s probability value is only 6.7%.
To reduce the number of overlapping clusters, the total number of clusters to generate needs to be sufficiently high. However, the selection of the number of clusters to use requires experience or trial and error. If a large number of clusters is used, it will increase the computational load.
The shapes of the density plots as shown in Fig. 2 are less important, since whatever the shape, it will be represented directly by the discrete density values. If a shape which is closed to a normal distribution is preferred for better presentation, it can be achieved by reordering the cluster index, assuming the class data is reasonably separable.
The proposed classification method provides a means to represent data which are distributed other than normally. The multiple signatures formed from the associated clusters are adaptable to the individual class distribution shape. On the basis of experiments conducted so far, classification accuracy will be higher than that using minimum distance classification. While the method is not as robust as the maximum likelihood method in terms of coping with the noise in the data, the requirement for the training data size can normally be met more easily for hyperspectral data.
5. Acknowledgement
The work presented in this paper was done in part when the author was a Visiting Fellow in the Department of Forestry, The Australian National University and the author thanks Dr. B. Turner for his helpful discussions during that time. The author also thanks Dr. D. Landgrebe of the School of Electrical and Computer Engineering, Purdue University, for providing the AVIRIS data set and the MultiSpec software package.
6. Reference
Abstract
This paper presents a procedure on how to establish an adaptable class data representation instead of adopting the Gaussian distribution assumption. By combining supervised and unsupervised classification methodologies, the data is represented in a one-dimensional cluster-space and a set of subclass signatures is generated to fit class data better. This results in a better performance than the conventional minimum distance classification technique. Since only the first degree of statistics is used in the proposed method, the number of training samples required can be much fewer than that for using maximum likelihood classification. Experiments have been carried out using an AVIRIS data set and the advantages in nonparametric multi-signature classification are demonstrated with improved classification accuracy.
1. Introduction
Hyperspectral remote sensing data, such as recorded by AVIRIS, covers the full solar reflected portion of the spectrum with high spectral resolution of 10 nm. It provides rich information on ground cover types and makes possible detailed study and monitoring of the Earth. However, data representation and interpretation become difficult due to the high dimensionality which is the result of using hundreds of spectral bands.
Statistical maximum likelihood classification is based on the assumption that the probability distribution for each class is of the form of a multivariate normal model with dimensions which equal the number of spectral bands. This parametric method has been widely used for broad-band remote sensing data, for example, Landsat MSS and TM data. However it requires a large number of training samples for each class in order to obtain reliable estimation of statistics. The rule of thumb is that the number of training pixels per class should be at least 10 times the number of bands used, and desirably 100 times (Swain and Davis, 1978). However, the number of training pixels is always limited in remote sensing image classification, since training pixel identification is a time-consuming step and can be very costly. When the number of training samples is finite, maximum likelihood classification accuracy will not always increase with the number of features used; it starts to decrease when the ratio of the number of training samples to the dimensionality is low. This has been referred to as the Hughes phenomenon (Hughes, 1968). Therefore, the reliability of maximum likelihood classification is reduced for hyperspectral data.
Neural network methods have been used in hyperspectral remote sensing data classification in the recent years due to their nonparametric properties (Benediktsson et al., 1993). Particularly, multiple Kohonen self-organizing maps have been proposed which represent data’s high-order statistics using several model-free elastic ‘maps’ (Wan and Fraser, 1999). Among the parametric methods, the minimum distance classifier is more effective than the maximum likelihood classifiers when training data is limited since it needs only to estimate the class mean position. However, an information class is often not sufficiently represented by its mean position and is expected to consist of a set of spectral classes, ie. clusters. To allocate the associated clusters to an information class, a hybrid supervised and unsupervised methodology has been developed. Unsupervised clustering is performed first, the clusters are then recognized as information classes with the aid of the inspection of the bispectral plots of the spectral class centres and the training data (Jia and Richards, 1999). This procedure can be reasonably implemented manually for a conventional low dimensional data. With hyperspectral data, however, it will be a difficult task to identify subclasses manually since visualization of the reference data and cluster centres are impossible. An automatic supervised nonparametric classifier was proposed by Skidmore and Turner (1988) and tested with SPOT data. For each class, training data is used to construct a feature-space histogram, that is, the plot of the number of training pixels for each feature space cell. The cell is assigned to the class whose normalized histogram count is the highest. A LUT is then created for labeling unknown data. This classifier treats each cell as a separate decision rule and the real class data distribution shape is used. Therefore the classification accuracy can be improved. However, the number of cells will be too high and the histograms will be very sparse and flat for hyperspectral data.
In this paper, the hybrid classification method has been extended and further developed quantitatively. Cluster-space data representation is proposed so that a set of cluster mean signatures is generated for each class automatically. The method can be implemented easily regardless of the number of spectral bands used. Experimental results have shown that the new method can improve the classification accuracy.
2. Methods
2.1 Cluster-Space Data Representation
Since an information class data set is often not sufficiently represented by its mean position only, it is expected to be represented by a set of spectral classes, ie. clusters. These clusters however must be separable from other classes’ clusters. Therefore, the separable clusters are first generated from all the training data. Clustering algorithms, for example, ISODATA (K-means) (Schowengerdt, 1997), can be employed in this step. To ensure adequate data representation, a large number of clusters are generated. The cluster vectors will be used to replace the original radiometric ranges, say 12 bits. The original training data is then labeled into the clusters generated based on Euclidean distance measure. For each class, the number of pixels which are labeled into each cluster will be counted and a histogram can be plotted. The graph provides a cluster-space representation of the training data. A summary is given below.
Let x be a pixel vector of length N which is the number of the spectral bands used. There are Li training pixels for class wi. They are
The new representation of these data is
where K is the number of clusters which are generated from all the training data. hi(k) is the number of samples from class wi which are labeled as cluster k. Obviously,
The advantage of the new representation is that the high dimensional data has been displayed in a one-dimensional cluster-space. Class data examination becomes easier with the available histogram plots. The histograms also show how the class data is distributed among the clusters. To account for the different training set sizes in each class, normalized histograms are used, which can be found by
Hi(k) indicates the chance of finding a pixel of class wi from the cluster k. In other words, this is the estimated probability distribution for class wi. Instead of adopting the common assumption of Gaussian distribution, the cluster-space data representation makes the use of the true distribution shape possible in the classification process. This is discussed in the following section.
2.2 Cluster Assignments Using Bayes’ Rule
After each class training data has been represented by the given set of clusters, clusters can be recognized as an associated spectral classes of information classes.
The cluster vector is identified by its index number k, k= 1,2,3, . . .K. Hi(k), k=1,2,3, . . .K represents the probability distribution for class wi in the cluster-space. Hi(k), i=1,2,3, . . .M gives the relative likelihoods that the cluster vector k belongs to each defined class. Cluster index k can be classified into the information classes using Bayes’ Theorem. Assuming that prior probabilities are equal for all the classes, the decision rule is:
This cluster assignment process is simple, fast and reliable (assume that the training data is reliable) for the following reasons: (i) This is a one dimensional problem; (ii) The number of data to classify (K) is small; (iii) The true probability distribution shapes are used.
The clusters labels, wi, are stored for later use in classifying unknown data. If the probability values Hi(k) are recorded as well, it will be possible to provide information on how reliable the classification results are.
Since several clusters may be labeled as the same class generally, each class has been defined by a group of clusters. In other words, instead of using a single mean position as a class signature, several cluster mean positions are used. This multi-signature structure generates a flexible and adaptable representation which is wholly determined by the training data itself.
2.3 Unknown Data Classification
There are two steps in labeling an unknown pixel vector.
An unknown pixelvector x will be first classified into one of the given set of clusters (k) using the minimum distance classifier. The dicision rule is:
where ck is the mean vector of the cluster k data and d(x, ck)2=(x –ck)t (x –ck).
The second step is to label the data into the classes with which the cluster is associated.
3. Experiments
An AVIRIS data set covering an area of mixed agriculture and forestry in Northwestern Indiana, USA, was used in the following tests. It was recorded in June, 1992 with 220 bands. Water absorption bands, 104 to 108 and 150 to 162, were removed, leaving 202 bands. A traditional principal components transformation was applied to the data and the first 40 new features, which contained 99.93% of total variance in the original data, were used for the tests. 4 classes were selected as shown in Fig.1.

| Class Name | Training Fields | No. of Training Pixels | Testing Fields | No. of Testing Pixels |
| Soybean | 1, 2 | 121 | 3 | 156 |
| Corn | 4 | 105 | 5, 6 | 75 |
| Grass | 7 | 56 | 8 | 60 |
| Hay | 9 | 95 | 10 | 96 |
Fig. 1. The Image and the Reference Data.
The ISODATA clustering algorithm was run using the software package MultiSpec (Landgrebe and Biehl, 1999). 20 clusters were generated from the training data for the four classes. The training samples were then labeled into the defined clusters. The results have been normalised to show the percentage (density) of the training pixels which were labeled into each of the clusters. They are plotted in Fig. 2.
It can be seen from Fig. 2 that three clusters, Clusters 2, 4 and 6, were shared with more than one class. The rest of clusters has been fully dominated by one class only, ie., Hj(k)=0 for j.i. Nevertheless, all the 20 clusters have been assigned to one of the 4 classes, using the decision rule given in (1). The allocation results for all the clusters are given in Table 1.
Each class has been represented by several clusters. The cluster vectors form the multiple signatures for each class.

Fig. 2. The Cluster-Space Training Data Representation.
Table 1. The Subclasses of the Information Classes
| Soybeans | Corn | Grass | Hay | |
| Clusters (Subclasses) | 1,3,5,9,11,13 | 2,7,14,15,17,19 | 4,6,10 | 8,12,16,18,20 |
To assess the algorithm quantitatively, the training data and the testing data have been classified using the two-step decision rules given in (2) and (3) and the conventional minimum distance classifier (single signature) for comparison purposes. Table 2 shows the classification accuracy obtained from the two methods. The classification results on the training data and the testing data have both been improved significantly.
| Training Data | Testing Data | |
| Conventional Single Signature | 78% | 59% |
| Multi-Signature | 97% | 74% |
4. Discussion and Conclusion
Cluster-space data representation plays an important role in data analysis, especially for hyperspectral data. Firstly, class distributions (spreadness) can be easily inspected. More importantly, the separability between the classes can be examined and quantified. For example, 6.7% and 5.4% of the training pixels from class 2, ‘Corn’, and class 3, ‘Grass’, are classified into Cluster 2 (none from the rest of classes). While Cluster 2 will be assigned to class 2, those samples can be selected for detailed examination in order to find out the physical reasons for overlapping. There may be some bad samples which should be deleted from the reference data. Secondly, the probability (density) values, Hi(k), provides extra information on how reliable the classification results are. For example, if an unknown pixel is labeled as Cluster 2 and therefore classified as ‘corn’, the assignment is not very reliable since Cluster 2’s probability value is only 6.7%.
To reduce the number of overlapping clusters, the total number of clusters to generate needs to be sufficiently high. However, the selection of the number of clusters to use requires experience or trial and error. If a large number of clusters is used, it will increase the computational load.
The shapes of the density plots as shown in Fig. 2 are less important, since whatever the shape, it will be represented directly by the discrete density values. If a shape which is closed to a normal distribution is preferred for better presentation, it can be achieved by reordering the cluster index, assuming the class data is reasonably separable.
The proposed classification method provides a means to represent data which are distributed other than normally. The multiple signatures formed from the associated clusters are adaptable to the individual class distribution shape. On the basis of experiments conducted so far, classification accuracy will be higher than that using minimum distance classification. While the method is not as robust as the maximum likelihood method in terms of coping with the noise in the data, the requirement for the training data size can normally be met more easily for hyperspectral data.
5. Acknowledgement
The work presented in this paper was done in part when the author was a Visiting Fellow in the Department of Forestry, The Australian National University and the author thanks Dr. B. Turner for his helpful discussions during that time. The author also thanks Dr. D. Landgrebe of the School of Electrical and Computer Engineering, Purdue University, for providing the AVIRIS data set and the MultiSpec software package.
6. Reference
- Benediktsson, J.A., Swain, P.H. and Ersoy, O.K., 1993. Conjugate-gradient neural networks in classification of multisource and very-high-dimensional remote sensing data. Int. J. Remote Sensing, 14(15), pp. 2883-2903.
- Hughes, G. F., 1968. On the mean accuracy of statistical pattern recognizers. IEEE Transactions on Information Theory, IT-14 (1), pp. 55 - 63.
- Richards, J.A. and Jia, X., 1999. Remote Sensing Digital Image Analysis. 3 rd Ed. Springer-Verlag, Berlin.
- Landgrebe, D.A. and Biehl, L., 1999. An introduction to MultiSpec. West Lafayette, IN, Purdue Univ. Press.
- Schowengerdt, R.A., 1997. Remote Sensing Models and Methods for Image Processing. Academic Press, San Diego.
- Skidmore A.K. and Turner, B.J., 1988. Forest mapping accuracies are improved using a supervised nonparametric classifier with SPOT data. Photogrammetric Engineering and Remote Sensing, 54 (10), pp. 1415-1421.
- Swain, P.H. and Davis, S.M. (eds), 1978. Remote Sensing: The Quantitative Approach. McGraw-Hill, New York.
- Wan, W. and Fraser, D., 1994. Multiple Kohonen SOMs: Supervised and unsupervised formation. Proc. ACNN’94, Brisbane, Australia, pp. 17-20.