Research on the displacement of Spot Images

Research on the displacement of Spot Images

Zhang Yonghong, Zheng Jixen, Lin Zongjian
Chinese Academy of Surveying and Mapping
Beijing, 100039, P.R. China

Abstract
Displacement of SPOT images with vertical and titled viewing angle arising form topographic relief is investigated in detail , corresponding formulae are deduced, and the displacement value of SPOT image naturalized to 1:5000 scale resulted from relief is listed. The usually used rectification methods, polynomial rectification and digital differential rectification, are introduced in the genera , a new correction method without DEM is proposed, which can be used to rectify the SPOT images in large relief region, an experiment on this method is accomplished.

SPOT images are widely applied to topography mapping, land use/land cover mapping and change detection, forests resource management, city planning etc, so geometrical rectification of SPOT image is very important. The essence of rectification is to project images to a desired plane and keep the point displacement within the limited range so as to make the image be a image nap with precise planimetric coordinate. The usually used rectification methods of SPOT images include polynomial rectification and differential rectification, differential rectification is more precise and more computationally expensive. Selecting which rectification method depends on the ground relief, image viewing angle and application need. So to determine the displacement of SPOT image with different viewing angle arising from topographic relief is significant. This issue will be investigated in detail , and be presented in mathematical formulate. Under the conditions of no DEM, a new rectification method of SPOT images in large relief region is developed.

SPOT image Point Displacement
Image point displacement is the difference of image point in practices status and the image point in idealization status, so -called idealization is the status that ground surface is absolutely flat and photograph plane is parallel t ground surface. The nadir-on image in idealization status is orthoimage itself.

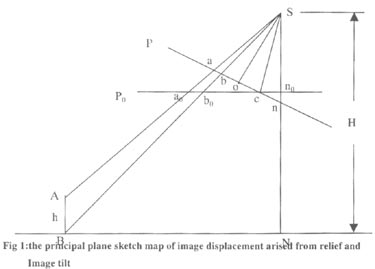
Every SPOT scan line is center projection image, with different exterior elements in different line. Usually, image point displacement arises out ot tilt angle of photo plane and topographic relief, for SPOT images, we think images point displacement is mainly attributed to topographic relief. In the following, images point displacement due to topographic relief in titled photograph will be discussed in detail.

In fig . 1, S is the photographic center, P is titled photograph, P_o is the corresponding horizontal photograph, c is the iso center of photograph , A is a ground point with elevation h, B is the projective Point of A in level surface, Sn₀=So= principal distance f, image plane coordinate system is set up with its origin c and isometic parallel, principal line as x axes, y axes respectively, A and B are respectively projected to a and b in photograph P, a₀ and b₀ in photograph P₀ ab correspond the images point displacement due to topography undulation, and is denoted by d_h, from the relevant knowledge of [1], the coordinate ( x,y) of point b in tilted photograph P with its origin o and the coordinate ( x_t, y_t ) of point b₀ in horizontal photograph P₀ with its origin n₀ has the relationship:

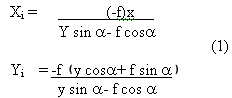
Where a is the tlt angle of photograph P.
If the tilted photograph origin is translated to photo nadir point n, and the coordinate of b is expressed as ( x_n, y_n), then x= x_n, Y_n= y+f tg a , Eqs ( 1) can be written as :

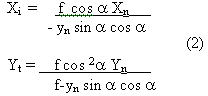
In ground surface, we set up the coordinate system with N as its origin and axes parallel to the axes of photograph plane, the coordinate ( X_n, Y_n) of point B and the coordinates ( X_t Y_t) of point b_o has the relationship : X_t = f X_n / H , Y_t = f Y_n / H, then :

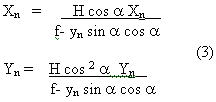
the length of vector nb is r_b = Ö x²_n + Y²_n, where Y_n= r_b sin F, F is the argument of vector nb , The length of vector Nb can be written as :

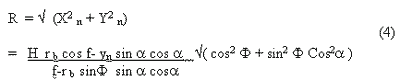
similarly, if we keep other condition unchanged except that we let the A point as the zero height point, a is the corresponding image point of A, r_a is the length of vector na , then R can be expressed as :

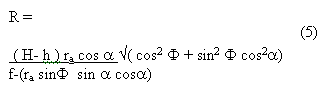
we can obtain the image point displacement d_h from Eqs. (4) and (5).

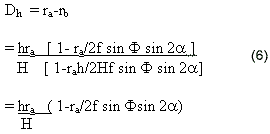
This is the algorithm for determining the image point displacement in oblique photograph with tilt angle a due to topography undulation h, but we must pay attention that r_a denotes the length of vector with its origin at photo nadir point.

As to SPOT images, because the filt of photo is not considered , then ( 6) can be written as :

Where, r denotes the distance between image point and image center line, ? is the incidence angle. We differentiate Eqs. (7) to h and ? respectively, the results are :

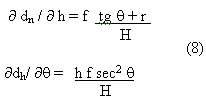
From Eqs. (8) we can conclude that photograph incidence has larger impact on image point displacement than topography undulation, in other words, photographs incidence magnifies the image point displacement from topography undulation, the following table 1 also support this conclusion.

The flight height of SPOT satellite is 822 km, pixel size in image is 13 mm , the photographic scale of PA image and XS image is respectively 1:8000, 000 and 1:400,000, the algorithm to determine displacement Dh in rectified scale form displacement dh in image is :

Dh= d_h (m/M) , where m is photographic scale and M is the rectified scale.

For SPOT PA images, ignoring the tilt of photograph, we naturalize the maximum point displacement in image with different incidence angle resulted from topograph undulation to 1:50000 rectified scale, the result is listed in table 1:

Table 1 maximum displacement of SPOT image naturalized to 1:50000 scale due to topographic relief

(unit :mm)

Underation (m)	Incidence angle ( degree)
Underation (m)	0	0.6	1.2	1.8	2.4	3.6	6	9	12	15	27
100	0.07	0.09	0.11	0.13	0.16	0.20	0.28	0.39	0.50	0.61	1.09
200	0.14	0.19	0.23	0.27	0.31	0.40	0.56	0.78	0.99	1.22	2.18
300	0.22	0.28	0.34	0.40	0.47	0.59	0.85	1.17	1.49	1.82	3.27
400	0.29	0.37	0.46	0.54	0.62	0.79	1.13	1.56	1.99	2.43	4.36
500	0.36	0.47	0.57	0.67	0.78	0.99	1.41	1.94	2.49	3.04	5.46
600	0.43	0.56	0.68	0.81	0.94	1.19	1.69	2.33	2.98	3.65	6.55
700	0.50	0.65	0.80	0.94	1.09	1.39	1.98	2.72	3.48	4.26	7.64
800	0.58	0.74	0.91	1.08	1.25	1.58	2.26	3.11	3.98	4.86	8.73
900	0.65	0.84	1.03	1.21	1.40	1.78	2.54	3.50	4.48	5.47	9.82
1000	0.72	0.93	1.14	1.35	1.56	1.98	2.28	3.89	4.97	6.08	10.9
1100	0.79	1.02	1.25	1.48	1.72	2.18	3.11	4.28	5.47	6.69	12.1
1200	0.87	1.12	1.37	1.62	1.87	2.38	3.39	4.67	5.97	7.30	13.1

Geometric rectification of SPOT images
The geometric rectification method usually used includes polynomial method and differential method [3], which will be discussed briefly thereinafter

Polynomial rectification
The fundamental of polynomial rectification is bypassing the spatial relation of photograph, simulating the geometry distortion with translating, scaling, rotation, affine, skew and their combination, then presenting the relationship between original and rectified image using a second order or third order polynomial rectification is frequently used because its simplicity and cheapness. Polynomial rectification also can be used to registrate SPOT images to other sensor image .

From table 1, we can conclude that SPOT images with zero incidence angle can be rectified using, polynomial method if topographic undulation is less than 700 m; the acceptable undulation decreases with incidence angle increases; the SPOT image with >100 incidence angle can't be rectified using polynomial .

Digital Difference Rectification
for SPOT images , we set up the image plane coordinate system with its origin at the center of image and y axis parallel to flight direction, then the imaging equation of the I row is :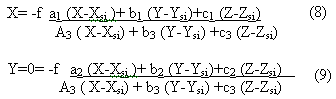

Where, (x, y) is the image point coordinate, f is the equivalent principal distance, (X, Y, Z) is the corresponding ground point of (x, y) , X_si, Y_si, Z_si are the exterior point elements in 1 row, a_i, b_i, c_i, (I= 1,2,3,) are the cosine of exterior angle elements in I row. When rectifying SPOT image, the exterior elements in center row are calculated through space resection of a single photograph, we select a point ( X, Y, Z) from Dem grid, substitution of it into eqs .(9) yield the y value, marking it as yp. the value yp suggest which row the current point is, combining the row number and the exterior elements of current row into Eqs. (8) and (9) and get the value ( x_l, y_l). If y_i is a infinitely small value, then ( x₁+y₁ +y_p) is the corresponding image coordinates of ( X, Y, Z), else we substitute y₁+y_p for y_p and calculate new y₁, this procedure will continue until y_i is infinitely small .

Digital differential rectification bases equation and perform point to point rectification. Theoretically, therefore, any SPOT image can be differentially rectified with high precis4e, but differential rectification has disadvantage of computation expensiveness and necessity of DEM. In fact, we usually have to rectify SPOT images with large incidence angle in high topographic undulation under the condition of no DEM to use, which is nearly impossible using polynomial rectification or differential rectification. We present a new rectification method-point by point rectification based on offset measurement-to resolve this problem.

Point by point rectification of SPOT image based on offset measurement
The essence of geometrical rectification is to remove the image point displacement, point by point rectification of SPOT image based on offset measurement is aimed to eliminate the offset between the corresponding points in SPOT image graphics model which is generated from scanned topographic map. The main steps are the following.

SPOT image course orientation - With SPOT image as the input image and the corresponding DRG as the reference image, only four corresponding points are selected, which had better distribute in the four corners of DRG. Then, one-order polynomial correction is carried out and the course orientation is finished.
Measurement of the offset in corresponding points - After courser orientation, the relative distortion, such as skew and scale, is left, which mainly results form the topographic, undulation. We superimpose DRG on to orientated image, search all the corresponding points which are visible clearly in either image, and measure the coordinates of these points using mouse. In the range equal to 1:50000 DRG, it is optimal to measure 70-100 points based on the consideration of the compromise between computation expensiveness and precision of rectification. All the coordinates of these points and the corresponding offset values are stored as a text file, which called " offset file ".
Point by point rectification - for every grid point P=(x,y) in which has been geocoded to a particular projection plane, we inverse it the oriented image grid system by adding a special offset? P=(?x, ?y). to determine the offset ? p, we search for four points in DRG from the offset file which hale the nearest distance to point P₁,P₂, P₃, P₄, and the corresponding offset in these points are ? P₁, ? P₂, ?P₄. we interpolate the offset ?P

By
:
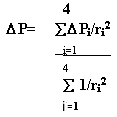
Where r_i denotes the distance form point P_i to point P, of courser, if point P already in the offset file ? is acquired directly from offset file. Thus the coarsely oriented image is geo-registerated to the DRG accurately.

The above algorithm has been developed as a software which has been successively applied to the National Buerua of surveying and mapping (NBSM)'s project-generation of 1:50000 satellite orthoimage.

An experiment has been carried out to check the precision of point by point rectification based on offset measurement . the SPOT image for experiment is imaged on Mar, 1999 in Lushan mountain are with incidence angle 1.9⁰, and the corresponding 1:50000 map index is H50-89-A. the maximum topographic undulation in test area is 1300 meters, the elevation in nearly one fifth are is above 1000 meters, and the Boying Lake is comprised in this map range, so searching clearly visible corresponding points is difficult, total 62 offset is measured and recorded, at last we measured the coordinated of 30 pairs of point the rectified image and the DRG, the error results are listed in Tab. 2.

Tab.2 precision check of point by point rectification based on offset measurement ( unit:meter) .

Point No	Error	Point No	Error	Point No	Error	Point No	Error	Point No	Error	Point No	Error
1	12.	6	21.1	11	13.	16	10.	21	19.	26	18.
2	11.6	7	8.5	12	22.	17	16.	22	19.	27	13.
3	18.	8	5.0	13	12.	18	8.8	23	14.	28	26.
4	23.	9	31.7	14	11.6	19	25.	24	15.	29	7.5
5	7.8	10	18.8	15	27.	20	9.5	25	13.	30	15
Mean square error: 16.8

Tab 2. indicates that this rectification method is feasible.

Conclusion
we formulated point displacement of SPOT images with different incidence angle due to topographic undulation, the formulate indicate that oblique viewing angle magnify the image point displacement from topography relief. The SPOT image point displacement resulted from 100-1200 meters topography undulation is calculated and naturalized to 1;50000 scale, the result is listed in Tab.1. from, the following conclusion can be acquired : if topography undulation is less than 700 meters; SPOT images with Zero incidence ( vertically illuminate ground ) can be rectified using polynomial method; with incidence angel increasing, acceptable topography undulation becomes small; when incidence angel is above 100, the image is not appropriate for polynomial rectification. Tab . 1 provides guide to select proper rectification based on offset measurement is proposed, which can be used to rectified nadir-off image in large topographic undulation are, a experiment on this new rectification method is carried out, the results suggests that the new rectification method is simply and feasible.

Reference

Li Deren, Jin Weixuan, You Jianshan , Zhu yixuan, Basic Photogrammetry. Press of Surveying and Mapping, Beijing, 1995, 1995, 56-60.
Li Deren, Zhen Zhaobao , Analytical Photogrammetry. Press of Surveying and Mapping. Beijing, 1992. 413-423.
Liu Haiyuan.
Geo Haiyuan. Geometrical Rectification of SPOT images. Journal of Remote sensing, Beijing, 1998, 15(3):33-35.