A way To automatic and High Precison Reconstruction of A Real 3D-City Surface

A way To automatic and High Precison Reconstruction of A Real 3D-City Surface

Jaan-Rong Tsay
Assistant Professor, Department of Surveying Engineering
National Cheng Kung University
University Road 1,China Taipei, 70101
Tel: (886)-6-2370876 ext. 838 Fax: (886)-6-2375764
E-mail: tsayjr@mail.ncku.edu.tw CHINA TAIPEI

Keywords: Real 3D-City Surface, Image Inversion, Wavelets, Fractal

Abstract
This paper proposes a wavelet-based algorithm to describe efficiently any 'real' signal with some distinctive properties which generally cannot be represented accurately by conventional methods that describe only a smooth approximation. This paper takes a real 3D-city surface as an example of such a signal and presents a way to automatic and high precision reconstruction of a real 3D-city surface using an image inversion method. For that purpose, some preliminary tests using simulated data and real aerial images are done to examine the applicability of the proposed algorithm. The test results show that high precision representation of a real 3D-city surface is realizable.

Introduction
The state-of-the-art computer science and technology enable an operational realization of the so-called 'virtual reality'. It causes a revolutionary progress on the representation form of surveyed object(s), namely from a conventional 2D-map to an easy-to-learn 3D virtual reality about surveyed object(s). A conventional 2D-map is not very user-friendly and loses much object information, whereas a 3D virtual reality model is really easy-to-learn and is a minified 3D model of surveyed object(s). To realize dynamical simulation analysis and representation of such a virtual reality of interest objects, many researches in the field of surveying aim also at automation technologies utilizing multi-sensor, multi-source and/or multi-temporal data (and information as well). For example, an automatic reconstruction and thematic information extraction of a geometric and radiometric 3D-city model is a hot topic.

This paper presents some preliminary study results. They aim at a research project, namely a (semi-) automatic reconstruction and analysis of a real 3D-city surface. The proposed models and algorithms should also be available for another kinds of real signals, e.g. a 3D sea surface, which have some distinctive properties that traditional methods can not describe exactly.

Properties of a Real 3D-City Surface
A 3D-city surface can be regarded as a continuous 'signal' of surface height or surface radiometric intensity, where the so-called 'signal' is generally interpreted as 'a sequence of digital data' (Meyer and Ryan, 1994). Those real signals such as a geometrical 3D-city surface have almost always the following four distinctive properties:

having local surfaces with (pseudo) break points or –lines,
multi-resolution,
various degree of continuity on different surface points, and
various fractal dimension, where detailed definition of 'fractal dimension' please see (Mandelbrot, 1982; Farge, et. al., 1993).

For example, (pseudo) break points or –lines often can be found on walls right round a building. Blocks of great and high buildings, blocks of small and low houses, visible surfaces of separate local trees/forests and some local naked natural earth surface as well compose a multi-resolution city surface with the properties (2) ~ (4).

An Idea
An idea aims at a research project, namely automatic and high precision reconstruction and analysis of a 'real' 3D-city surface having the above-mentioned properties (1) ~ (4), where one uses orthonormal fractal wavelets, e.g. the compactly supported Daubechies wavelets derived from minimum phase filters (Daubechies, 1992), to define a feasible functional model in the object space to describe a real geometric and/or radiometric city surface, and utilizes the principles of 'image inversion', 'sampling theorem' and 'least squares estimation technique’ under the application of the 'from-coarse-to-fine' strategy. The main idea is similar to the method of facets stereo vision (Tsay, 1998). It is a method for performing digital terrain reconstruction and ortho image computation, where digital images are the basic observations. It can also integrate in principle multi-sensor and multi-source data to provide reliable and accurate results for photogrammetry and remote sensing. The first draft of facets stereo vision was proposed publicly in 1987 (Wrobel, 1987).

The idea would further extend and improve the method of (Tsay, 1998) with the new capability for representing a real signal e.g. with the fore-mentioned properties (1)~(4). More explicitly to say, the idea aims for an automatic image inversion method to get object information. The method must be able to represent fractal geometry. For the present, only fractal geometry can correctly describe and analyze real natural objects. Therefore, fractal geometry is apparently the correct mathematics (Jaehne, 1991).

For that purpose, a thorough research of models and algorithms for representing a signal having the properties (1)~(4) is done, where some known simulated and representative 2D signals, chiefly 2D-city profile functions, and a 3D-city surface function are used to do the van study, especially about the characteristics and accuracy of the proposed algorithm for representing the above-mentioned signals.

Mathematical Models for Representing a Real Signal
The algorithm starts from the mathematical models based on some special orthonormal wavelets with the ability for displaying fractal signals. In fact, the compactly supported orthonormal wavelets of Daubechies display a fractal geometry (Kaiser, 1994).

Mathematical Models
An approximation of a real signal f with finite energy can be represented by:

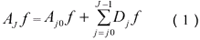
where

f and y. are an orthonormal father and mother wavelet function, respectively (Antonini, et. al., 1992; Daubechies, 1994; Meyer and Ryan, 1994).

The 2D-model can be expressed similarly to the equation (1), e.g. see (Mallat, 1998).

Models' Characteristics
In general, such models are based on those orthonormal fractal wavelets that cannot, in general, be written in a closed analytic form. Their graph and the other mathematical operations in practice, such as integration, differentiation, addition, multiplication, division, etc., can be computed with arbitrarily high precision by some specified methods, please see (Tsay, 1996).

Test Results using Simulated Data
For theoretical analysis, different types of simulated signals f such as city profile functions, city surface functions, step functions and so on, are used. In other word, each f is known in all tests. Therefore, one can determine the true error of A_jf and analyze its convergence characteristics. The conclusions will be given briefly as follows.

The algorithm is most effective and efficient, if a from-coarse-to-fine strategy is used to determine the locations of significant wavelet coefficients. The accuracy of such an approximation becomes better if a finer resolution (i.e. a larger j-value) is adopted, where j is a resolution index. The influence radius of the Gibbs phenomenon becomes smaller in a rate of 2^-j as the j-value becomes larger. The ratio of the maximal approximation error near a pseudo break point to the signal height difference at that break point is a constant. On the other hand, the Daubechies wavelet of 3^rd order is the best basis comparing to the other representative bases, namely the Haar wavelet, the Meyer wavelet and the Fourier basis. It is very suitable to describe different kinds of signals, e.g. a smooth signal, a rugged one and a signal with local break points.

Test Results using Real 3D-City Surface Data
The theoretical analyses are also done using a real geometrical city model in a suburb of Taipei. The model is measured on analytical plotter Leica BC3 using a stereo pair of aerial photos with a mean photo scale 1/5000, photo format 23cm x 23cm, and focal length 30cm. The analog photos are also scanned by photo scanner DSW200 with a pixel size of 25mm x 25m m. The measured 3D points in the stereo model are then edited to produce a geometrical surface in the test area shown in Figure 1. The geometrical surface is taken as a known real 3D-city surface that is used to examine the accuracy and characteristics of the wavelets-based approximation algorithm.

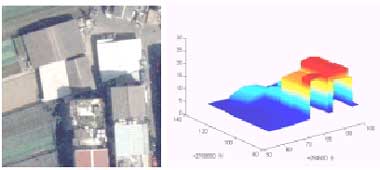
Figure 1. Aerial image in test area (left) and geometrical surface of the test area (right)

Some test results are shown in Figures 2 ~ 4. Apparently, approximation function A_jf can converge to f as the resolution becomes finer, namely the index j becomes larger. In addition, one can superimpose the digital image data on the computed geometrical surface and get a virtual reality of the 3D-city surface in test area, although the image information on all walls is evidently insufficient because only aerial images are used in these tests. Moreover, a dynamical stereoscopic view can also be made, if the related computer hardware and software are available. It is really an easy-to-learn and user-friendly 3D 'map'.

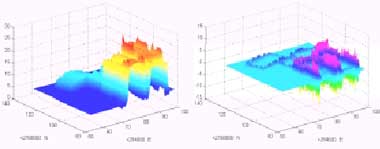
(a) Approximation A₀f (left) and its error function (right)

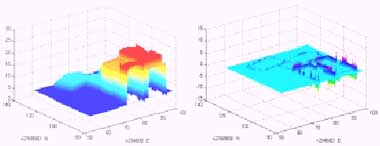
(b) Approximation A₂f (left) and its error function (right)

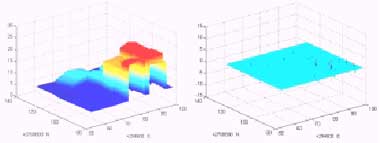
(c) Approximation A₄f (left) and its error function (right)
Figure 2. Approximations A_jf and their error functions with j = 0, 2, 4


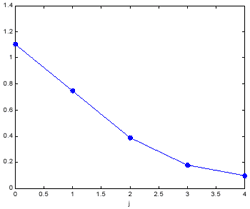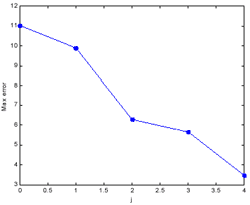Figure 3. Curve of the root mean square error (left) and maximal absolute error (right) of the approximations A_jf with j = 0 ~ 4

Figure 4. Virtual reality of the 3D-city surface in test area
A Way to Automatic Reconstruction of a Real 3D-City Surface
In accordance with those conclusions, a first draft of an algorithm for automatic reconstruction of a real 3D-city surface is depicted briefly in Figure 5. It adopts the idea stated in Chapter 3, where orthonormal fractal wavelets, the principles of image inversion, sampling theorem, least squares estimation technique, and a ‘from-coarse-to-fine’ strategy are utilized. In each level of the image pyramid, significant wavelet coefficients are automatically determined and selected and used as candidate unknown parameters for the lower level with finer resolution, so that an efficient operations are available.

Compute the image pyramid data.
Define approximation of DTM: horizontal plane or better data if available.
Compute a better DTM by the image pyramid method: From the top to the bottom level: For the top level:
Determine a_j0k and w_j0k ,"k.
Automatically select significant wavelet coefficients w_j0k , "k.Prolong the significant wavelet coefficients to the lower level.
For the lower levels:
Determine jk w for those candidates of significant wavelet coefficients.
Automatically select significant wavelet coefficients w_jk , "k.
Prolong the significant wavelet coefficients to the lower level.For the bottom level:
Determine w_jk for those candidates of significant wavelet coefficients.
Automatically select significant wavelet coefficients w_jk , ".k.
Output the computed DTM and ortho image and its covariance matrix as well.

Figure 5. First draft of an algorithm for automatic reconstruction of a real 3D-city surface
Conclusions
It is concluded that the proposed wavelet-based approximation algorithm can describe an entire geometrical function with local (pseudo) break points and/or –lines, where conventional piecewise representation is not needed. Some topics must be further and continuously studied, e.g. the first draft of algorithm shown in Figure 5 will be exactly developed and tested. Furthermore, a really 3D representation will be further studied, where one changes the current model Z(X,Y) with only one Z-value at a horizontal position (X,Y) to the other with the capability for representing more Z-values at a (X,Y).

Reference

Antonini, M., Barlaud, M., Mathieu, P., Daubechies, I., 1992. Image Coding Using Wavelet Transform. IEEE Transactions on Image Processing, Vol. 1, No. 2., pp. 205-220.
Daubechies, I., 1992. Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Philadelphia, Pennsylvania, pp. 194-202.
Farge, M., Hunt, J.C.R., and Vassilicos, J.C., 1993. Wavelets, Fractals and Fourier Transforms. Clarendon Press.
Jaehne, B., 1991. Digitale Bildverarbeitung. 2^nd edition, Springer Verlag.
Mallat, S., 1998. A Wavelet Tour of Signal Processing. Academic Press.
Mandelbrot, B., 1982. The Fractal Geometry of Nature. San Francisco: Freeman.
Meyer, Y., and Ryan, R.D., 1994. Wavelets – Algorithms & Applications. 2^nd printing, Society for Industrial and Applied Mathematics, Philadelphia, Pennsylvania.
Kaiser, G., 1994. A Friendly Guide to Wavelets. Birkhaeuser, pp. 183-189.
Tsay, J.R., 1996. Wavelets fuer das Facetten-Stereosehen. Deutsche Geodaetische Kommission, Reihe C, Dissertation, Heft Nr. 454, Munich, Germany, pp. 66-74.
Tsay, J.R., 1998. A New Algorithm for Surface Determination Based on Wavelets and its Practical Application. Photogrammetric Engineering & Remote Sensing, Vol. 64, No. 12, pp. 1179-1188.
Wrobel, B.P., 1987. Digital Image Matching by Facets Using Object Space Models, SPIE (=The International Society for Optical Engineering), 804, pp. 325-333.