|
Modeling rice growth from characteristics of
Reflectance spectra
Chwen-Ming
Yang*
and Muh-Rong Su
Agronomist
and Assistant, Department of Agronomy
Taiwan Agricultural Research
Institute, Council of Agriculture
189 Chung-Cheng Road, Wufeng,
Taichung Hsien,
Taiwan 41301, ROC
Tel: (886)-4-330-2301 ext.135,
Fax: (886)-4-330-2806
E-mail: cmyang@wufeng.tari.gov.tw
Keywords: Modeling, Rice Growth,
Reflectance Spectra, Vegetation index, Satellite
Abstract
A three-year (1996-1998) experiment was
conducted at Taiwan Agricultural Research Institute (TARI) Experimental
Farm, Wufeng to modeling of rice growth from characteristics of
reflectance spectra. The growth-waveband relationships were analyzed by
different reflectance transformation techniques and were compared among
several satellite sensors. The narrow-band ground remotely sensed spectral
data were acquired by a portable spectroradiometer and the broad-band
multispectral satellite inputs were simulated from the ground
measurements. Physical growth characters leaf number (LN), plant height
(PH), leaf area index (LAI), leaf dry weight (LDW), and aboveground dry
weight (ADW) were measured periodically. Results indicate a diverse
correlation coefficients between growth characters and different
vegetation indices and the wavebands set in satellite sensors. For linear
relationship, correlation with vegetation index (VI) was generally higher
than with single-waveband of satellites sensors. In a curvilinear
relationship, correlation between growth character (e.g. LAI) and VI (e.g.
NDVI) was greatly improved, and growth character was also better estimated
from reflectance of multi-waveband of satellite data. Results suggest that
rice growth may be reasonably assessed and monitored, either from the
ground or satellites, from characteristics of reflectance spectra when
proper wavebands are selected.
Introduction
Remote
sensing technology (RS) is currently an effective tool widely adopted in
various aspects of exploitation and management of natural resources. It
provides a timely detailed spatially distributed information allowing one
to measure, monitor, and analyze the time sequence changes of target(s)
possible. In agriculture, RS has been employed to the development of
precision farming for the better of crop production and environment
protection. Nevertheless, the surface reflectance spectra over a wide
range of objects and conditions should be identified and interpreted into
meaningful outputs prior to decision-making and applications. For such
purposes, data bank including spectral properties of physical
characteristics of crops and land cover and the corresponding mathematical
models have to be established based on ground truth. The in situ remotely
sensed datasets from aircraft or satellite can therefore be reasonably
resolved and reconstructed to the original state.
Yang and Su
(1997) simplified the relationship between LAI and the near-infrared
reflectance (756 nm) of rice canopy to the reverse of the Mitscherlich
function. Yang and Su (1998a, 1998b) found a curvilinear link between
growth characters (LDW and LAI) and normalized difference vegetation index
(NDVI) in rice crops from the ground spectral measurements. Su and Yang
(1999) further supported the fact by suggesting exponential formulae for
estimating the advancement of growth characters from NDVI. However, it
would be invaluable to learn whether the narrow-band models be applicable
to the broad-band measures of satellite sensors in the real world
applications.
The present study is to modeling of rice growth from
spectral characteristics of vegetative cover. The growth-waveband
relationships were analyzed and compared by different reflectance
transformation techniques among a number of satellite sensors. The
broad-band multispectral satellite inputs (Landsat-TM, Landsat-MSS, and
Spot-HRV) were simulated from the narrow-band ground measurements and rice
growth was assessed from physical growth characters investigations.
Materials and Methods
Rice (Oryza sativa L. cv. Tainung
67) were grown in the experimental farm of TARI, Wufeng (24° 02’ N, 120°
40’ E, elevation of 85 m) on a loam soil during the 1st and the
2nd crops in 1996-1998. Seedlings were machine-transplanted to
north-south rows with planting density of 1.92 × 105 hills
ha-1 , in 1996 and 1997, and 2.22 × 105 hills
ha-1 , in 1998, respectively. Each crop had 3 plots
(replicates) with plot size of 18 m × 11 m. Cultivation and fertilization
followed local cultural practices with furrow irrigation. Pest and weed
control was applied as needed to avoid pest and weed interference. Growth
characters (GC) of LN, PH, LAI, LDW, and ADW were measured periodically.
PH was taken by a ruler. LN was counted at the time of area measurements,
which was determined by a portable area meter (model LI-3000A, LI-COR
Inc., USA). LAI was calculated by the area of green leaves over unit area
of land. LDW and ADW were weighted after oven-dried at 80°C for 72 h.
Radiance from the incident solar radiation and vegetative cover
were acquired under the same sun conditions to calculate reflectance
spectra of rice periodically during the growing periods of 1996-1998. The
reflectance (%) of individual wavelength was calculated by dividing the
vegetation radiance measurements with the corresponding incident solar
radiation measurements (Yang and Su, 1997, 1998a; Su and Yang, 1999). A
LI-COR model-1800 portable spectroradiometer, with 2-nm bandpasses in the
range of 350-1100 nm, was used for the ground measurements. It was
connected to a quartz fiber-optic probe (LI-1800-10) and a remote cosine
receptor pointed downward in a nadir-viewing about 1.0 m above rice
vegetative surface. This distance was adjusted to plant height, by a
tripod, to scan the upward reflected radiation of canopy. Measurements
were made on clear or near cloudless days within 11:00-12:00 local
standard time and the average values were used. Characteristics
wavelengths of reflectance spectra were determined by using the first
order differentiation in cope with valley and peak observations of
spectral waves over six cropping seasons (Su and Yang, 1999). Wavelengths
at 554, 674, and 754 nm were selected as the characteristics wavelengths
(CW). They coincide with the absorption minimum and maximum of chlorophyll
and the near-infrared boundary of the chlorophyll red-edge, respectively.
The corresponding wavebands of LANDSAT-TM, LANDSAT-MSS, and SPOT-HRV
sensors to CW are listed in Table 1.
Table 1.
Comparisons of the spectral characteristics of different satellite
sensors with the characteristics wavelengths (CW) determined from
reflectance spectra of the ground measurements.
|
|
|
Landsat-TM |
Landsat-MSS |
Spot-HRV |
CW |
|
|
|
|
-------------------- nm
-------------------- |
|
|
450-520
(TM1) |
|
|
|
|
520-600
(TM2) |
500-600(MSS1) |
500-590(HRV1) |
554(GREEN) |
|
630-690
(TM3) |
600-700(MSS2) |
610-680(HRV2) |
674(RED) |
|
760-900
(TM4) |
700-800(MSS3) |
790-890(HRV3) |
754(NIR) |
|
|
800-1100(MSS4) |
|
|
|
|
Six VIs were selected from
the literature (Elvidge and Chen, 1995; Kanemasu, 1974; Rouse et al.,
1974; Tucker, 1979) defined as the followings: (1) sum vegetation index
(SVI): NIR+RED; (2) difference vegetation index (DVI): NIR-RED; (3) ratio
vegetation index (RVI): NIR/ RED; (4) green-red ratio vegetation index
(GRVI): GREEN/RED; (5) normalized difference vegetation index (NDVI):
(NIR-RED)/(NIR+RED); and (6) soil-adjusted vegetation index (SAVI):
(NIR-RED)× 1.5/ (NIR+RED+0.5). The broad-band inputs of satellite sensors
were simulated from the ground narrow-band reflectance (Table 1).
Correlation matrices were applied for GC and wavebands and vegetation
indices comparisons. Regression analyses were performed to generate
fitting-curves and equations in order to monitoring the comparative
changes of GC and wavebands and vegetation indices as plants aged.
Table 2.
Correlation coefficients for growth characters of rice and vegetation
indices (VI) calculated from characteristics wavelengths (CW) and the
simulated wavebands of different satellite sensors.
|
VI |
Leaf
Number |
Plant
Height |
Leaf area
index |
Leaf dry
weight |
Aboveground dry
weight |
|
Landsat-TM |
NDVI |
0.791 |
0.372 |
0.833 |
0.731 |
0.188 |
|
SAVI |
0.790 |
0.374 |
0.835 |
0.734 |
0.192 |
|
RVI |
0.815 |
0.187 |
0.881 |
0.744 |
0.071 |
|
DVI |
0.598 |
0.535 |
0.871 |
0.818 |
0.430 |
|
SVI |
0.284 |
0.648 |
0.683 |
0.699 |
0.609 |
|
GRVI |
0.830 |
0.024 |
0.800 |
0.631 |
-0.048 |
|
Landsat-MSS |
NDVI |
0.819 |
0.318 |
0.844 |
0.730 |
0.137 |
|
SAVI |
0.817 |
0.322 |
0.846 |
0.733 |
0.143 |
|
RVI |
0.829 |
0.181 |
0.873 |
0.734 |
0.054 |
|
DVI |
0.596 |
0.510 |
0.853 |
0.795 |
0.415 |
|
SVI |
0.053 |
0.623 |
0.470 |
0.522 |
0.645 |
|
GRVI |
0.854 |
-0.063 |
0.756 |
0.575 |
-0.142 |
|
Spot-HRV |
NDVI |
0.791 |
0.380 |
0.835 |
0.735 |
0.193 |
|
SAVI |
0.786 |
0.389 |
0.839 |
0.740 |
0.202 |
|
RVI |
0.817 |
0.200 |
0.881 |
0.747 |
0.073 |
|
DVI |
0.591 |
0.546 |
0.870 |
0.820 |
0.439 |
|
SVI |
0.279 |
0.654 |
0.682 |
0.700 |
0.616 |
|
GRVI |
0.854 |
-0.022 |
0.780 |
0.605 |
-0.107 |
|
CW |
NDVI |
0.800 |
0.329 |
0.825 |
0.717 |
0.155 |
|
SAVI |
0.799 |
0.333 |
0.827 |
0.718 |
0.159 |
|
RVI |
0.798 |
0.161 |
0.874 |
0.733 |
0.071 |
|
DVI |
0.630 |
0.475 |
0.865 |
0.798 |
0.379 |
|
SVI |
0.306 |
0.584 |
0.667 |
0.670 |
0.558 |
|
GRVI |
0.783 |
0.069 |
0.810 |
0.653 |
0.016 |
Results and
Discussion
Typical patterns of the measured GC during the growing
seasons were shown in Figure 1. The curves were analogous to seasonal
trends of NDVI in both crops (Figure 2), suggesting that NDVI was
sensitive to progression of vegetative cover and hence be a promising
parameter in estimating plant growth. The time-sequential changes of NDVI
and reflectance spectra were caused by the ‘environmental’ and ‘growth’
effects inducing significant changes in plant structure and morphology
during crop growth (Curran, 1983; Masoni et al., 1996; Sinclair et al.,
1971). The turning period of NDVI curve corresponded to the phase
transition, from vegetative growth to reproductive growth (Su and Yang,
1999). Because of the strong background effect and senescence, it would be
better not to use NDVI in the early and the late plant development.
Table 3.
Correlation coefficients for growth characters of rice and characteristics
wavelengths (CW) and the simulated wavebands of different satellite
sensors.
|
Waveband |
Leaf
number |
Plant
height |
Leaf
area
index |
Leaf
dry
weight |
Aboveground
dry
weight |
|
Landsat-TM |
TM1 |
-0.790 |
-0.339 |
-0.797 |
-0.690 |
-0.135 |
|
TM2 |
-0.754 |
-0.041 |
-0.608 |
-0.483 |
-0.187 |
|
TM3 |
0.838 |
-0.015 |
-0.718 |
-0567 |
-0.152 |
|
TM4 |
0.468 |
0.600 |
0.806 |
0.783 |
0.523 |
|
Landsat-MSS |
MSS1 |
-0.767 |
-0.073 |
-0.638 |
-0.512 |
-0.155 |
|
MSS2 |
-0.839 |
-0.017 |
-0.697 |
-0.543 |
-0.189 |
|
MSS3 |
0.372 |
0.599 |
0.723 |
0.715 |
0.555 |
|
MSS4 |
0.391 |
0.665 |
0.762 |
0.761 |
0.582 |
|
Spot-HRV |
HRV1 |
-0.757 |
-0.083 |
-0.632 |
-0.509 |
-0.148
|
|
HRV2 |
-0.839 |
-0.010 |
-0.711 |
-0.560 |
-0.165
|
|
HRV3 |
0.460 |
0.610 |
0.804 |
0.784 |
0.532 |
|
CW |
GREEN |
-0.678 |
-0.040 |
-0.530 |
-0.421 |
-0.199 |
|
RED |
-0.828 |
-0.052 |
-0.736 |
-0.590 |
-0.107 |
|
NIR |
0.503 |
0.538 |
0.801 |
0.764 |
0.470 |
Relations of GC and VIs
were examined by correlation matrix analysis. Generally LAI showed a
better correlation with these VIs among GC in all satellite inputs (Table
2). The relationships were further strengthened with curvilinear
functions. For instance, correlation between LAI and NDVI was improved in
an exponential relationship (Figure 3) with the determining factors
(R2 ) greater than 0.76. The predicted values of LAI were
linearly correlated to the observed values. Correlation coefficients for
GC and the simulated wavebands of different satellite sensors may be
positive or negative, whereas LAI had closer linkage in general (Table 3).
By stepwise regression to the second order of the spectral parameters,
estimation of GC can be formulated to exponential equations with
R2 greater than 0.53 (data not shown). Results indicate that
the normalized difference transformation technique is suitable for the
compensation of sun conditions and the estimation of rice growth. It
suggests a relative simple approach based on correlation between GC and VI
for estimating and monitoring the ground cover and growth performance.
This methodology is founded on the close linkage in vegetation spectral
characteristics and GC rather than purely empirical curve-fitting and thus
may be more universally applicable to a variety of applications. However,
such relationships may be changed and their availability will be reduced
under situations such as environmental stresses, pests infection, low sun
angle, and strong soil background effects.
The simulated results
also suggest that broad-band satellite data may be substituted for
ground-based narrow-band measurements if spectral characteristics of
wavebands are well-selected. Therefore, data bank established by
narrow-band ground truth is applicable to spectral inputs collected from
satellites in assessing plant growth of a crop. Due to many more
interacting variables, however, the spectral data measured from satellite
remote sensing are considerable more complicated than those from the
ground platform. Many important parameters in relation to atmospheric and
geographic calibrations need to be taken into consideration.
References
- Curran, P. J., 1983.
Multispectral remote sensing for the estimation of green leaf index.
Philosophical Transactions of Royal Society, London, Series A, 309,
pp.257-270.
- Elvidge, C. D., and Z. Chen,
1995. Comparison of broad-band and narrow-band red and near-infrared
vegetation indices. Remote Sensing of Environment, 54, pp.38-48.
- Kanemasu, E. T., 1974.
Seasonal canopy reflectance patterns of wheat, sorghum, and soybean.
Remote Sensing of Environment, 3, pp.43-47.
- Masoni, A., L. Ercoli, and
M. Mariotti, 1996. Spectral properties of leaves deficient in iron,
sulfur, magnesium, and manganese. Agronomy Journal, 88, pp.937-943.
- Richardson, A. J., C. L.
Wiegand, D. F. Wanjura, D. Dusek, and J. L. Steiner, 1992. Multisite
analyses of spectral-biophysical data for sorghum. Remote Sensing of
Environment, 41, pp.71-82.
- Rouse, J. W., R. H. Haas, J.
A. Schell, D. W. Deering, and J. C. Harlan, 1974. Monitoring the vernal
advancement and retrogradiation (greenwave effect) of natural
vegetation. NASA/GSFC Type III final report. Greenbelt, MD., USA, 371pp.
- Sinclair, T. R., R. M.
Hoffer, and M. M. Schreiber, 1971. Reflectance and internal structure of
leaves from several crops during a growing season. Agronomy Journal, 63,
pp.864-868.
- Su, M.-R., and C.-M. Yang,
1999. Estimation of rice growth from reflectance spectra of vegetative
cover. Journal of Photogrammetry and Remote Sensing, 4(3), (in press)
Tucker, C. J., 1979. Red and photographic infrared linear combinations
for monitoring vegetation. Remote Sensing of Environment, 8, pp.127-150.
- Yang, C.-M., and M.-R. Su,
1997. Analysis of reflectance spectrum of rice canopy. Chinese Journal
of Agrometeorology, 4, pp.87-95.
- Yang, C.-M., and C.-C. Ko,
1998. Seasonal changes in canopy spectra of sweet potato. Journal of
Photogrammetry and Remote Sensing, 3(1), pp.13-28.
- Yang, C.-M., and M.-R. Su,
1998a. Seasonal variations of reflectance spectrum and vegetation index
in rice vegetation cover. In: Proceeding of the 3rd Asian
Crop Science Conference. April 27-May 2, 1998. Chinese Society of
Agronomy. Taichung, Taiwan, pp.574-593.
- Yang, C.-M., and M.-R. Su,
1998b. Correlation of spectral reflectance to growth of rice vegetation.
In: Proceedings of the 19th Asian Conference on Remote
Sensing. November 16-20, 1998. National Mapping and Resource Information
Authority and Asian Association on Remote Sensing. Manila, Philippines,
pp.A-1-1-A-1-6.
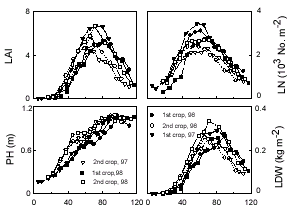
Days
after transplanting
Figure 1. Seasonal
changes in physical growth characters of leaf area index (LAI), plant
height (PH), leaf number (LN), and leaf dry weight (LDW) of rice (Oryza
sativa L. cv. Tainung 67) vegetative cover during the 1st and
the 2nd cropping seasons in 1996-1998.
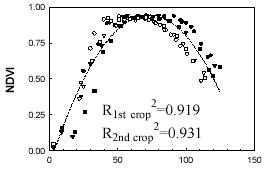
Days
after transplanting
Figure 2. Seasonal
changes of normalized difference vegetation index (NDVI) calculated from
characteristics wavelengths of rice reflectance spectra.
|
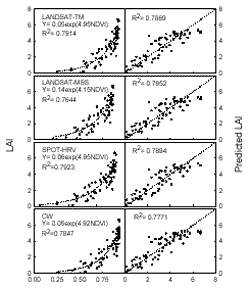
|
|
NDVI
|
Observed
LAI |
Figure
3. The
exponential relationships between leaf area index (LAI) and normalized
difference vegetation index (NDVI) and the linear correlation between the
predicted values and the observed values of LAI.
|


