| GISdevelopment.net ---> AARS ---> ACRS 1999 ---> Poster Session 3 |
Sunghee Kwak*, Dongseok Shin*, Tag-Gon Kim**
*Remote Sensing Research Division
Satellite Technology Research Center
**Department of Electrical and Science and Technology
Korea Advanced Institute of Science and Technology
373-1 Kusung-dong, Yusung-gu, Taejon, LIREA 305-701
Tel : (82)-42-869-8642 Fax : (82)-42 - 861 - 0064
E-Mail:shkwak,dshin}@satrec.kaist.ac.kr
Accurate camera modeling is one of the most important task for high precision topgraphic mapping using both satellite and aerial images. Unlike the aerial photos which show perspective views with a fixed focus, the linear pushbroom-type satellite images are obtained continuously along the track so that one focal point shoud be determined for each image scan line. Many camera modeling techniques for the linear pushbroom-type images have been published and most of them are based on the conventional collinearity equations with the position of a satellite most of them are based on the conventional collinearity equations with the position of a satellite as a function of time. Without thorough analysis of its modeling accuracy, the first order (linear) or the second order (parabolic) polynomials have been used for describing the time dependency of the position of a satellite. Although the camera model parameters such as satellite positions and attitude parameters as functions of time are estimated from ground control satellite positions and attitude parameters as functions of time are estimated from ground control points, initial values of the parameters to be estimated are required for the numerical iteration of points, initial values of the parameters to be estimated are required for the numerical iteration of non-linear least squares estimation. In this sense, some sort of algorithm should be used for determining valid initial position of satellite al, for example, the center of the image.
The orbit of a satellite is highly non-linear trajectory due to not only classical Kepler's motion theory but also several perurbation factors such as irregular potential field of Earth, lunisolar theory but also several perturbation factors such as irregular potential field of Earth, luisolar attaraction, atmospheric drag and solar radiation pressure. In general, satellite image users obtain orbital ephemeris data (satellite position and velocity vector table at a regular time interval) from the auxiliary data fields of image data. Since the implementation of high -precision orbit propagation algorithm for the satellite position determination is very expensive, it is desirable to either interpolate or extrapolate the given ephemeris data in order to obtain the position of satellite at the time of interest.
In this paper, we test and analyze the orbit interpolation and extrapolation accuracy by using simple Lagrangain polynomials. The followings can be determined and optimized from the results shown in this paper in order to obtain the interpolated or extrapolated positions of a satellite with less than a certain amount of errors required:
- the number of ephemeris sample points required:
- the minimum time interval of ephemeris samples required,
- the maximum time difference of the extrapolated position and the closed ephemeris sample point.
In practice, an orbit around Earth cannot be described accurately from the simple Keplerian motion due to various peturbation forces of which major contributions are non-spherical Earth gravitational effect, lunisolar attraction, air drag and solar radiation pressure. The effects of these perturbing forces depend upon instant location of the satellite, time of year, and even the size/mass/attitude of the satellite. Scientists have therefore dedicated themselves to determine gravitational potential distribution of Earth, time-location varying atmospheric conditions and solar activity as accurately as possible. These perturbation forces give both periodic and secular (progressive in time) effects to the satellite's orbit. Although only major secular effects can be considered for a long-term orbit planning, a short-term accurate orbit prediction must take the periodic effects into account. Cowell's method (Chobotov, 1996) which is widely used for accurate orbit prediction can provide a high fidelity integrator. This is a time-based numerical integrator which solves the second order differential equation for the forces upon a satellite at a specific time instance. We developed a high fidelity orbit propagator based on the Cowell's method by using the followings.
- EGM96 Earth gravity model up to degree and order 60 (NIMA, 1996)
- MSIS-1996 atmospheric model (Larson, 1992)
- 4th order fixed time step Runge-kutta integrator (Press, 1997)
Orbit Interpolation and Extrapolation by Using Lagrangian Polynomials
If we have n+1 distinct points given by (x0,y0), (x1,y1) .. (xn, yn) then is a unique fitting polynomial of degree n passing through these points. This polynomial, called the Lagrangian polynomial, is given by
Pn (x) = y0L0(x) +y1L1(x) + .. + ynLn(x)
Where
| Li(X) = | (x-x0) ..
(x-xi-1)(x-xi+1)…(x-xn)
Li(x)
(xi-x0)..(xi-xi-1)(xi-xi+1).. (xi-xn) |
Therefore, it we have n+1 ephemeris samples, 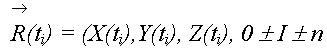
Whether they are
spaced with a regular time interval or not, we can obtain the following
three Lagrangian polynomials of degree n 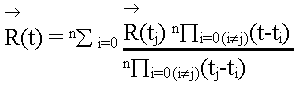
These fitting
polynomials are used for interpolating and extrapolating the ephemeris
samples. The process for calculating a satellite position vector at a time
within the ephemeris sample time interval is called interpolation. If the
time of interest lies out of the ephemeris sample time interval, the
process is called extrapolation.
Change Rate of Cartesian
Coordinate Component for Sun-Synchronous Orbit
Each component of a
Cartesian vector varies with a different rate along the orbit. The Z
component, for example, varies with a minimum rate in polar region and
with a maximum rate in equatorial region. The X,Y components show
completely opposite manner and their change rate depends also on the
longitude of sub-satellite point. In order to assess the accuracy of the
orbit interpolation and extrapolation for each Cartesian vector component
a complete one-day orbit should be tested and analyzed. In this paper,
however, we assess the accuracy by looking at "distance" of two different
vectors rather than each vector component. The overall change rate can
therefore be estimated by
||(X(t1 +D), Y(t1
+D),Z(t1+D))-(X(t1),Y(t1).Z(t1))||
In order to analyze the dependency of interpolation and
extrapolation accuracy to the instant position of the Sun-synchronous
satellite, we approximate the orbit to a circular and polar orbit and
assume non-rotating Earth without loosing much generality of a
sub-satellite point at time t1 be ((f,q), respectively. At some time
later, t2, a new sub-satellite point would be (f +D, q) and the overall
position change rate can be calculated as follows.
||(X2,Y2,Z2)-(X1,Y1,Z1)||
=||(rcos(f +D,) cosq, rcos(f +D)sinq,
rsin(f +D))
- (rcosf cosq, rcosf, sinq, rsinf)||
= rÖ[2(1-cosD)]
where r is
the radius of the orbit. The above equation clearly shows that the overall
change rate of Cartesian position of a satellite does not depend on the
instant of the satellite. Therefore, we can assess the orbit interpolation
and extrapolation accuracy by using any section of orbit regardless of its
location with respect to Earth fixed frame.
Experiment
Orbit Interpolation Accuray As the first
experiment, 1 minute interval ephemeris samples were interpolated by
Lagrangian polynomials with different degree (see the result in Figure
1).
Figure1. Lagrangian polynomial
interpolation using 1 minute sampled ephemeris (log scale)
Figure 1 shows that the addition of a small number of ephemeris
samples reduces the interpolation errors significantly (order of
magnitudes). As shows in Figure 1, the 3rd degree Lagrangian polynomials
with four 1-minute ephemeris data can be used for the orbit interpolation
with less than 10m error. Less than 1 meter interpolation errors can be
achieved by using the 4th degree polynomials with 5 samples.
Figure 2 shows the interpolation errors of lagrangian polynomials
with different degrees when the ephemeris data is sampled by 10,30,60 and
90 seconds. As the interval of the ephemeris samples are reduced, the
interpolation accuracy is improved as well. By comparing the results with
that in Figure 1, the 3rd degree Lagrangian polymomials (4 samples) are
accurate enough to obtain interpolation errors less than 1 meter if the
ephemeris samples are as fine as 30 seconds.
Figure 2. Interpolation errors depending on ephemeris time
step (log scale).
Orbit Extrapolation
Accuracy
Figure 3 shows the 10 minute (600 seconds) orbit
extrapolation accuracy using Lagrangian polynomials with 1 minute
ephemeris samples. As shown in the figure, orbit extrapolation errors
increase rapidly as the time gap increase. This means that the Lagrangian
polynomials are suitable for the orbit interpolation not for the orbit
extrapolation. The polynomials with the degree greater than 5 can be used
for 1 minute orbit extrapolation with less than 1m errors when more than
six 1-minute ephemeris samples are used.
Figure
3.Orbit extrapolation accuracy using 1 minute ephemeris sample.
Conclusions
In this paper, an orbit interpolation and
extrapolation technique using Lagrangian polynomials is suggested when
ephemeris data is available. This eliminate the necessity of implementing
a complex orbit propagation algorithm in order to obtain positions of a
satellite at a time of interest. The accuracy of the interpolation and
extrapolation is fully tested and analyzed in this paper.
The
orbit extrapolation technique is very useful for the determination of
satellite positions when real-time GPS data are provided from the
satellite. When the GPS-determined ephemeris data are provided at a
regular time interval embedded in the satellite image data, the satellite
positions in the time boundary cannot be determined by interpolation.
Therefore, the orbit extrapolation up to the ephemeris time interval is
required for the determination of satellite positions within the both ends
of the boundary regions.
Reference
- Chobotov, V.A. 1996, "Orbital Mechanics, 2nd Ed"., AIAA Education Series.
- Larson, W.J. and J.R. Wertz, 1992, "Space Mission Analysis and Design, 2nd Ed.", Miscocosm Inc & W.J. and J.R. Wertz, 1992,"Space Mission Analysis and Design, 2nd Ed.", Miscocosm Inc & Kluwer Academic Publishers.
- NIMA, 1996, "WGS84 Earth Gravity Model", http://164,214,2,59/GandG/wgs-84/geos.html
- Press, W.H.B.P. Flannery, S.A. Teukolsky and W.T. Vetterling, 1997, "Numerical Recipes in C, The art of computing", Cambridge University Press 4th revision.