Applcation of Multiscale Edge Detection to Speckle Reduction of SAR images

Applcation of Multiscale Edge Detection to Speckle Reduction of SAR images

Siriporn Dachasilaruk, Yuttapong Rangsanser, and Punya Thitimajshima
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkraband, Bangkok 10520
Tel: (66 2) 326-9967, Fax (66 2) 326-9086
Thailand
E-mail :kryuttha@kmitl.ac.th, ktpunya@kmitl.ac.th

Abstract
This paper describes a method of speckle reduction in synthetic aperture radar (SAR) images based on multiscale edge detection and wavelet thresholding. The edge regions are detected in each scale. The wavelet decomposition is performed on the logarithm of the image gray levels. A threshold value is estimated according to the noise variance in each subband and used for soft-thresholding. The image gray levels. A threshold value is estimated according to the noise variance in each subband and used for soft-thresholding. The image is then obtained by reconstruction from the thresholded coefficients, and the exponential function of this image gives the final filtered image. Experimental results on a JERS-1/SAR image showed that the proposed method provided a significant noise removal and preserves the sharp feature of the image.

1.Introduction
Synthetic aperture radar (SAR) technology has resulted in marked improvements in the spatial resolution images when observing a ground scene from aircraft or satellites and it can be used to estimate also features like the dampness of soil, the thickness of the forest, or the roughness of the sea. Nevertheless, SAR images are contaminated by multiplicative noise, resulted from the necessity of creating the image with coherent radiation. When an object is illuminated by of the incident radiation, the wave reflected from such a surface consists of contributions from many independent scattering point. Inference of these dephased but coherent waves result in the granular pattern known as "speckle". Therefore, speckle reduction is an important and essential procedure in most target detection and recognition systems.

Typical noise-non-edging methods are not well suited to preserve edge structure in speckled images. Classical operators are based on the local variance statistics (Lee, 1986; Burrus. 1987) and the multiresolution wavelet technique, the multiscale edge representation (MER) have been proposed as well (Rogers, 1998). Recently a novel approach for noise reduction due to (Donoho, 1995) has been established. It employs thresholding in wavelet domain. Moreover the same method can be used in a wide variety of related problems such as data compression and of SAR images such as in our previous work (Thitimajshima. 1998). An improvement is proposed in this paper, by applying the thresholding only to the wavelet coefficients that correspond to non-edge regions, and keeping edge-like regions intact.

The propsed method is described in Section 2, including the multiscale edge detection and wavelet thresholding techniques. Section 3 present two quantitative measures for evaluation of presented. Finally, section 5 provides a conclusion of the paper.

2.The Proposed Method
The basis of our proposed method, we first perform a segmentation to identify the edge regions based on multiscale edge detection, or less exactly, to identify the non-edge regions of the images. The speckle noise is the most observable in non-edge regions of SAR images. Then the wavelet decomposition is performed on the logarithm of the image gray levels. We find a simple and very effective way to estimate threshold value by taking the standard deviation in each highpass band and used for the soft-thresholding operation except the edge regions, in all highpass bands. The despeckled logarithmic image is then obtained by reconstruction from the thresholded coefficients, as illustration in Figure 1.

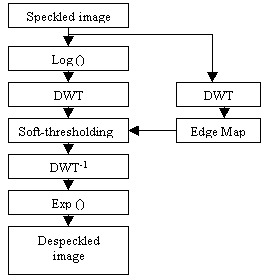
Figure 1: diagram of the proposed method.
2.1 Region Segmentation
The method of multiscale edge detection described in (Mallat, 1992) is used to find the edges. This wavelet is nonsubsampled wavelet decomposition essentially implement the discretized gradient of the image at different scales. Assume f(x,y) is a given SAR image of size MxN. At each scale j with j>0 and sof = f(x,y), the wavelet transform decomposes S_j-1 f into three wavelet bands: a lowpass band S_if, a horizontal highpass band W^H_i f and a vertical highpass band W^H_i f. The three wavelet bands (S_iF, W^H_i f, W^v_i f) at scale j are of size MxN, which is the same as the original image, and all filters used at scale I(j>0) are upsampled by a factor of 2j compared with those at scale zero. Form traditional edge detection, one knows that the points of sharp variations occur at local maxima (cal modulus maxima) of the gradient nrom in the direction of the gradient. However, we do not perform maximum detection and whenever processing has the drawback of high computation complexity that requires a long computation time. This evaluation can be characterized by the local Lipschitz regularity. That is, if the function f is Lipschitz a at point (x_o, y_o), then for (x,y) in its neighborhood,

M_jf(x,y)£K j^a (1)
where M_jf denotes the modulus of the wavelet transform at scale j and k is a constant. Since the Lipschitz exponents show the local regularity of image, it is a good indicator to identify these regions. We refer to edge regions that have high local variation of regularity among the neighboring coefficients. From (1), if the modulus of the wavelet transform is greater than K j^a it belongs to edge region, otherwise belongs to non-edge region.

2.2 Wavelet Thresholding
The theoretical formalizationof thresholding in the context of removing noise via thrsholding wavelet was presented by (Donoho, 1995). The idea is that, in wavelet domain, coefficients insignificant relative to the threshold are likely due to noise, whearas significant coefficients are important signal structures. There are two thresholding schemes: (a) hard-thresholding and (b) soft-thresholding. The operations are defined by:

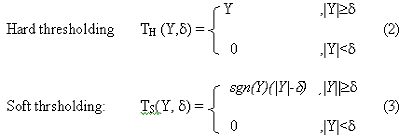
where the threshold d is an estimation from the wavelet coefficients Y. There is such a simple relative to find a threshold d. We consider d from estimation for the standard deviation of SAR image in wavelet domain as:

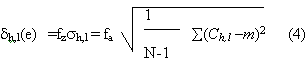
fs where N is the number of the iamge data, m the mean of wavelet coefficients C_h,l, with b represents each of the high-frequency bands (W^H_j f and W^v_j f) and l the number of decomposition levels, and f_a a thrshold factor systermatically assigned to 1/l.

Donoho shown that if the error or noise is bound then soft-thresholding is optimal. In general, the noise is uniformly distributed over all levels and show clearly in high-frequency bands. The soft-thresholding is therefore should be performed on all bands, with the exception to the lowest-frequency band. In this paper, we performed soft-thresholding in non-edge region of highpass bands. Moreover, in our method, the thresholding is applied only to the coefficients corresponding to non-edge regions.

3.Comparison Measures
Two quantitative measures were used to evaluate speckle reduction techniques, including the signal to mean square error ratio (S/MSE) and the mean value.

The Signal to Mean Square Error Ratio (S/MSE) ratio is used to quantify degradation in resolution. For best results, the S/MSE ratio should be maximized. If the original is l1 and the despeckled image is l2, it is defined as:

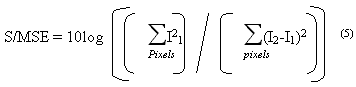
Another measure is the mean of the image. Speckle reduction techniques should in the image with a mean value close to that of the original one.

4. Experimental Results
A JERS -1/SAR, 256 x 256 image was used for the experiment under taken and the results are illustrated in Figure 2. Figure 2(a) shows the original SAR image. The despeckled image obtained by the wavelet thresholding, as descriged in (Thitimajshima, 1998), is shown in Figure 2(b). and the image resulted from the proposed method, with the parameters, l,K, and a set to 2. 30 and 2 respectively, is presented in Figure 2 (c). It is obvious that the sharp feature of the image was well preserved by this method.

Figure 2: Experiment on a JERS-1/SAR image. (a) Original image. (b) Despeckled image by the wavelet thresholding. (c) Despeckled image by the proposed method.
The quantitative comparison between these two methods is given in Table 1. As we can expect. the proposed method provided S/MSE higher than the wavelet thresholding, while maintaining the mean value closer to the original image.

Table 1: Quantitative comparison between the wavelet thresholding and the proposed method.

Images	S/MSE	MEAN
Original image	-	144.69
Wavelet thresholding	30.27	136.16
The proposed method	36.41	138.82

5. Conclusion
In this paper, we have illustrated that it is very efficient to associate edge information to a speckle reduction procedure. The proposed method improves the S/MSE, preserves mean and the sharp feature of the images. To achieve higher image quality, we should classify the image into more types of regions, such as edge regions, smooth regions, and texture regions, and use different threshold values adapting to each type of regions.

Acknowledgement
The authors wish to thank the National Research Coucil of Thailand (NRCT) of providing the satellite image data.

References

Burrus, J.M., Gimonet, R.A., and Perbos, J., 1987. SAR data filtering for classification. IEEE Trans. Geosci, and Remote Sensing, 25(5), pp. 629-637.
Donoho, D.L., 1993. Unconditional bases are optimal bases for data compression and for statistical estimation. Applied and Computational Harmonic Analysis, pp. 100-115.
Donoho, D.L. 1995. De-noising by soft thresholdign. IEEE Trans. Inform. Theory, 41 (3), pp. 613-627.
Lee, J.S., 1986. Speckel suppression and analysis for synthetic aperture radar images. Optical Engineering, 24(5), pp. 636-645.
Mallat, s. and zhong, S., 1992. Characterization of signals from multiscale edges. IEEE Trans. PAMI, 14(7), PP. 2207 2232.
Rogers, L.S., and Johnstone, C., 1998. SAR image despeckling using the multiscale edge representation. In: IEEE IGARSS'98, pp. 10-12.
Thitimajshima, P., Rangsanseri, Y., and Rakprathanporn, P., 1998. A simple SR speckle reduction by wavelet thresholding. In : 19th Asian Conference on Remote Sensing, pp. P-14-1-P-14-5.