Costrained Optimal Surface Tracking

Costrained Optimal Surface Tracking

Pakorn Apaphant
Scientist, Remote Sensing Division
National Research Council of Thailand
E-mail: pakorn@www.nrct.go.th

Abstract
The Constrained Optimal Surface Tracking algorithm (COST) is developed for object surface construction. The proposed algorithm makes use of both signal and feature data in its stereo matching method. A global optimization concept is applied in several matching method based on dynamic programming is investigated and extended in this research. Several types of primitive features are extracted and matched. The signal matching process is driven from the object space. The concept of dynamic programming for line following is applied here to determine the optimal elevation profile of a grid line. The object coordinates from the results of feature matching are used as weighted constraints during this process. Once the entire area is searched, the surface model is then constructed. The capability of the algorithm is evaluated through the test on aerial imageries. The experiments yield the impressive results.

1.Introduction
The construction of 3D urban area spatial models from aerial images is a difficult problem that continues to challenge the researchers in photogrammerty and image processing fields. The main problems are occlusion, large parallax range, and feature textures which are not amenable to the matching process. Feature based matching has been used to address these problems (Huertas and Modioni, 1986) (Ayachea and Faverjon, 1987) (Dhond and Aggarwal, 1989). However, if only matched feature information is exploited, it is not possible to reconstruct a surface model completely. Signal based matching has been used for solving such problems as well (Canny, 1986). This approach is often not successful when the assumption of moderate slopes and transitions are violated. Several methods are based on only one of these matching approaches.

In this investigation, some of the problems found in stereo matching, will be addressed by a strategy of combined signal and feature matching based on a global search technique. The sequence of steps for the feature matching component would entail extracting features along epipolar lines in the images, and matching the features by a dynamic programming based approach (Bellman and Dreyfus, 1962) (Otha and Kanade, 1987). The feature coordinates in the object space are then determined. After that a signal matching technique with feature constraints is applied to generate the elevation profile. The integrated algorithm is based on a line following method (Bethel et al., 1998). Once all profiles in a model are determined, the surface in the object space can finally be constructed. In this research, imageries from several scenes have been processed with results compared against manual collection.

2. Feature Matching
Several types features are extracted from images, along with their positions in epipolar space. Some features used in this research are already well defined from elsewhere, such as the straight line feature, and some are developed here such as end points of a plateau feature, and the spike point feature (Apaphant and Bethel, 1999). The features are extracted and tagged with attribute values. These values contain useful information for matching process. For example, the attributes of straight-line feature employed here are line orientation and length of a line. After the extraction process, the features for each epipolar line are identified and ordered along each line independently from left to right.

Correspondence metrics are defined in order to quantify the similarity of pairs of these features. In the matrix, the feature points on a density profile from one image represent stages (or columns) while the ones from the other image represent the possible states (or rows) for each stage. Each node formed by one feature point, I, on the left and one feature point, j, on the right yields a cost c(ij). The calculation of the correspondence cost c(ij) generally depends on the descriptive attributes of the pair. A good match yield low cost, a poor match yields a high cost. A very high non-correspondence cost, c(nc) is assigned when the two considered feature points are determined to not correspond. The costs are computed for every combination. A two dimensional array of the correspondence cost matrix can then be constructed (Figure 1).

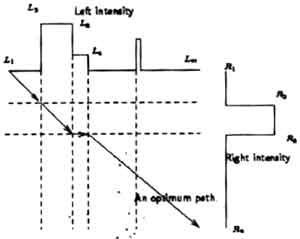
Figure 1: Feature matching by dynamic programming
Assume that the correspondence is known at the first and last column. The task is then to find the least cost path from the start point to the end point. Some stabilizing constraints are typically included to decrease the number of admissible paths. These constraints arise from the fundamental theory of stereo vision (Ballard and Brown, 1982).

By defining fi(j) as the minimum cost of the partial path from the first point to node (I,j), then fi. (j) is given by Equation1. For each node (i,j), the node (i-1,k) that gives the minimum partial path fi(j) is recorded.

f_i(j) =mink[c((i-1,k), (i,j)) + f_i-1(k)], where 1£k £ n (1)
Finally the optimal path can be found by backtracking from the last node (m,n) until the first node is reached. The path that sequentially connects these minimum nodes is the optimal path. The assigning of left and right to stages and states is arbitrary and in fact we do it both ways, with a consistency check between the two. Once the match pairs are determined, object coordinates of feature points can be computed by using the collinearity equations.

Profile Tracking
Correct correspondence at the signal level needs to be accomplished to supplement the results of feature matching. The results from feature matching are only the coordinates of some points on extracted features. It thus represents only a sparse surface model. The proposed signal matching algorithm is driven from ground space so it is, initially, completely separate from the feature matching process. A regular grid is first established in object space. The method is designed to find the elevation profile along each gridline.

The VLL concept (Bethel, 1986) is adopted for use in this algorithm. Each grid line is extruded vertically to create a 2D grid in a vertical plane. Grid cells are defined by a planimetric interval and a vertical interval. Each cell in this array is projected into the left and right photos and a match coefficient over a small region surrounding the point. This process is done similarly for all points in a grid profile creating a vertical plane of grid cells, each characterized by a match coefficient. If these coefficients are scaled into gray levels for display, then one can visualize the process. The picture of an approximated elevation profile would appear as a line on a noisy background (Figure 2).

Figure 2: An approximated elevation profile
The dynamic programming technique for line following (Bethel et al., 1998) is applied here to search for the otimal profile from a correlation-based cost matrix. This variation of the technique uses path length as the stage, and direction as the state. The technique that we are using here was originally designed for tracking a line in 2D which minimizes the sum of costs encountered while going from the starting poing to the ending point of the line. This is similar to our requirment but we wish to restrict out search to paths which only move from left to right. An elevation profile does not move in one direction and then move backword. Therefore, at a certain point (x, y), there are five possible directions to move to. The path propagation mask is stepped exhaustively through the cost matrix once for each increment in path length, from 2 to the maximum length. The decision must be made for each of the five locations in the path propagation mask at each position of the mask. The optimal elevation profile from the starting point to the ending point whose cost is minimum be determined as in Equation 2.

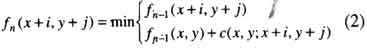
where c(x, y; x+i, y+j) = A local cost required to pass through points (x, y) to point (x+i, y+j). fn(x, y) = The minimum cost required to pass thtough point (x, y) to end an end point at current (or shorter) path length = n.

During the optimization process, the object coordinates from matched features are used as constraints. The signal-derived profile in the vicinity of such features may be in error. Conversely, the dynamic programming search would try to pass through the feature points if they were assigned a very low cost. We can then compel or the search algorithm to pass through features by providing a very small cost to any cells which represent feature points. Once the optimal profiles from all grid lines are obtained, the object surface model can then be reconstructed.

4. Experiments
A number of experiments have been done to develop, test and verify the validity of this technique. This paper present some experimental results determined automatically by the proposed matching algorithm. An object surface model constructed from a neat area of a rural scene (Figure 3) is illustrated in Figure 4. The neat area of an image in Figure 5 covers an urban scene. Its object surface model is shown in Figure 6.

Figure 3: Left and right image of a rural scene

Figure 4: Surface model of the rural scene using COST

Figure 5: The neat of an urban area scene

Figure 6: Objected surface model of the urban scene using COST
The capability of the proposed DSM extraction technique can be evaluated through the accuracy of the experimental results. They were compared with the results from other approaches. The studied area from his experiment was also extracted by using the ATE procedure from a commercial photogrammetric workstation. The elevation values from sets of points derived by these two automatic terrain extraction methods are compared to the manual collections. Assuming that the data collected manually is error free, the distribution of the errors in this experiment is shown in Table 1. These results indicate that our approach, while promising, is not yielding results up to the quality of existing tools.

Table 1: Comparison of different types of error measurement

Error Type	Rural scene (m.)		Urban scene (m.)
Error Type	ATE	COST	ATE	COST
Arithmetic Mean Error	0.21	0.31	-0.12	1.56
Mean Error Magnitude	0.48	0.88	1.12	1.99
Root mean Square Error	1.33	1.86	2.33	3.82

5. Conclusions
This paper has described an integrated stereo matching technique for object surface reconstruction. The matching problem is addressed the integrating of both signal and feature based. The classic dynamic programming for feature matching is modified and enhanced to integrate signal and feature matching into a simultaneous surface determination. The initial global error statistics indicate that the methods offers promising potential in exactly the circumstances where area correlation is weak. This approach can be further developed with other features, other match criteria, and the better search method to yield even better results in the future.

References

Apaphant, P. and Bethel, J., 1999. Integration of feature and signal matching for object surface reconstruction In; Proceedings of ISPRS-International workshop on mobile mapping mapping technology, Vol. XXXXII, Part 2W1, pp. 7A1-1 -7A1-7.
Ayache, N. and Faverjon, B., 1987. Efficient Registration of Stereo Images by Matching Graph Description. International Journal of Computer Vision, pp. 107-131.
Ballard, D. and Brown C., 1982. Computer vision, Prentice Hall, Inc. Englewood Cliffs, NJ.
Bellmna, R. and Dreyfus, 1962. Applied dynamic Programming. Princeton University Press, Princeton, NJ.
Bethel, J., 1986. The DSR11 Image Correlator. In: ACSM-ASPRS, Annual Convention, Wasthington DC., Vol. 4,pp. 44-49.
Bethel, J., Mikhail, E., Kim, K., and Marshall, J. Intelligent map understanding -Automated feature recognition and delineation. Technical report, School of Civil Engineering, Purdue University, IN.
Canny, J., 1986. A computational approach to edge detection. IEEE Transactions on pattern on pattern analysis and machine Intelligence, PAM1-8:429-455.
Dhond, R.R. and Aggawal, J.K. 1989. Structure from Stereo- A Review. IEEE Transactions on Systems, Man and Cybernetics, 19(6), November -December, pp. 197-219.
Huertas, A. and Medioni, G., 1986. Detection on intensity changes with subpixel accuracy using laplacian-Gaussian masks. IEEE Transactions on Pattern Analysis and machine Intelligence, PAM1-11(2): 121-136, July.
Ohta, Y. and Kanade, T., 1985. Stereo by Intra- and Inter-Scanline Search using Dynamic Programming. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAM1-7, March, pp. 139-154.