GISdevelopment.net ---> AARS ---> ACRS 1999 ---> Poster Session 6 Interferometric Processing of SIR-C Data for DEM Generation in Mt. Kunlun, West China Wang Chao , Zhang Hong , Pan Guangdong , Yang Qingyou Institute of remote Sensing Applications, Chinese Academy of Sciences, Beijing 100101 Tel:+86 10 6488 9546 Fax:+86 10 6488 9786 E-mail: cwang@public.bta.net.cn Abstract The Spaceborne Imaging radar (SIR-C) onboard the space shuttle Endeavor acquired interferometric synthetic aperture radar (InSAR) data over Mt. Kunlun, West China, during its second flight in Oct. 1994. An interactive INSAR data processor is developed for DEM Generation from SIR-C interferometric data. The main procedure includes coregistration of SLC data, phase unwrapping by weighted least-squares algorithms, InSAR parameter estimation with ground control points, Image slant range to ground range correction with resulting height information. The rms error of resulting DEM in Karakax test site of Mt. Kunlun is around 16m. Introduction During last decade interferometric synthetic aperture radar (InSAR) shows as powerful technique for three dimensional information retrieval of earth surface. INSAR takes advantages of not only capabilities of conventional SAR systems but also phase information of radar signals, which provides geometric information of surface. Since late 1980’s InSAR becomes one of advanced topics of remote sensing. In Oct. 1994 during the second SIR-C mission, repeat-pass interferometry was experimented from its 8th mission days. Interferometric data was acquired over several test sites, including Karakax Valley of Mt. Kunlun, West China. In this study, the SIR-C interferometric data was processed for DEM generation over Karakax Valley test site. Test Site and Data Description The properties of this data set are given in table I. Table I Parameters of SIR-C interferometric  data in kunlun , xinjiang Data take 143.40 159.40 Acquisition date 941009 941010 Platform altitude (km) 213.6539764 213.4776459 Latitude N36.0724678 N36.0473557 Longitude E79.1982880 E79.2181244 Band L L Wavelength (m) 0.2422721 0.2422721 Incidence angle (degree) 50.681 50.780 Polarization V V V V Azimuth pixel spacing (m) 4.4907508 4.4907508 Range pixel spacing (m) 3.3312409 3.3312409 Slant range(near) (m) 318.5835876 318.5835876 Description of technique The processor is divided in the following blocks: image registration, interferogram generation, flat-earth phase removal, phase unwrapping, interferometric parameters estimation, and DEM generation (see Fig 1). (1) Conregistration. The image conregistration is performed in two stages: coarse and fine registration. Coarse registration is based in a cross correlation in a window at the center of the scene. Fine registration must compensate the pixel misregistration and its variation along the image with an accuracy of sub-pixel. 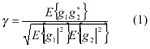The interferomeric coherence is defined by g1and g2 denote pixel values in each of the two images (see Fig.2) respectively and E{} denotes expectation value. (2) Interferogram generation. The interferogram is generated by multiplying one image by the complex conjugate of the other one. The order of the multiplication is determined in order to assure the correct sign of the phase. (3) “Flat earth” phase removal. The "flat earth" phase is computed by measuring the dominant fringe frequency in azimuth and range directions of the interferogram, and then it can be removed, so that the remaining fringes are due only to the relief. (4) Phase Unwrapping. Phase unwrapping is the reconstruction of a function on a grid given the value modulo 2p of the function on the grid. In order to reduce the phase noise and to facilitate the phase unwrapping , the interferogram is filtered and enhanced . The next step is phase unwrapping. In the last few years an increasing interest has been devoted to phase unwrapping. In our study, weighted least-squres algorithm using discrete cosine transform and branch-cutting algorithm are tested. 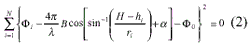(5) Interferometric parameters estimation.Since ERS-1/2,SIR-C has less precise tracking of the orbit and basseline parameters, the InSAR parameters estimation from ground control points is performed using least squares algorithm as equation (2): where, B is baseline, Fi is absolute interferometric phase at point (hi,ri). (6) DEM generation. The conversion process between the unwrapped phase in the slant range and a geocoded DEM is carried out in two steps. First, the relation between phase and height can be set up by two ways, ground control points or interferometric parameters. The resulting height map is given in slant range coordinates. The second step is geocoding, the transformation onto a cartographic reference system of the slant range height map. Geocoding was done using the orbit information to project the slant range image over the ground. Results and Conclusion Figure 3 shows the interferogram of karakax site after flat-earth phase removal. The estimations of interferometric parametric is shown in table II. These results are calculated by 15 ground control points, which are selected from 1:5000 relief map of study area. The unwrapped phase calculated by weighted least –squares algorithm is shown in Figure 4 , and Fig. 5 is DEM of Karakax after geocoding. The accuracy of karakax SIR-C DEM’s is evaluated by ground control points, and the average accuracy measured is 16.14m rms. Table II the estimation of interferomeric parameters of  SIR-C data of karakax area Baseline (m) 140.849 Baseline rate -0.0287121 Baseline angle (radian) 0.866694 Baseline angle rate 0.0 Platform altitude (km) 220.023 Platform altitude rate -4.20959e-05 Constant phase (radian) -14.7618 Parameter quality 2.38291 A SAR interferometry processor and its main algorithms along with some results has been presented. It is capable to process quadrant size images although phase unwrapping keeps being the critical step depending on the scene relief. Further work will be oriented to adopt a more rapid InSAR processing strategy. Acknowledgements This work is part of SIR-C/X-SAR program and supported by Chinese Hi-Tech( 863) program and National Natural Science Foundation of China(49781001). The authors acknowledge the NASA/JPL for providing the SIR-C images. Reference H.A.Zebker, C.L.Werner, P.A.Rosen , and Scott Hensley, “ Accuracy of Topographic Maps Derived from ERS-1 Interferometric Radar”, IEEE Trans. Geosci. Remote Sensing, Vol.32, pp. 823-836, 1994 S.N. Madsen, H.A.Zebker, and Jan Martin, “ Topographic Mapping Using Radar Interferometry : Processing Techniques”, IEEE Trans. Geosci. Remote Sensing, vol.31, pp. 246-255, 1993 Wang Chao, “ DEM Generation of SIR-C Interferometric data”, Journal of Remote Sensing (in Chinese with English abstract), Vol.1, No.1, pp 46-49,1997 Daniel Carrasco, Susanna Sanz, Ricardo Sousa, and Antoni Broquetas , “The Developing of a Wide Area Interferometric Processor” , Fringe’96 Wang Chao, Zhang Hong, Pan Guangdong and Yang Qingyou, “ Retrieval of DEM from SIR-C Data in Kunlun Mountain, West China, Proceedings of IGRASS’99, Hamburg, Germany, 1999 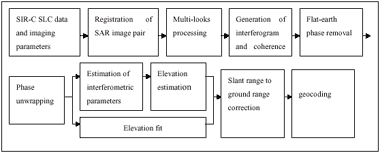Fig. 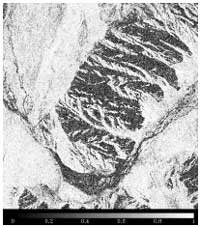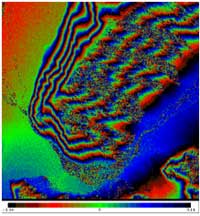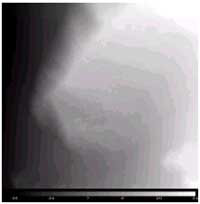1 Framework of interferometric SAR data processor for DEM Fig.2 The interferomeric coherence  map Of Karakax site Fig.3 the interferogram of Karakax site after  flat-earth phase removal Fig.4 The unwrapped phase calculated by  weighted least –squares algorithm Fig.5 SAR image of Karakax  area overlaid with DEM