Optimization of Building Triangulated Irregular Network

Optimization of Building Triangulated Irregular Network

Tu Jianguang, Zhang Mu, Bian Fuling
Informatics Engineering School. WuHan Technical University of Surveying and Mapping

Abstract
this paper puts forward several optimizing methods in building Triangulated Irregular network in traditional ways according to the questions appeared in actual projects. These methods can improve the efficiency of application based on Digital Terrain Model.

Terrain information is different from land use, type of soil, geological unit and so on. So commonly it is explained as a continuously varying surface which cannot be simulated approximately by a choropleth map. So in order to implement terrain analysis, it is an efficient way that simulates the configuration of the earth's surface with a group of digital data representing locations on the land surface - Digital Terrain Model (DTM).

DTM can be used for all kinds of route designing, engineering evaluation and production of sectional profiles, etc. it has brought great benefits in many applications such as analysis of land use, planning and management, disaster prediction and the like.

There are many ways to build DTM. Triangulated Irregular Network (TIN) is the simplest and the most applicable one among methods directly using dispersing data.

I. The necessity of fast building TIN
As the functions mentioned above, building DTM with original observations can be applied to surveying-engineering or other fields that can be used to implement a series of applications such as interpolating contours, calculating cut and fill, describing profiles, etc. Building TIN is the foundation and key of this kind of method, its quality and efficiency can affect subsequent works. It takes long time in writing and running programs because of the big amount of computation in building TIN and complex data structure.

In addition, the more advanced the means of obtaining data it uses, the more numbers of data it collects. As a result, the speed of building. TIN will get shower and slower. Optimization of a building TIN is the urgent affair so as to improve the program efficiency.

II. The principle of building TIN
On concerning of mathematics, what we will do is searching for an extending point C, which makes the vertex angle c's degree to be the maximum of all values larger than the threshold. Point C is generated from side AB to become a extending point. At the same time the point C and the point M must be located to different sides of AB (see figure 1). How to find the extending point rapidly becomes the key process, it will spend almost 90 percent of time in building TIN. We may divide data into some rectangle blocks in order to optimize building TIN.

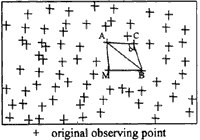
Figure 1
III. The data blocking in building TIN
Data blocking is the most efficient way to shorten the time of building TIN. So it can be adopted widely. As we usually know, the original observation data are disorderly, and the distribution of data is irregular. But when searching for an extending point, the final result is only related to the surrounding data points. In order to find the needed data points from the abundant original data, we must divide these original data into some blocks. There're many ways of data blocking, and different data structures, so we should be use different data blocking ways. In general there are three ways of data blocking as the following:

data blocking with overlapping
to divide the whole area into several blocks with overlapping parts could be satisfy the continuity of the data (see figure 2). This method is suitable to meet the conditions of building network. When we build TIN on different blocks, the relationship and data structure are very complex because there're overlapping areas within each other. So it is hard to complete building TIN. Moreover, the size of the block and the overlapped area are not easy to define, thus we need to do some adjustment base on data distribution mode (sparse or dense). Under particular conditions, some TINs could be missed. If the data distribution is uniform, the efficiency of building network will be higher. So this method is adopted in some cases.

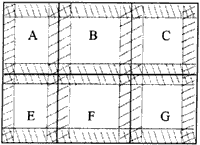
Figure 2
the method of non-overlap single area management.
To divide the whole area into some little areas which are neighboring and non-overlap (see figure 3).

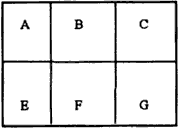
Figure 3
When we use this method to build net, there're no need to consider the effects of the surrounding area. We should record the outmost net border when we build the net of each area. After all blocks are built, it connects the borders of neighboring areas, so we get the TIN of the whole area. Because we deal with each area separately when building the net, the data structure is very simple, and the efficiency of building net is also very high, so it's relatively easy to handle. But because of lacking consideration of the surrounding areas when building the net, it makes the TIN at neighboring areas is not the best one (doesn't build the net based on the biggest angle principle) thus some long and narrow triangles will appear (See figure 4). If there's no need for high quality but for high efficiency, we can use this method. But on the other side, we should adopt blocks with suitable size, or may miss some TINs or create too many long and narrow triangles.

Figure 4
the method of non-overlap multi-area disposal According to some problems of the former tow kinds of methods, we put forward to the method of non-overlap multi-area disposal. Because there is not overlap among areas, the data structure is simple and it is convenient when we use this method t build net. Multi-area disposal method avoids the appearance of the long and narrow triangles in neighboring areas, and has little effect by the size of blocks. It gets a better combination between the complexity of data structure and the calculating quantity, so it's been widely used. Now we will describe this method of building net.

IV. using non-overlap multi-area disposal to build TIN

1. Confirmation of the searching scope
We start from a given triangle, make one side as the extending side, search other points of the whole area scope, make the vertex angle which created by this point and the extending side is the biggest one. We can't consider the vertex angle created by near points is the biggest one. As the following figure, the side of AB is the starting side, points of M and C are the extending points, points M is nearer to AB than point C to AB, but ÐAMB < ÐACB Then, what's the relationship between distance and vertex angle?. In order to explain it, we will discuss it in two ways:

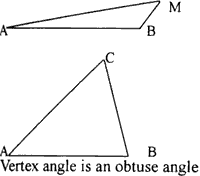
Figure 5

Vertex angle is an obtuse angle (<c >=900)
Under this condition, the circle whose diameter is the extending side includes all points that can form obtuse angle. That is to say, if the vertex angle of the triangle composed of vertex point C and another two points A, B is no less than 900, the point c must locate inside the circle whose diameter is AB, on the contrary, if the vertex angle is less than 900, it must locate outside the circle (see Fig.6). Therefore, if we can find a vertex point C that makes the vertex angle larger than 900, then we can decide the circle to be the only searching area. The point makes the biggest vertex angle in this range is the extending point we're searching for Fig. 7 indicates a case in details. The circle whose diameter is segment AB intersects with block B3, B4, C3, C4, D3 and D4. Because D3, D4 locate on same side with point M, they don't need to be searched. So in this searching process the point whose vertex angle is the biggest obtuse angle that satisfy all searching conditions is the exact extending point within either block of B3, B4 C3 and C4. because the computation of deciding whether one point is locating in the circle or not is very difficult, we often calculate in the circumrectangle of circle. If we cannot find a point that can satisfy the searching condition, we continue to search other points according to the method of acute angle. During the process of building TIN, researching within areas of corresponding circumrectangle will greatly save the time of building TIN. The denser the points are, the better the effects is.

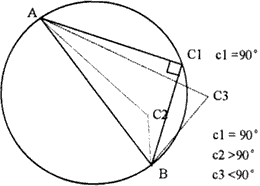
Figure 6

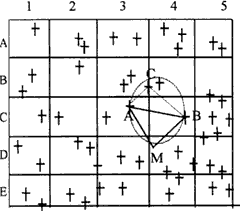
Figure 7
While vertex angle is acute angle (Ðc<900)
As shown in Fig.8, a is acute angle, then on condition that the locations of point A and point B are known and a is a fixed angle, what's the maximum distance of point C to point A or point C to point B. in other words, while vertex angle is fixed, what's the maximum one between distances of point C to point A or point C to point B in all possible locations of point C? In practice, we can draw this conclusion that the maximum does exit. According to the figure, there is the following mathematical equation.

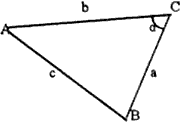
Figure 8
Cosa=(a²+b²-c²)/(2*a*b)
Where a, c are fixed , a or b is what we want. Suppose a is the function of b, that is a = F(b). using the following function:

a²+b²-c²-2abcosa=0
Get derivative of b, and let F' (b)=0
So 2aF' (b)+2b-2acosa -2bF' (b)cosa=0
And we get Cosa=b/a.

That is to say, while a is a fixed constant, and a and b satisfy the equation Cosa=b/a, we get the maximum of a, as shown in the following figure:

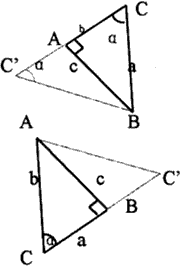
Figure 9
It is very easy to find that while AC^AB, we get the maximum of a (that is the maximum distance between C and B). Since A and B are points that could be interchanged, while BC^AB, we get the maximum of b(that is the maximum distance between C and A).

Because a and c are fixed, we know that max(a)=max(b)=csina

So when we are looking for extending points, if we find a point C, and compose a triangle whose vertex angle is less than 900 with point A and point B, then we can get two circles whose centers are points A and B, diameters are maximum of a and b respectively. The intersection of the two circles is the area that we want. Generally, the circumrectangle of the area is used as searching area in order to reduce computation (see fig.10).

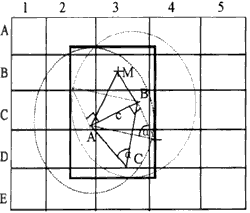
Figure 10
DAMB is a given triangle, and has found an extending point C (a less than 900). A circle that takes point A as center and max(a) as radius covers:

A2, A3, B1, B3, B3, C1, C2, C3, C4, D1, D2, D3, D4, E2, E3.

The circle that takes point B as center and max(B) as radius covers:

A2, A3, A4, B2, B3, B4, C2, C3, C4, D2, D3, D4, E2, E3, E4.

The rectangle that overlays the two circles covers:

A2, A3, A4, B2, B3, B4, C2, C3, C4, D2, D3, D4, E3, E4.

According to the extending-point-different-side request (that is point C and point M distribute of different side of line AB), the searching region should be:

B4, C2, C3, C4, D2, D3, D4, E2, E3, E4.

The point that has the biggest angle in searching regions is the extending point generated by line AB. In general practical operation, first it will search obtuse angle region, then the acute region. Each time it completes a block searching, it calculates the searching region again to decrease it.

2. confirmation of blocks
The main purpose is to record which region to be searched and to make sure if the whole block satisfy the different-side request. The blocks substitute for points greatly reduce the computation. The shape of blocks could be rectangle or square in proper size. Generally speaking, there're approximately 100 points each block. Too many or too few points can't meet the purpose of dividing blocks. Though they won't affect the quality of the network, the efficiency of building TIN will be influenced. In general the data will be blocked in data pretreatment process.

V. Steps on non-overlapping multi-region building TIN
Because general process of building network has been discussed in another paragraph, this paragraph will give simple descriptions on non-overlapping multi-region building TIN.

Data pretreatment process
1. Removing redundant points and reducing unnecessary computation.
2. Blocking the data, making proper size of each block.
3. Assigning each block a flag value to show if the block has been searched.
Building network process
1. finding the first triangle, making its longer side to be the original extending side.
2. Making the original side to be the diameter of a circle, then searching within areas of the circumrectangle of the circle. After finishing searching, if a point is found that could make the angle bigger than 900, then it's the extending point to be the original side. Starting with the longer side of the new triangle, repeat step b. Or, starting with step c.
3. If it could find no point or acute angle point within areas of the circumrectangle, then starting new searching areas based on conditions of the smallest angle or acute angle in building TIN.
4. Searching blocks surrounding extending side. After completing an area, it computers new searching blocks based on the biggest angle condition to reduce searching range. When the two confirm to each other, it end the searching.
5. Assigning all areas to no searching flag.
6. Repeating step b to step e until the TIN of the whole area is built.

VI. Algorithm Optimization Analyzing and Assessing
Through the comparisons of the three ways, we can find the third way has high efficiency, relatively simple data structure, so it can be taken as the preferred one. It has been used successfully in "Three Gorges Project Surveying and Mapping Management System". And been proved for the ability of big data quantity processing. On a PC platform (64 M EMS memory, 200MHZ frequency), it takes only dozens of seconds to complete the computations of more than 10,000 points. The high efficiency and superiority of this algorithm in building TIN have been greatly proved.

References

Zhang Zusun, Zhang Jianqing, Principle of Digital Photogrammetry, WuHan Technical University of Surveying and Mapping Press, 1996.