Assessment of Climate-Change Impact on Runoff Using Normalized Difference Vegetation Index

Assessment of Climate-Change Impact on Runoff Using Normalized Difference Vegetation Index

Chi-Chung Lau ¹ , Kwan-Tun Lee ² , Ching-Pin Tung ³ , Chin-Hsin Chang ²
¹ :Laboratories of Energy and Resources, Industrial Technology Research Institute,
Bldg.24, 195-6, Sec.4, Chunghsin Rd., Chutung 310, Taiwan
Tel. (886)-3-591-5469 Fax.(886)-3-582-0038
E-mail: cclau@erl.itri.org.tw
² National Ocean University , ³ National Taiwan University

Abstract
Climate-change influences rainfall-runoff process by changing weather input and basin's characteristics. This study uses remote sensing based vegetation index (NDVI) to evaluate the change of vegetation under 1xCO₂ and 2xCO₂ conditions. Some studies shown that vegetation belt shifts up with temperature on a rate of +180m/1°C. NDVI distribution curve simulates this shift of vegetation, and then calculates new evapotranspiration parameter of a rainfall-runoff model. CCCM, a general circulation model of NCAR, provides monthly precipitation and temperature on 2xCO₂ conditions, and daily data were generated with a first-order Markov chain model. Four basins located on difference water resource regions are processed to calculate flow duration curves (FDC). FDC result indicates that four basins have higher flood flow. Northern and eastern regions have smaller flow rate during drought period but the other two regions have larger values. Mean flow rate (Q₅₀) on southern region in 2xCO₂ is five times then that in 1xCO₂ condition.

Introduction

Basin-scale Modeling
Many satellite remote sensing programs have been launched for studying atmospheric vapor and their land surface relationship. General procedure is developing a series of algorithms that integrate data from remote sensing for simulating Water-Energy-Carbon, Carbon and Biogeochemistry. On the other hand, General Circulation Model (GCM) provides global scale solution of precipitation and temperature while carbo-dioxide concentration rises. Many GCMs have concluded that more precipitation falling in high latitude area and causing more runoff. In low latitude area, runoff is decreased due to less rainfall and higher temperature. Simultaneously increasing precipitation and temperature makes more flood and drought problems. However, water resource engineers do not satisfy the answer because the broad scale is non-suitable for operation purpose. What the engineers needed is a “basin-scale” result. This study present a short cut that develops a basin-scale model simulating runoff under 2xCO₂ condition by combining GCM output and remote sensing data.

Study method
Study procedure is arranged as Fig.1:

Developing a hydrologic model that has hydrologic meaning parameters.
Estimating the relationship between parameter and physiographic factor, remote sensing helps to represent the vegetation condition of watershed and to bridge parameter and climate change.
Generating daily rainfall and temperature data from GCM’s monthly output.
Estimating new vegetation pattern from GCM output on 2xCO₂ condition, and new model parameter from vegetation-parameter relationship.
Combining the results of step 3 and step 4 to simulate runoff and follow up assessment.

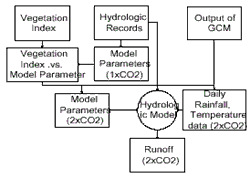
Fig 1. Study Flow Chart
Hydrologic Model

Model Structure
We develop a simplified SWM (Lau, 1996) which has three storage layers simulating fast response (Fig.2), slow response, and ground water of a watershed. Model detail has described in original paper and briefly express as following:

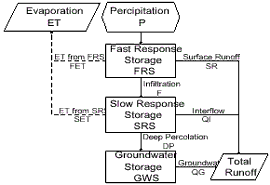
Fig 2.Structure of Hydrologic Model
Fast Response Zone The zone simulates basin’s top depress and top soil layer. While precipitation (P) fall, water stay in the zone that is called Fast Response Zone Storage (FRS). Flow can be represented as:
FRS(t)=P(t)+FRS(t-1)-F(t-1)-SR(t-1)-FET(t-1)………………(1)
In eq. 1, t stands for time period. Surface runoff, SR, is calculated by Manning’s equation controlled by a roughness and slope parameter GEO. FET is assumed a free evaporation that estimated by smaller value between potential evapotranspiration (PET) and FRS. PET can be calculated with Blaney Criddle (1958) method by given average temperature.

Slow Response Zone
Slow response zone emulates lower soil zone. Moisture in the zone is called Slow Response Zone Storage (SRS) that can be formulated as:
SRS(t)= F(t)+SRS(t-1) -QI(t-1)-DP(t-1)-SET(t-1)………………(2)
F is decided by infiltration coefficient A, SRC and water content SRS. QI is calculated by interflow recession constant,KI. SET is determined by a vegetation related coefficient CET and water content SRS. DP is just decided by the ration of water content and zone’s capacity (SRC)s

Ground Water Zone
Ground Water zone Storage (GWS) receives deep percolation (DP) and outlet ground water (QG):
GWS(t)= DP(t)+GWS(t-1) -QG(t-1)……………………………(3)
Estimation of ground water is from recession constant (KG):
QG(t)=(1-KG) GWS(t)…………………………………………(4)
Outlet discharge from basin is the total of SR, QI and QG. There are total five parameters (Table 1) needed to calibrate by fitting estimated and historical discharge, and two recession constants are estimated by recession section of hydrographies. To study correlation between physiographic factor and parameters, remotely sensed data transfer two indexes: vegetation and soil index that makes it possible to bridge parameter and physiographic factor.

Model Calibration
Subjected by officer of Water Resource Bureau, four basins located on different regions, namely Fusan (northern region), Chichawan (middle), Sandiman (southern), and Lisan (eastern), are selected due to their scarcely human-activity. Raingages inside watershed were counted for calculating average daily rainfall. Corresponding temperature and runoff data were put together to calibrate parameters with constrain Rosenbork algorithm. Model parameters are shown on table 1.
Table 1. List of Calibrated Parameters

Parameter	Fusan	Chichiawan	Sandiman	Lisan
Recession constant of interflow, KI	0.827	0.888	0.812	0.828
Groundwater recession constant, KG	0.953	0.971	0.916	0.967
Fast Response Zone Capacity, FRC	263	176	221	163
Slow Response Zone Capacity, SRC	1231	784	756	853
Surface Runoff Coefficient, GEO	4.75	2.6	1.54	1.67
Infiltration coefficient, A	1009	1206	1345	1297
Evaportranspiration coefficient, CET	91	83	76	112

Climate-Change Scenario

Output of General Circulation Model
Usually, assessment of climate-change impact uses scenario on double CO₂ (2xCO₂) concentration condition. There are three ways to composite scenario:

Building forecasting model by analyzing historical data;

Implementing sensitive analysis by changing statistics of historical data;

disaggregating GCM’s monthly output to daily rainfall and temperature data.
Intergovernment Pannel on Climate Change (IPCC) does no suggest the first two approaches because history cannot forecast future in non-linearly complex system. This study adopts output of GCM to estimate 2xCO₂ scenario. Tung (1996) uses output of four major GCMs (CCCM, GFDL, GISS, and UK89) from NCAR to estimate rainfall ratio and temperature difference of Taiwan’s major meteorologic stations. Data were classified into 4 regions, only UK89 show different results in northern and southern regions. GISS show low values in southern stations. Tung suggests that taking output from different grid causes inconformity. For this study, only CCCM provides output at grid 121.9°E 26.3°N (Table 2) and thereby is selected for generating daily data.
Table 2. Weather change ratio from output of CCCM

Month	P_2xCO₂ / P_1xCO₂	T_2xCO₂ - T_1xCO₂	Month	P_2xCO₂ / P_1xCO₂	T_2xCO₂ - T_1xCO₂
January	0.81	2.71	July	1.00	2.09
February	1.05	3.66	August	1.19	1.75
March	0.67	4.73	September	1.40	2.62
April	1.11	4.16	October	1.01	2.45
May	1.13	4.21	November	0.86	2.39
June	1.39	2.52	December	0.66	3.42
			Average		3.05

Synthetic daily precipitation and temperature
Output of GCM provides monthly average data. A Markov chain process is applied to disaggregate them to daily data. The chance of rainfall existence is decided by preceding day’s rainfall and the probability of monthly rainfall (Richardson, 1981). Once rainfall chance is decided, amount of rainfall can be described by one-parameter Weibull distribution (Tung, 1995)
F_xm(x)=1-Exp[-(1.191X/L_m)^0.75 ] ……………………………………(5)
Here L_m is the average rainfall of month-m. Computation starts from generating random number of [0,1] uniform distribution and then calculating F_xm, and rainfall X.

Because only daily average temperature is needed, a first-order Markov-chain model is developed to calculate daily temperature using standard deviation and auto-correlation of monthly temperature:
T_ij=Tavg_i+ACF_i[ T_i,j-1-Tavg_i] +TSD_i+NORM_x(1-ACF_i²)^0.5 …………(6)
Here T_ij is temperature of month I, day J. Tavg_I is average temperature of mouth I, ACF_I is auto-correlation of mouth-i. TSD_I is the standard deviation of temperature of mouth-i. NORMx is normal distribution random number.

Spatial distribution of Vegetation Index

literatures review
Normalized different vegetation index (NDVI) derived by satellite remotely sensed data contributes spatial distribution of biomass. Frieal etl. (1995) believes that NDVI is a major tool to utilize remote sensing in hydrology for deriving model parameter. Ozenda and Borel (1990) found that 1°C rise of temperature causes 180 meters raising of vegetation belt from data of the mountains of Alps. Houerou (1992) found similar trend from Mediterranean data that vegetation zone lifts up 100 meter with temperature rising 0.55°C. He also concluded Mediterranean plant may lifting up 545 meters due to 3°C rising of temperature . Because of lack of similar study in Taiwan, the trend of 180 meter/1°C is adopted in this study to quantify temperature-induced vegetation change.

Relationship between vegetation and hydrologic-model parameters
Landsat 5/TM images acquiesced on January 9, 1995 at 9:33 morning were used. Solar zenith angle of the scene was 58.36 and azimuth was 140.36. Original 30-meter-resolution data are rectified and re-sampled into 25-meter resolution, and were registered to Transverse Mercator (WGS84) projection. Bi-direction reflectance distribution function is used to adjust topographic effect.

Five model-parameters relate to surface roughness, soil infiltration, plant evapotranspiration were counted for their relationship with remote sensing index. After different tries to soil brightness and vegetation indexes, results show that evapotranspiration coefficient (CET) appears better correlation with NDVI (Table.3 and Fig.3).
Table 3. NDVI and CET values of 1xCO₂ and 2xCO₂ conditions

Basin	1 x CO₂		2 x CO₂
Basin	N D V I	CET	N D V I’	CET’
Fusan	0 .4 0 0 2	91	0 .3436	91
Chichiawan	0.3108	83	0.3701	95
Sandiman	0.2215	76	0.3034	85
Lisan	0.4212	112	0.4591	108

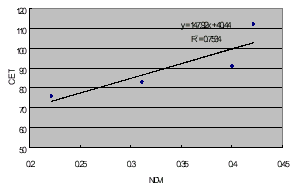
Fig.3 Regression plot of NDVI via CET
NDVI values in Table 3 are average of all pixels inside basins. When running 2xCO₂ scenario, a rising annual temperature (3°C) makes a right shift of NDVI-elevation curve 540 meters (3°C x 180 meter / 1°C) (Fig.4). A new NDVI average is estimated and new CET can be calculated from regression equation (CET = 147.9NDVI+40.44).

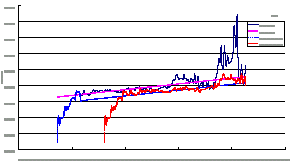
Fig.4 Elevation-NDVI curves of Fusan
Results and discussion
Above computation gives 50-year of synthetic rainfall and temperature data , evapotranspiration coefficient, CET, on 2xCO2 condition, and other model parameters. Daily runoff are simulated to calculate flow-duration-curves (FDC) for assessing the runoff frequencies of both 1xCO₂ and 2xCO₂ conditions. Fig. 5 illustrates the FDCs of Fusan basin. Table 4 and Fig 6 summarize the flow change rates. Results show that frequencies of low flow are decreased in Fusan and Lisan basins. Q₉₀ are down to 57% and 49% of original values. However, high flows, Q₁₀ , are increase to 165% and 187%, respectively. It shows high possibility of appearing a peak flow on flood period..
Table 4. Flow rate changes of two climate conditions (Q_2xCO2 / Q_1xCO2)

Exceed Possibility	Fusan	Chichiawan	Sandiman	Lisan
90%	57%	108%	163%	49%
80%	58%	105%	223%	58%
70%	63%	110%	331%	71%
60%	70%	109%	431%	86%
50%	82%	102%	498%	103%
40%	98%	106%	344%	124%
30%	118%	111%	271%	144%
20%	137%	130%	242%	169%
10%	165%	162%	228%	187%

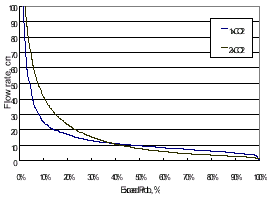
Fig.5 Flow duration curve of Fusan

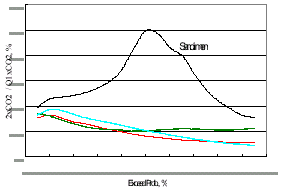
Fig.6 Flow change rate of four basins
Lisan and Sandiman basins have increasing values in both low and high flows. Though Sandiman locates on tropical southern-Taiwan, higher temperature doesn’t evaporate the extra rainfall supply during drought period. Comparing mean flows, Q₅₀, of the four basins, Chichiawan and Lisan show insignificant change. Fusan reduces to 82% of original condition, while Sandiman on the south has five times of original flow. Southern region has very low mean flow on present condition that may cause this significant increase. Table 5 shows the ratio comparing flows of different possibilities from 1xCO₂ and 2xCO₂ conditions. Sandiman shows higher values on Q₅₀/Q₉₀ and Q₁₀/Q₅₀. 2xCO₂ condition introduces increase rate of Q₅₀ that makes an improvement of non-uniform timely distribution on southern region.
Table 5 Ratio of flow of different exceed possibilities of the four studied basins

Flow Ratio	Fusan		Chichiawan		Sandiman		Lisan
Flow Ratio	1 xCO₂	2 xCO₂	1 xCO₂	2 xCO₂	1 xCO₂	2 xCO₂	1 xCO₂	2 xCO₂
Q₅₀/Q₉₀	1.90	2.72	2.56	2.41	3.46	10.54	1.72	3.59
Q₁₀/Q₅₀	2.57	5.20	3.43	5.46	27.29	12.49	3.30	6.00

Conclusion
The study combines rainfall-runoff model, vegetation index defined by remote sensing, output of GCM , and data disaggreation model to estimate the changed evapotranspiration parameter for calculating runoff of four basins located on north, middle, south, and east regions. Flow duration curves is calculated to assess the impact of runoff from climate change. Results show that:

Fusan (north region) and Lisan (east region) show larger flood and smaller drought flow. Increasing rainfall and warmer weather brings double impact to the two basins. Chichiawan (middle region) shows insignificant changes on flood but smaller drought flow.
Sandiman (south region) has significant increase flow rate at all exceeded probabilities. A five-time high of average flow provides positive contribution for water resource planning.
High flow, Q₁₀, are increase in all four basins, and the Sandiman basin makes a highest value of 228% that makes negative impact on flood control.

Reference

Hun, Lan-Min, Chin-Pin Tung, "Affection of Climate-Change to Taiwan’s Hydrology,” Proceeding, Conference of Agricultural Engineering, Taipei, pp.683-690(1996).
Houerou, H. N. Le, “Vegetation and Land-Use in the Mediterranean Basin by the Year 2050: A Prosectire Study” in Climate Change and the Mediterranean (L. Jeftic Edited), Edward Arnold, London, pp.175~232. (1992).
Lau, Chi-Chung, ”Assessment of Climate-Change Impact on Hydrologic System of Taiwan using Remote Sensing (I),”, ERL/ITRI report 06-3-85-0176, Hsinchu (1995).
Shoshany, M., P. Kutiel, H. Lavee and M. Eichler, “Remote Sensing of Vegetation Cover along a Climatological Gradient,” ISPRS. Journal of Photogrametry and Remote Sensing, Vol.49,No.4,pp.2-10(1994).
Skiles, J. W. and J. D. Hanson, “Responses of Arid and Semiarid Watersheds to increasing Carbon Diexide and Climate Change as Shown by Simulations Studies,” Climate Change, Vol.26, pp.377-397,(1994).
Tung, Chin-Pin, Douglas A.Haith.”Weather-form Classification and Precipitation Simulation Model,” Proceeding, Conference of Agricultural Engineering, Taipei, pp.167-182(1995).