Preliminary Studies for Estimating Surface Soil Moisture and Roughness Based on a Simultaneous Experiment with CRL/NASDA Airbone SAR (PI-SAR)

Preliminary Studies for Estimating Surface Soil Moisture and Roughness Based on a Simultaneous Experiment with CRL/NASDA Airbone SAR (PI-SAR)

Takeo Tadono , Muhtar Qong , Hiroyuki Wakabayashi, Masanobu Shimada,
Research Fellow, Earth Observation Research Center,
National Space Development Agency of Japan
1-9-9, Roppongi, Minato-ku, Tokyo 106-0032 JAPAN
Tel: (81)-3-3224-7113, Fax: (81)-3-3224-7052
E-mail: tadono@eorc.nasda.go.jp
Tatsuharu Kobayashi,
Communications Research Laboratory
4-2-1, Nukui-kitamachi, Koganei, Tokyo 184-8795 JAPAN
and Jiancheng Shi
Institute for Computational Earth System Science,
University of California, Santa Barbara, CA 93106 USA

Keywords: Soil moisture, Surface roughness, Numerical simulation, Polarimetry, SAR

Abstract
The goal of this study is to estimate the surface soil moisture and surface roughness using polarimetric Synthetic Aperture Radar (SAR) data. In this study, a preliminary analysis for approaching this objective was conducted based on a sensitivity analysis of surface parameters. A numerical scattering model was used, and the results were compared using only like-polarized backscattering coefficients obtained from the data of an experiment conducted simultaneously with an airborne SAR. The surface correlation function was considered in this analysis. Because the problem is site-specific, and depends upon the measurement accuracy of both the ground truth data and the SAR system including speckle noise, as well as the model uncertainty, the comparison results did not agree well with measured and inferred values of both the soil moisture and surface roughness. In particular, the moisture was underestimated and the roughness was overestimated.

Introduction
Monitoring spatial and temporal changes of soil moisture is very important to numerous environmental studies, including hydrology, meteorology, and their interactive fields. In spite of its importance, soil moisture is not generally used for weather forecasting and water resources management because it is difficult to measure on a routine basis over large areas. However, recent advances in microwave remote sensing have demonstrated the potential to measure soil moisture quantitatively on bare and short-vegetated surfaces (Engman and Chauhan, 1995). In attempting to use active microwave remote sensors to estimate this important parameter, several algorithms have been developed by using Synthetic Aperture Radar (SAR) image data. The signal returned to SAR is known as the backscattering coefficient (s ⁰_qp; where subscript p is the transmitting polarization state and q is the receiving polarization state), which is affected by not only dielectric properties that depend on the soil moisture, but also on surface roughness, correlation length and other surface characteristics. Previous studies (Wang et al., 1986) have revealed that Shuttle Imaging Radar-B (SIR-B) imagery with a single frequency and single polarization system can only describe the dependence of backscattering coefficients on these surface parameters. Tadono et al. (1999) developed an algorithm including some assumptions based on hydrological knowledge, and estimated the soil moisture distribution using two seasonal Japanese Earth Resources Satellite-1 (JERS-1) SAR images.

Radar backscatter studies became more rigorous with the availability of polarimetric radar data and more sophisticated algorithms for estimating soil moisture were presented. Oh et al. (1992) developed an empirical model to estimate the root mean square (rms) roughness height and soil moisture from the co-polarized ratio (s ⁰_hh/s ⁰_vv ; where subscripts h and v are horizontal and vertical polarizations), and the cross-polarized ratio (s ⁰_hh/s ⁰_vv) over bare soils of different roughness and moisture conditions was measured by a truck-mounted scatterometer system. Also, Dubois et al. (1995) developed a model that only requires measurements of s ⁰_hh and s ⁰_vv at frequencies from 1.5 and 11GHz to retrieve both rms roughness height and soil moisture from bare soil and applied to the L-band data acquired by both the Airborne SAR (AIRSAR) and Shuttle Imaging Radar-C (SIR-C) over a test site in Oklahoma, USA. Hajnsek et al. (1999) applied the above two empirical models to L-band data of the airborne Experimental SAR (E-SAR), and compared the performance and accuracy of estimated values. They found that the valid pixels of the E-SAR data decrease to less than 56% of the total number of pixels. Furthermore, soil moisture was underestimated and roughness was overestimated for both models because the regression fits necessary to estimate the roughness and moisture were dependent on the used data sets. Shi et al. (1997) pointed out that neither of the above empirical models considered the surface power spectrum. In addition, these empirical models developed from a limited number of observations might have site-specific problems due to nonlinear responses of backscattering to the soil moisture and surface roughness parameters. Therefore, an algorithm based on the single-scattering Integral Equation Method (IEM) was developed to estimate soil moisture and surface roughness from dual-polarized SAR measurements and subsequently applied to both L-band AIRSAR and SIR-C data. Consequently, the rms errors of comparison were found to be 3.4% for moisture and 1.9dB for roughness.

The objective of this study is to consider the preliminary examination to estimate the surface soil moisture and the roughness by using polarimetric SAR data. A numerical model was used to analyze the sensitivity of surface parameters and to estimate the moisture and roughness using data from an experiment conducted simultaneously with a multi-parameter airborne SAR that has a dual-frequency (L- and X-bands) and quadruple polarization and is called “PI-SAR” (Polarimetric and Interferometric SAR) (Wakabayashi et al., 1999).

Scattering Model And Sensitivity Analysis
The scattering model used in this study formulates scattering processes from an inhomogeneous medium composed of irregular soil particles and water. The model consists of terms for surface and volume scattering. The surface scattering from the air-soil interface (soil surface) is calculated by the single-scattering IEM model (Fung, 1994), which is valid for a wider range of surface roughness conditions than the other classical model (Ulaby et al., 1986). The IEM model is needed to evaluate the surface correlation function in the general form of
p(x)=exp[x/I)ⁿ] (1)
where l is the correlation length of the surface roughness. The general form is an exponential function when 1 =n and becomes a Gaussian function when 2 =n . The volume scattering within the medium is calculated based on the first-order radiative transfer solution (Fung, 1994; Shi and Dozier, 1995). Furthermore, the semi-empirical model for a four-component mixture (Dobson et al., 1985) is used to convert the volumetric soil moisture ( Mv) to the dielectric constant (e_r ), assuming typical sandy soil in this study.

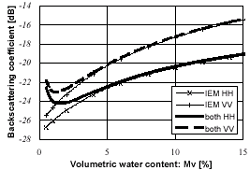
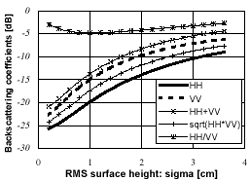
When the soil moisture is high, the total backscattering will be due primarily to the surface scattering because the reflectivity at the surface is significantly more and less power is transmitted across the air-soil interface. However, the volume scattering can not be neglected under nearly perfectly dry conditions. Figure 1 compares two cases of calculating the backscattering coefficients (s ⁰_hh and s⁰_vv), one considering only surface scattering (the polarizations of HH and VV are represented by the symbols x and +) and the other considering both surface and volume scattering (solid and dotted curves), as a function of Mv at an incidence angle (q_s) of 40 degree, an rms surface height (s) of 1.4cm, =l 15cm, and the exponential correlation function are assumed. If the soil moisture content is under 2%, the differences between the two cases of calculating backscatter for both polarizations exceed 1 dB. Figures 2 to 4 show results of the sensitivity analysis for all polarization states of the model evaluated for both surface and volume scattering at 1.27 GHz (L-band), q_s= 40 degree, and an assumed exponential correlation function as a function of Mv (Fig. 2),s (Fig. 3), and l (Fig. 4). It will help to select polarization measurements that are most sensitive to each parameter. The backscattering coefficients (in dB) are plotted for s ⁰_hh (solid curve), s ⁰_vv (dotted curve), s⁰_hh+s ⁰_vv (x),

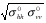(+), and s ⁰_hh/s ⁰_vv (*). Figure 2 clearly shows that the dependence of s⁰_hh and s⁰_vv on Mv is nonlinear. For example, s⁰_hh increases about 8.2dB as Mv varies from 2 to 50% as compared to 12.1dB for s ⁰_vv , 10.9dB for s⁰_hh + s ⁰_vv, 10.1dB for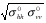

, and 3.9 dB for s⁰_hh/s⁰_vv . Also, s⁰_hh reaches saturation faster than the other polarization states. To simulate dependence of backscattering on s , Fig. 3 assumes wet soil ( Mv= 30%) and l = 15cm. In the figure, s⁰_hh increases about 16.8dB as s varies from 0.2 to 3.6cm as compared to 16.4dB for s⁰_vv , 16.5dB for s⁰_hh+s⁰_vv and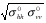

, and 2.1 dB for s⁰_hh/s⁰_vv. Furthermore, the curve shapes are similar to those in Fig. 2 for each polarization state. From Fig. 4 (s = 1.4cm; Mv= 30%), the sensitive of l is less to backscatter than other parameters (i.e., Mv and s ).s⁰_hh/s⁰_vv increases about 1 dB from 2.5 to 20 cm as compared to about 3 dB for others.


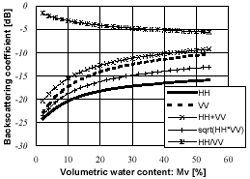Figure 1. Effect of volume scattering on soil moisture variation at 1.27GHz, 40 degree incidence angle. An exponential surface correlation with s=1.4cm and l =15cm was used. Symbols x and + represent surface scattering, the solid and dotted lines represent surface and volume scattering.	Figure 2. Numerical simulation of backscattering dependence on soil moisture by polarization states. The solid, dotted, x, + , and * are for s ⁰_hh,s ⁰_vv, s ⁰_hh+s ⁰_vv,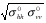,s ⁰_hh/s ⁰_vv, respectively. Input parameters were the same as in Fig. 1.


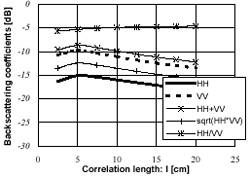Figure 3. Simulated backscattering dependence on rms surface height at the Mv =30%. Other parameters were the same as in Fig. 1.	Figure 4. Simulated backscattering dependence on correlation length at s =1.4cm. Other parameters were the same as in Fig. 3.

Comparison With Field Experiment

Simultaneous Experiment
A simultaneous experiment with PI-SAR was conducted on July 14, 1999. However, the selected day was not good for validating the surface soil moisture because it rained very much. Three test sites with bare land or short vegetation were selected to validate the soil moisture and roughness. Two test sites were located in the “Tomakomai Experiment Forest” of Hokkaido University, Japan (see Qong et al., 1999), which is a very flat forest area and very well maintained. The surface soil moisture was obtained by the Time-Domain Reflectometry (TDR) method and direct sampling method; the horizontal profiles of the land surface height were measured by comb-style instruments (80cm length, 2mm interval) to evaluate the surface roughness parameters (i.e., s , l , and surface correlation function). The ground truth data of one test site in the felling forest area was used in this study.

Evaluation of Surface Roughness Parameters and Correlation Function
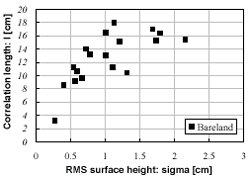
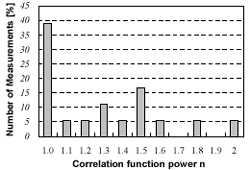
A total number of 18 surface roughness profiles were obtained in one test site (two profiles for each measured point). s and l were calculated from these data (Ulaby et al., 1986), and the results are shown in Fig. 5. To find the surface correlation function, eq. (1) was fitted to the measured autocorrelation from the measured roughness profiles for various values of n . Figure 6 shows an example of the measured auto correlation compared with the exponential and Gaussian correlation functions; the results are summarized in Fig. 7 where the number of occurrences was plotted as a function of the power n (Shi et al., 1997). Figure 7 indicates that about 67% of the measured roughness profiles at this test site can be described by exponential correlation functions with n£1.4.

Comparison of Measured and Calculated Backscattering Coefficients
Figure 8 compares s⁰_hh and s⁰_vv obtained by PI-SAR and calculated by the model with measured Mv, s , l , and 1 =n input for the test site. Besides roughness measurements, Mv was sampled three times by TDR at one point, then calibrated and averaged for each point. Figure 8 indicates that some of the calculated backscattering coefficients were in good agreement with measured ones. However, calculated s⁰_hh values were almost always underestimated.


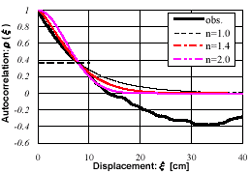Figure 5. Relationship between measured s and l at the test site.	Figure 6. Example of comparisons between measured autocorrelation (solid curve) and general correlation with n=1.0, 1.4, 2.0 (dotted curves).


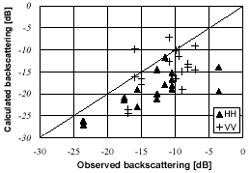Figure 7. Summary of the result of fitting the surface correlation function to measured autocorrelation.	Figure 8. Comparisons between backscattering coefficients observed by PI-SAR and calculated using measured parameters, Mv , s and l . The data points for s⁰_hh and s⁰_vv are represented by the symbols and +, respectively.

Simple Algorithm for Estimating Moisture and Roughness
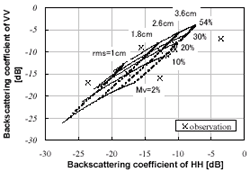
A simple algorithm is used to estimate the soil moisture and surface rms height simultaneously from polarimetric SAR data, employing only s⁰_hh and s⁰_vv and assuming l . Figure 9 shows an example of the inversion diagram at 1.27GHz, 38.9 degree incidence angle corresponding to the test site, l = 15 cm, and exponential correlation function. The variations of Mv and sare represented by the solid and dotted curves, respectively, and the measured values, by x. If the measured value is plotted in the simulated range, Mv and s for each pixel can be inferred from Fig. 9. However, it is difficult to consider all pixels, and only five pixels can be used in this case. Figure 10 summarizes the inferred results for Mv. Figure 10 indicates that the soil moisture is underestimated. Also, the inferred s is overestimated, which is the same as the trends of Hajnsek et al. (1999).


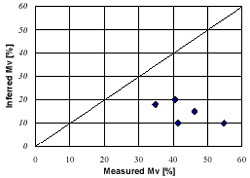Figure 9. Inversion diagram using s⁰_hh and s⁰_vv at l=15cm. The solid curves show variations of Mv; the dotted curves, the variation of s; and the symbol x, observed by PI-SAR at the test site.	Figure 10. Comparisons between the inferred and ground measured soil moisture for the test site. Only five pixels at the test site could be calculated.

Conclusions
This study sought to infer the surface soil moisture and roughness based on a sensitivity analysis performed using a scattering model including the surface correlation function, then to compare the results with data from a simultaneous PI-SAR experiment. Because the problem is site- specific, the measurement accuracy of both the ground truth data and the SAR system, including speckle noise, is not optimum, and the model has uncertainty, measured and inferred values of the soil moisture and surface roughness did not agree well. It is thus necessary to examine the algorithms to estimate the soil moisture based on the radiative transfer solutions.

Acknowledgements
The authors would like to thank Prof. Hiura and Mr. Okuyama of Hokkaido University for implementing the field experiment, and their CRL colleagues and Mr. Kawada of RESTEC for processing the PI-SAR data.

References

Dobson, M. C. et al., 1985. Microwave dielectric behavior of wet soil, Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sensing, GE-23, pp.35-46.
Dubois, P. C. et al., 1995. Measuring soil moisture with imaging radar. IEEE Trans. Geosci. Remote Sensing, 33, pp.915-926.
Engman, E. T., and N. Chauhan, 1995. Status of microwave soil moisture measurements with remote sensing. Remote Sensing Environ., 51 (1), pp.189-198.
Fung, A. K., 1994. Microwave Scattering and Emission Models and Their Applications, Norwood, MA: Artech House.
Hajnsek, I. et al., 1999. Determination of hydrological parameters using Airborne-Radar data (DLR E-SAR). IEEE IGARSS ’99 Proceedings, pp.1108-1110.
Oh, Y. et al., 1992. An empirical model and inversion technique for radar scattering from bare soil surface. IEEE Trans. Geosci. Remote Sensing, 30, pp.370-378.
Qong, M. et al., 1999. Land Cover Classification Using CRL/NASDA PI-SAR Data, The 20 th Asian Conference on Remote Sensing proceedings (being submitted).
Shi, J., and J. Dozier, 1995. Inferring snow wetness using C-band data from SIR-C’s polarimetric Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sensing, 33, pp.905-914.
Shi, J. et al., 1997. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sensing, 35, pp.1254-1265.
Tadono, T. et al., 1999. Development of a SAR algorithm for soil moisture mapping in permafrost regions including the effect of surface roughness. JSCE Jornal of Hydroscience and Hydraulic Engineering (being submitted).
Ulaby, F. T. et al., 1986. Microwave Remote Sensing, Active and Passive, MA: Artech House. Wakabayashi, H. et al., 1999. Airborne L-band SAR system: Characteristics and initial calibration results. IEEE IGARSS ’99 Proceedings, pp.464-466.
Wang, J. R. et al., 1986. The SIR-B observations of microwave dependence on soil moisture, surface roughness, and vegetation covers. IEEE Trans. Geosci. Remote Sensing, 24, pp.510-516.