GISdevelopment.net ---> AARS ---> ACRS 2000 ---> Digital Photogrammetry An Iterative Approach to Acquire Linear Features under the constraints of their knowledge in Object Space Shih-Hong CHIO and Shue-Chia WANG Ph.D. Candidate and Professor Department of Surveying Engineering, National Cheng-Kung University No. 1, University Road, Tainan, TAIWAN Tel:(+886)-6-2373876 ext.834; Fax:(+886)-6-2375764 E-mail: p6883102@sparc1.cc.ncku.edu.tw Key Words Geometric constraint, Matching, Linking, Object knowledge Abstract 3-D linear segments are crucial primitives for reconstruction of man-made buildings. This paper presents one iterative approach to acquire more linear segments from stereo image pair with known orientations under the constraints of their knowledge in object space. The major algorithm in this iterative approach is referred as "Core Algorithm" which simultaneously match and link linear segments based on their knowledge in object space. This iterative approach consists of four processing procedures. No additional height constraint is used in the first processing procedure. The other three iterative processing procedures will employ average height from relevant 3-D linear segments as additional height constraint to acquire more 3-D linear segments by using Core Algorithm. We hope this iterative approach will increase the amount of the acquisition of 3-D linear segments. 1. Introduction 3-D linear segments are crucial primitives that constitute most of the man-made objects, especially the roof boundaries in the aerial images. Therefore, they are very important for the reconstruction of man-made object. No matter what kind of method is used to acquire those 3-D linear segments, i.e. segment stereo-matching algorithm in [1], it is impossible to obtain all the 3-D linear features. Therefore, this paper would like to presents one iterative approach to acquire more 3-D linear segments under the constraints of their knowledge in object space. The core algorithm of this iterative approach is to simultaneously match and link the linear segments based on their knowledge in object space. Firstly, Core Algorithm is used to those linear segments according to the order of their geometric structure. No additional height constraint from adjacent 3-D linear segments could be imposed in this step. During this first process, when it succeeds, the average height of this acquired 3-D linear segment will be immediately introduced as additional constraint to handle the adjacent linear segments of this successfully processed linear structure by Core Algorithm. This is the second iterative process. Subsequently the same Core Algorithm with height constraint are used in the third iterative process to handle the remaining linear segments that are the members of the successfully processed linear structure. Finally, Core Algorithm together with height constraint will be once more applied to those remaining linear segments that locate at the certain range of those already successfully processed linear segments. We will describe Core Algorithm in Section 2 and this iterative approach in Section 3. The relevant experiments will be shown in Section 4. Finally, short conclusions will be drawn in Section 5. 2. Core Algorithm for Matching and Linking in Object Space 2.1 Available Knowledge of 3-D Linear Segments in Object Space and Their Calculations As stated before, Core Algorithm will match and link linear segments based on their object knowledge. Hence, this section will describe the relevant knowledge of 3-D linear segments and their calculations. We assume that man-made 3-D linear segments should be either oblique or horizontal. Since they are man-made, their change rate of height in object space should be reasonable. For one horizontal 3-D linear segment, the real change rate of height should be close to zero meter per meter (short for m/m). For one oblique 3-D linear segment, the real change rate of height along this line should be constant and within a reasonable limit. These two definitions for change rate of height are the main knowledge of linear segments in object space that will be used as constraints in our method to match and link linear segments. Also, it implies that several linear segments with same change rate of height could be the same one. Of course, if this 3-D linear feature is horizontal, then the same height information will be its another knowledge. Next we will explain how to calculate the change rate of height of one 3-D line. 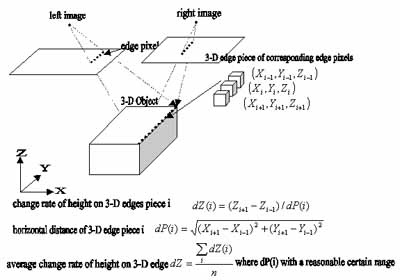Fig.1: Illustration of calculation of the average change rate of height In Fig.1, one 3-D horizontal linear segment is projected onto stereo images. One 3-D edge piece is defined as every three corresponding edge pixel in series and one 3-D linear segment could be regarded as the composition of several 3-D edge pieces. Each corresponding edge pixel will determine its 3-D coordinate in object space by the space intersection, therefore, the ground coordinates on each 3-D edge piece will be known also; then the individual information on each 3-D edge piece will be calculated accordingly (see Fig. 1). Next the object knowledge, i.e. average change rate of height, for each 3-D linear segment will be determined according to those 3-D edge pieces. Now, the details to calculate will be described below. Firstly, the horizontal distance (dP(i)) of 3-D edge pieces i will be defined as shown in Fig.1. It should be limited in terms of pixel resolution and image scale. The limitation of dP(i) corresponds to filter the problematic and unreliable individual change rate of height dZ(i) along this 3-D linear segment. Those unreliable dZ(i) might be caused by noise or by uncertainty of edge points during the edge detection. After the unreliable edge pieces are filtered, average change rate of height dZ of this 3-D linear segment will be determined by averaging dZ(i) from all reliable 3-D edge pieces (c.f Fig.1). Fig.1 just illustrates how to get the knowledge of horizontal line segments, but it's applicable to oblique 3-D line segment. 2.2 Data Preparation At the beginning, Poly-Morphic feature extraction method [2], will be used in this research to extract relevant junctions and edge pixels in image space. After using non-optima suppression to them, one simple edge-linking algorithm is used to link the adjacent pixels together to form longer edges by considering the pixel connectivity. Since 3-D linear features are our concerns and they should be straight lines in image space. Therefore, Douglas-Peucker algorithm [3] is applied to get 2-D linear segments by considering the pixel collinearity. In this research, each pixel coordinate on 2-D linear segments should be recorded in order to calculate their knowledge in object space. Therefore, the major purpose of Douglas-Peucker algorithm is not for the data generation or reduction. For deciding the checking priority of those 2-D linear segments, the feature aggregates, including line structures and junction structures, consisting of junctions and line segments are grouped from geometric proximity and collinearity according to their potential to form man-made buildings. For example, a longer linear segment with junctions near both its endpoints could be more possibility from a roof than a single line segment without anything attached to its endpoints. For our method, the former one should have higher priority to be chosen for processing. More details about the classification of feature aggregates was described in [4]. Then both line structures and junction structures together with flanking attributes, i.e. average gray value, on both sides of linear segments are used to develop this iterative approach to match and link linear segments by considering their knowledge in object space. 2.3 Initial screening of possible candidates This iterative approach will start from higher priority of line structure and is done along the epipolar direction. Since at the beginning we don't know anything about the object knowledge of any linear segment, for each one in left image probably there are many candidates waiting to be chosen in right image. To demand the correctness of results as possible as it can, it is important to give strong constraints for the initial screening of possible candidates in right image. Therefore, object knowledge, geometric and radiometric properties are all considered simultaneously as follows: From geometric consideration: the initial correspondence of the linear segments between the stereo images must have the junction point along the epipolar direction. This factor is only considered in the first iterative processing procedure. The subsequent three iterative processes don't take this into account. Instead, this part will be replaced by the constraint of height. Plus, their absolute difference of azimuth between the correspondence is within one threshold. From radiometric consideration: at least one side of the corresponding flanking regions on possible corresponding 2-D linear segments should have similar gray values, i.e. the difference of their mean gray values should be less than a given threshold. From the object-knowledge consideration: Besides the constraint of the change rate of height, the number of reliable 3-D edge pieces should be higher than one threshold. It implies the length of this 3-D line should be long enough in object space. The standard deviation of average change rate of height is smallest among the candidates and less than one threshold. This criterion demands more accurate change rate of height. 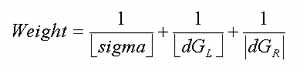Finally, the optimal decision is decided by simple weighting equation: Where sigma: the sigma of height change rate; dGL , dGR: gray difference on the left and right side of line 2.4 Subsequent matching and linking process After finding the initial correspondence, the process will proceed by matching and linking the next linear segments according to the status of Fig.2. From possible liking candidates. The following constraints in object space will be considered for the optimal liking linear segment. For length, the number of reliable 3-D edge pieces should be higher than one threshold. For "man-made" 3-D line, the average change rate of height should be within one certain range. For the "same" man-made 3-D linear feature, the absolute value of difference of average change rate on height between linking linear segment and the initial linked linear segment is the smallest among possible candidates and less than one threshold. The subsequent process proceeds as follows. First, the process will be conducted between the longer linked line segment and the neighboring linear segments of shorter linked linear segments, see Fig.2A and 2B, by the above-mentioned constraints of object knowledge. If the neighboring linear segments could not be found or meet the conditions, the search area formed by the maximum and minimum parallax will be setup. Then the linear segments in this search area, shadow area in Fig 2a and 2b, will be processed under the same constraints of object knowledge. If the linear segments have the same length, as shown Fig.2C and 2c, only the situation in Fig.2C is processed. The process will repeat over and over until no linear segment could be found and linked. From the constraint on the change rate of height, the process would be applied to handle not only the horizontal lines but also the oblique lines. 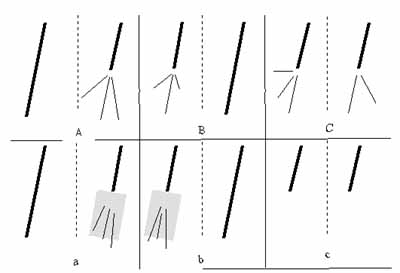Left part means left image and right part shows right image. Thick and Thin lines: already linked and non-linked 2-D lines Fig.2: Possible six situations during linking process by using the stereo images based on object knowledge 3.Iterative Approach to Simultaneously Match and Link the Linear Segments In the iterative approach, Core Algorithm mentioned above is used in each procedure. The iterative processing algorithm is proceeding as follows: Firstly, this iterative approach will begin from the strongest structures to weaker structure in left image, The strongest structures mean their high possibility to correspond with the imaging of roof boundaries in image space. For example, line structure A in Fig.3 has stronger structure than B ,C and D. That is C and D has the weaker structure in this case. If the first iterative process succeeds, then not only the object knowledge of 3-D linear segment but also the average height of this 3-D linear segment will be simultaneously introduced as the constraints in the second iterative process. Besides the additional height constraint, the second iterative process still uses the core algorithm to match and link the linear segments which are the members of this strongest linear structure. The first and second iterative processing procedure will be applied to the linear segments whose structures are from strongest to weakest. Subsequently the third iterative process is applied to the remaining linear segments that are the members of the successfully processed linear structure. The same Core Algorithm will be also utilized and height constraint is also considered in this step. This process proceeds repeatedly until the remaining linear segments don't meet the requirement. Finally, Core Algorithm together with height constraint will be employed to those remaining linear segments that locate in the certain range of those already successfully processed linear segments repeatedly until no linear segment meets the above requirements. Therefore, this iterative approach consists of four steps with one core algorithm and one additional height constraint. The geometric constraint in these four steps becomes less and less and the height constraint is also looser and looser. However, the relevant constraint of object knowledge about 3-D linear segments in Core Algorithm is always unchanged no matter which step it uses. 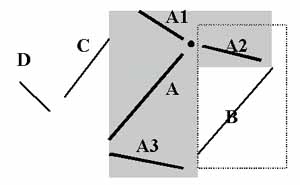Fig.3: the diagram of iterative approach Now take the Fig.3 as an example. The further iterative approach will start from the stronger structure A which consists of one junction and three neighboring linear segments A1, A2 and A3. If the process succeeds, then A1, A2, and A3 will be processed at once. In this case, linear segments A2 is also the neighboring linear segment of the weaker structure B. It is assumed that the process didn't succeed in handling linear segment B due to fail in finding the corresponding junction in right image. The iterative process will process it again in the third step because linear segment B is the adjacent linear segment of linear segment A2, which has been successfully processed. Next, linear segment C is close enough to successfully processed linear segment A1, the process will be initialized again. If the linear segment C also is successfully handled, then the linear segment D is also processed again due to the same reason. Otherwise, all the process will stop. Apparently if only the first iterative processing is applied, it might be impossible to obtain the results from linear segment B, C, and D . Because the result is feedback to restrict and guide another process once more to handling others, therefore, it is possible to produce more results. From the above discussion, the iterative approach does increase the amount of successfully matching and linking the linear segments. Next section will give some experiments. 4.Experiments and Results This section will describe the results of the experiments. The pixel resolution of image pair is 30µm; image scale is about 1:8,000; and their image size is 180*180 and 180*225, respectively. The associated thresholds for Core Algorithm in object space are described as follows: The reasonable horizontal distance of 3-D edge piece (dP(i)) is set as 0.12m. Beside the threshold for the absolute value of average change rate of height is chosen as 1 m/m, the relevant thresholds are set as: In the initial screening of possible candidates, 10 degrees for the azimuth difference threshold and 20 gray values for the difference of mean gray values of the flanking mate. Plus, 8 for the number of reliable 3-D edge pieces and 3m/m for the standard deviation of average change rate of height. In subsequent matching and linking process, 5 for the number of reliable 3-D edge pieces.0.2 m/m for the difference of average change rate of height between candidates and the initial linked linear segment. Fig.4: The result of matching and linking in object space according to their geometric priority Fig.5: The result of matching and linking in object space via further iterative process: height difference 0.5 m The result in Fig.4 is acquired only by the first processing procedure of iterative approach. Only 7 linear segments are successfully acquired. Some line segments could not be successfully processed because the geometrical structure can't meet the requirement of initial screening. However, after the concept of iterative approach is used, the results in Fig.5 show that 11 line segments are acquired. Additional 6 linear segments are obtained. The height difference in third and fourth process is set as 0.5m in the test of Fig.5. If the constraint of height difference is relaxing to 5m, two more will be successfully acquired, not shown here due to short space. Therefore, it could say that the concept of iterative approach could be helpful to get more 3-D linear segments. The results prove this concept could be applicable. Only one correspondence seems questionable, indicated by linear segment a at the upper left in Fig.5. This case is often happened in the urban images of Taiwan area due to the structures themselves. 5.Conclusions From the experiment, this iterative approach does increase the number of matched and linked line segments for the next task. Nevertheless the simple weighting criterion is worthwhile to further investigation. Anyway, the increasing amount will be helpful for the subsequent relevant tasks. References F. Bignone, "Segment Stereo-Matching and Coplanar Grouping", Technical Report BIWI-TR-165, Institute of communication Technology, Image Science Lab, ETH, Zurich, Switzerland, 1995. W. Foerstner, "Framework for Low Level Feature Extraction," in Computer Vision, ECCV '94, vol. II, Lecture Notes in Computer Science, 801, pp. 383-394, J.O. Eklundh, Eds., Springer-Verlag, Berlin, 1994. D. H. Douglaus and T. K. Peucker, "Algorithms for the reduction of the number of points required to represent a digitized line or its caricature," Canadian Cartographer, vol. 10, pp.110-122, 1973. S. H. Chio, S. C. Wang, and B. Wrobel, "A Semi-Automatic System for the Reconstruction of Building Roofs in Dense Urban Areas Using Aerial Stereo Image Pairs," AVN ALLGEMEINE VERMESSUNGS-NACHRICHTEN, pp.167-174, 1999.