GISdevelopment.net ---> AARS ---> ACRS 2000 ---> Educational & Profession

Determination Of Original Size Of The Abhayagiriya Stupa

Siri Diyupathi Dampegama
Senior Lecturer / Superintendent of Surveys
Institute of Surveying & Mapping.
Tele: +94-57-23015 Fax: +94-57-22004
Sri Lanka.
E-mail:ism_surv@sri.lanka.net


Key Words: Size of Stupa, Least Squares

Abstract:
This paper presents an approach developed to determine the original size of the ruined Abhayagiriya stupa built between 89 to 77 BC. Determination of the radius and the centre of the stupa was computed using the mixed model observation equations of general least square principle. The radius of the stupa was determined by taking the coordinates of the old plasters available on the outer surface of the dome. Observations were taken with respect to a three dimensional cartesian coordinate system. Measurements were taken by precise Electromagnetic Distance Measuring (EDM) equipment and the coordinate controls were made by Global Positioning System (GPS). Radius and the centre of the stupa were computed to an accuracy of ±5cm due to the advance technology utilized in field procedure and the computation methodology. The centre of the spire (Koth Kerella) was also determined using the same technology. The shape to be determined by best fitting curve to the old plaster / bricks existing on the stupa.

Introduction
Abhayagiriya stupa was erected by King Valagambahu between years 89 to 77 BC. This is one of the largest religious structure of the world during its construction period. The Abahayagiriya stupa was situated at the city of Anuradhapura in the north central province of Sri Lanka.The initial stupa built by king Valagambahu was much smaller than the present monument and no records were available about its initial dimension. But it was considerably enlarged by successive kings such as king Gajabahu I who has restored guard houses at the four entrances between years 112-134 AD. At present the outer surface of the dome is completely deteriorated due to weathering. But several small patches of original outer plaster are existing in the dome and preserved by the Archeological Department and Central Cultural Fund.

The following procedure was adopted in order to determine the radius of the stupa using the available remaining plaster and bricks of the original stupa.

Procedure
After careful investigation of the stupa it was decided to obtain rectangular cartesian coordinates of all points connected to the new conformal grid coordinate system used by the Sri Lanka Survey Department. Control stations were established using precise Global Positioning System. This was done by four LEICA SR 399 geodetic type GPS receivers. Eight control stations were established around the stupa using above technique. In addition to the GPS control stations seven additional control points were established using Electro Magnetic Distance Measuring technology (EDM). A SOKKIA SET 3B digital total station was used in order to pick up the coordinate of the dome plaster and the points identified as on original structure of the stupa. Six circles at the base of the stupa were identified in order to compute the radius and the coordinates of the centre of the stupa as follows.
  1. Circle constructed by stones on the stone paved terrace around the base of the stupa. (Salapathala Maluwa)
  2. Circle formed by the stone basement of the lower Pesawa. (Welikonda.)
  3. Circle formed by the top of first Pesawa.
  4. Circle formed by the top of second Pesawa.
  5. Circle formed by the top of third Pesawa.
  6. All existing old plaster patches of the lower part of the dome.

Another five circles formed by undisturbed old work on the spire (Koth Kerella) were also identified to compute the centre at the top of the stupa in order to check the verticality.

Coordinates of all points identified as original construction were picked up by SOKKIA SET 3B total station to the accuracy of ± (5mm + 3ppm.). This instrument is capable of storing the coordinates digitally and the coordinates were down loaded to a computer for post processing.



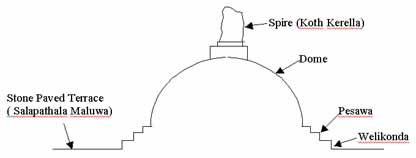
Diagram 1. Cross Section of Stupa. Mathematical Model


The observed points are on concentric circles with their centres at the centre of the stupa. The mathematical equation of the circle (equation 1 below) was taken as the model to construct observation equations.

x2 + y2 - 2gx - 2fy + C = 0 (1)

The radius of the circle is given by,

r = (g2 + f2 - C )1/2 (2 )

where,
g = North coordinate of the centre
f = East coordinate of the centre

According to equation (1) above, parameters g, f & C could be computed if coordinates of three points on the circumference of the circle are known. When more than three points are available on the circle, the best fitting circle which passing through the points can be obtain by the least square adjustment. As the coordinates are also contaminated by random errors the general least square solution with mixed observation equation model was selected to compute the parameters of best fitting circle.

The number of points available on the circumference of each circle near the base is shown in table 1.

Circle Description No.
C Stone circle on Salapathala Maluwa. 22
D Circle on Welikonda. 27
E Circle on first Pesawa. 19
F Circle on second Pesawa. 20
G Circle on third Pesawa. 19
H Circle formed by plaster on the dome. 29

Table 1 Descriptions & number of Points of Circles at the Base of Stupa

The observation equation for the circle after linearizing using Taylor series and neglecting 2nd and higher orders is in the form of equation (3).













Due to the neglection of the second and higher orders of the Taylor series, results obtained by the above equations to be iterated until it reached to the specified tolerance levels.

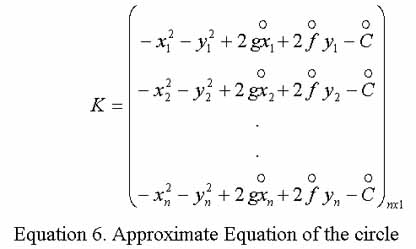
Computation
A computer programme was specially developed to solve the above equations due to the complex nature of the calculation and the iterative process. Hence a computer programme was developed to execute the above calculations using FORTRAN77 scientific programming language. All calculations were carried out in double precision mode (up to sixteen decimal places) to maintain required accuracy.

b>Results
Parameters of the best fitting circles after least squares adjustment are shown in table 2. Adopted ±1mm tolerance level was reached within three iterations. The parameters of the best fitting circles after least squares adjustment was given in table 2. Small variances of the results clearly indicate the high accuracy levels maintained in the field procedure. The mean of the centres of the six circles around the base was the best probable value of the centre of the stupa, which is having following co-ordinates.

North co-ordinate of the centre = 1538.7017±0.05
East co-ordinate of the centre = 8315.1568±0.05
The height to the top of the spire from the Salapathala Maluwa is 73 m.



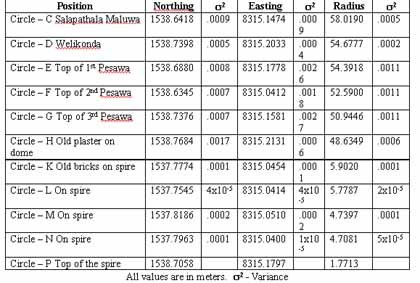
Table 2. Centre co-ordinates and the radius of each circle


Conclusion
The above results clearly show that the centre of the original dome was setout to an accuracy of ± 20 cm. These measurements are independent from the centre of the Koth Kerella. The centre of the Koth Kerella is approximately one meter south to the centre of the dome. Surprisingly the centre of the top of the ruined spire (Circle P) is within ±2cm to the computed coordinates of the centre. This procedure can be adopted to find out the original size of any other large monuments very accurately.

References
Dampegama, S.D.P.J., 1999. Interim Report of Abhayagiriya Stupa Survey Stage I

Smithers, J.G., Architectural Remains, Anuradhapura, Sri Lanka.

Urho A. Uotila , 1986. Notes On Adjustment Computations.