GISdevelopment.net ---> AARS ---> ACRS 2000 ---> GIS & Data Integration



A Surface Interpolation for Large-scale Representation of Terrain in An Urban Area

Yohko Shimura*, Shaobo Huang** and Ryosuke Shibasaki*
*Center for Spatial Information Science, University of Tokyo
**Center for Environmental Remote Sensing Center, Chiba University
4-6-1, Meguro-ku, Komaba, Tokyo 153-8505 Japan
Tel:+81-3-5452-6417 fax:+81-3-5452-6417
Email: yshimura@iis.u-tokyo.ac.jp


Key Words: urban space, triangulated irregular network (TIN), surface interpolation, three dimensional (3D) representation, boundary representation (BR) model.

Abstract:
Urban terrain surfaces have geometric characteristics such as discontinuities in terms of elevation and slope gradient. By introducing boundary representation ( BR )model to the terrain surface representation instead of conventional 2.5D type representation, such characteristics can be easily handled, though how to provide elevation data for the BR model efficiently is still an open question. With this background, this paper presents a surface interpolation method to represent terrain surface in urban space suitably. Through an example of the representation of terrain surface, it is demonstrated that the proposed surface interpolation method can be efficiently applied.

1.Introduction
Nowadays, the information society is growing dramatically. In a "flood of information", one of the key issues is how to organize data to extract useful information. By focusing the time and spatial position/extent that those data are referring to, we can analyze various types of data and information and uncover the hidden structure behind them. The movement that combines 3D CAD ( Computer Aided Design ) design data with survey data in GIS is becoming more active to improve efficiency in information distribution and sharing in urban planning, infrastructure construction and facility management.

It is very important to manage and utilize urban information in 3D GIS for urban disasters and urban designs, while we have kept road networks and buildings as 2D information. It is expected that 3D mapping technologies will be applied to many fields especially in car navigation system, urban planning, urban disaster.

Representation of terrain surface, especially large-scale detailed representation is a basis of urban 3D data because the height of buildings are determined against the terrain surface and the terrain surfaces play important roles in a number of simulations such as traffic simulation, flooding simulation etc.

Though urban terrain surface have geometric characters such as discontinuities in terms of elevation and slope gradient, terrain surface are conventionally interpolated based on an assumption that the surface is smoothly undulating. Many commercial GIS packages provide terrain surface interpolation methods as such. But if the terrain surface is interpolated based on such assumption, it is disable to represent urban space in 3D suitably.

On the other hand, calculating a large amount of coordinate data is necessary to represent 3D geographic objects and buildings in urban area. The surface in urban space has so complicated shapes that a large amount of elevation points are needed. With this reason, the method is necessity to interpolate the surface efficiently with both least and easily sampled points

This paper presents an improved interpolation method to represent terrain surface in an urban space in 3D, considering three basic requirements for 3D representation model of urban space as follows; (1) Ease of representation of a variety of geographic objects in urban space; (2) Efficiency in building and updating 3D special database; (3) Compatibility with existing map data and 3D presentation system

2. Existing interpolation methods
It needs much amount of points to represent urban spaces in 3D.But it's not easy to assign data to such amount of points respectively. Generally after sampling spatial data on the ground, unknown points about spatial characteristics are interpolated the value which is the most plausible between data points
  1. Thiessen polygons
    This method is based on the assumption that the best information is given by the nearest sampled point. This method is best for nominal data with a two dimensional array, but the level of accuracy on information in each polygon is not homogeneous because the size and shape of each polygon depends on sample layout.

  2. Trend surface analysis
    This method is to fit a surface (e.g. polynomial surface) by least squares through data points. This is the simplest method to describe long-large variations but the trend surface is very susceptible to outliers in the data.

  3. B-splines
    This method uses spline functions. They are piecewise functions fitted to small number of points exactly, while the same time ensuring that the joints between part of the curve and another are continuous.

  4. Method using moving average
    This method estimates values at un-sampled locations by the average of those of neighboring points. This method depends on the range of definition about ' around ' and the distribution of sampled points.
  5. Kriging
    This method is based on the assumption that statistical nature of variation can be expressed by the sum of three major components as follow; (1) a structural components (associated with a constant mean value or a constant trend) ; (2) a randam, spatially correlated component ; (3) a random noise. This method needs more computing time but usually yields quantitatively better results.

  6. Universal Kriging
    This method is an "improved" method to express local drifts based on Kriging as universal interpolation method. Universal Kriging enables to include the nature of ' drift ' in a structual component in Kriging.
However, these methods ( Method using moving average , Kriging, Universal Kriging) represent terrain surface smoothly. Therefore, these can't represent geometrical discontinuous such as break lines and step lines suitably.

3. The outline of surface interpolation methods
Existing surface interpolation methods usually assume that terrain surfaces are smooth. But the discontinuities of slopes and elevations are often the case in urban areas. The examples of discontinuities are shown in figure3-1

Figure3-1 the example of discontinuities

In the large-scale representation of urban terrain surfaces, such discontinuity have to be represented faithfully, while smooth surface representation may cause no serious problems in small scale representation of urban areas. The conventional surface interpolation methods can be used for the smallest scale representation of rural terrain area, though they cannot be directly applied into large scale representation to urban terrain surfaces.

This paper presents an improved interpolation method for large scale urban terrain surface representation to avoid such artifacts using road surface elevation data and boundary data which can be easily acquired both with air-based and ground-based surveying methods.The method allows us to take into account geometric characteristics or constraints such as discontinuity of elevation and slope gradients, smooth changes of road surface elevation. Interpolated surfaces are represented by triangular plane patches (TIN representation).

The smoother terrain surfaces are, the larger the sum of the square of inner-products of unit normal vectors of neighbouring triangular planes is. The surfaces are interpolated so as to maximize the sum of the square of inner-products of unit normal vectors of neighbouring triangular planes in urban space under such constraint conditions as keeping discontinuity of elevation and slope gradients at specified locations.

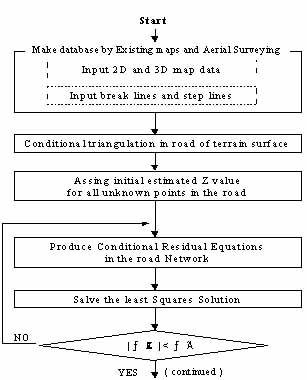
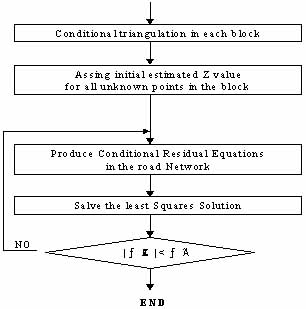
The basic process of the surface interpolation is shown in figure3-2. The surface interpolation process consists of five parts as follow.
  1. 3D coordinates (x, y, z) of selected elevation points (known points) and 2D coordinates (x, y,) of the rest (unknown points) are given.
  2. The geometric constraint conditions or structural features such as break lines and step lines are given. Additional constraint conditions can be added such that ground floor of buildings is flat (all points constituting the boundary should have identical elevation values).
  3. TIN network is generated based on Delaunay triangulation so as to include break lines and step lines as edges in the TIN network.
  4. Estimate of a road network are estimated through the "smooth" surface interpolation.
  5. Elevations of terrain surfaces are estimated in each block respectively taking the geometric constraints conditions into account.

Figure3-2 the basis process of surface interpolation

4. The case study in ROPPONGI area and its conclusion
A example of the surface interpolation has been made in ROPPONGI area around ROPPONGI and NOGIZAKA station in Tokyo, Japan. The range of study area in about 300m by 700m.There are about fifty blocks in the area. And more than 500buildings and other man-made objects are located in its terrain surface. In its 2D mapping data, more than twenty thousands points and edges are existing..

Figure 4-1 the air-bone picture in ROPPOMGI

This area has much geographical characters such as surfaces cutting into the ground, residential area which have many break lines, avenues which are smoothly undulating. The detailed results of the case study will be presented at the conference.

5. Conclusion
The terrain surface in urban areas have geographic characters such as discontinuities in terms of elevation and steepness of slopes. Under these geometric conditions, the proposed surface interpolation enables us to estimate Z values of spatial objects from some observed elevation data and save much time and labor in modeling 3D spatial objects in an urban space.

Comparing between the surface conditions of urban area by air-born sueveying and the representation of urban area by both this improved and conventional method, this example suggests that this proposed surface interpolation method represents urban space in 3D more suitably than conventional one.

References:
  1. P.A.Burrough, Principle of Geographical Information System for Land Resources Assessment, Clarenden Press, Oxford, 1986
  2. J.Raper, Three Dimensional Applications in Geographic Information, 1989, Dept. of Geography, Taylor and Francis Ltd. 1989
  3. R.Shibasaki and Huang Shaobo, The Representation of Terrain Surface and Its Interpolation Method for large Scale Digital Maps in An Urban Area, symposium of japan Society of Photogrametric and Remote Sensing, tokyo, May. 1992