| GISdevelopment.net ---> AARS ---> ACRS 2000 ---> Agriculture |
Multispectral Image
Compression using FCM-Based Vector Quantization
Supoj MONGKOLWORAPHOL, Yuttapong RANGSANSERI and Punya THITIMAJSHIMA
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand
Tel: (66-2) 326-9967, Fax: (66-2) 326-9086
E-mail: Supoj.mongkolworaphol@compaq.com mr_uthai@hotmail.com, kryuttha@kmitl.ac.th
Supoj MONGKOLWORAPHOL, Yuttapong RANGSANSERI and Punya THITIMAJSHIMA
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand
Tel: (66-2) 326-9967, Fax: (66-2) 326-9086
E-mail: Supoj.mongkolworaphol@compaq.com mr_uthai@hotmail.com, kryuttha@kmitl.ac.th
Keywords: Image Compression, Vector
Quantization, FCM
Abstract:
Image compression is the process of reducing the number of bits required to represent an image. Vector Quantization method (VQ) is a method to deal with this operation. With this method a set of data points is encoded by a reduced set of reference vectors (the codebook). VQ is useful in compressing data that arises in wide range applications and it can achieve better compression performance than any conventional coding techniques which based on the encoding of scalar quantities. This paper presents a multispectral image compression method using Vector Quantization technique based on Fuzzy c-Means (FCM). In this method we first use FCM algorithm to generate a good initial codebook. A modified version of FCM is used to reduce the computational time. Experimental results are shown to illustrate the performance of the proposed method.
1. Introduction
Image Compression is a process of reducing the number of bits required to represent an image. There are several methods to compress an image data. One popular method is Vector Quantization (VQ). VQ was used for compressing data in wide range applications, including image processing (Gray, 1984), (Nasrabadi, 1988), speech processing (Makhoul, 1985), facsimile transmission (Netravali, 1980) and weather satellites (Elachi, 1987). In this method the training vectors in the image are encoded by a reduced set of reference vectors (the codebook). From rate distortion theory, it can be shown that VQ can achieve better compression performance than any conventional coding technique which based on the encoding of scalar quantities (Gray, 1984). The objective of VQ is to design the codebook. An optimum VQ system is that one uses a codebook that yields the least average distortion of the reconstructed image. Other methods for designing codebooks have been proposed in (Linde, 1980), (Hsieh, 1992), (Hsieh, 1991), (Wu, 1994). The most popular one is the LBG algorithm (Linde, 1980). In this paper we use FCM to design the codebook in Vector Quantization process. The major problem of this method is the huge execution time in the FCM process. So, this paper will also present the modification on the FCM algorithm that can reduce the execution time in each iteration.
2. Fuzzy C-Means Clustering Technique
The fuzzy c-means (FCM) algorithm (Bezdek, 1984) is an iterative clustering method that used to partition a data set. The objective of FCM segmentation is to compute the cluster centers and generate the class membership matrix (Zadeh, 1965). This class membership matrix is a cxN matrix, where c is the number of groups and N is the number of samples of image in n-space. Each column of the class membership matrix is the distribution of the class attribute of its corresponding sample. Each row of the class membership matrix is the membership value of each sample to be a member of that particular cluster.
An optimal fuzzy c-partition is one that minimizes the generalized least-squared errors function. We can explain the fuzzy clustering by the following equation.
Minimize: Jm (U,v) = 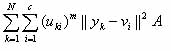
Where : Y = {y1, y2, y3, …, yN} Ì R n is the data set,
c is the number of clusters in Y: 2 £ c < n,
m is a weighting exponent: 1 £ m < ¥,
U = {uki} is the fuzzy c-partition of Y,
||y k-vi||A is an induced a-norm on Rn, and,
A is a positive-definite (nxn) weight matrix.
The weighting exponent m has the effect of reducing the squared distance error by an amount that depends on the observation's membership in the cluster. As m ® 1 , the partitions that minimize Jm become increasingly hard. Conversely, higher values of m tend to soften a samples cluster membership, and the partition becomes increasingly blurred. Generally m must be selected by experimental means.
The first step of FCM algorithm is generate an initial random membership matrix and use this random membership matrix as weight of each samples to belong to each cluster. Then computes the centroid of each cluster. The new cluster centers are used to update the membership matrix. The updated membership matrix is compared with the previous ones. If the difference is greater than some threshold, then another iteration is computed, otherwise the algorithm is stopped. The algorithm is shown below. The notation x (t) signifies the value of variable x at iteration t.
The FCM Algorithm
1. set value for c, A, m, e, and the loop counter t = 1
2. create a random Nxc membership matrix U
3. compute each cluster centroid by equation
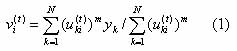
4. update the membership matrix by equation
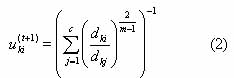
where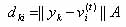
5. If max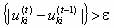 increment t and go to step 3.
increment t and go to step 3.
3. The Modified Fuzzy C-Means Algorithm
From equation (1) we can find that each cluster center vi is computed as the weighted average of samples in the data set Y. The weight used for each sample is that sample's membership in the ith cluster. In the original algorithm this is computed by performing a pass over the entire data set and membership matrix.
The following describes an improvement to the algorithm whereby the computation of cluster centers is performed in sequence with the membership matrix updating. This effectively eliminates an entire pass of the data set. The outcome is not a decrease in the number of iterations required for convergence, but decrease in the time of each iteration.
We maintain two extra data structures, a cxn matrix, P = {pi}, and a vector q of length c. We can obtain these two matrix from the first iteration when the random membership matrix is created. If we represent the numerator and denominator of equation (1) by P and q, respectively, then keep them as initial values. So now the equation (1) is replaced by equation (3)
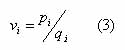
where pi is a vector of length n, and q.i is a scalar. The dot-i subscript is used to avoid confusion between vectors and scalars.
Each time an element uki of the membership matrix is computed there is an increment in the numerator of equation (1), that is an increase in pi of
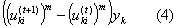
And an increment in the denominator of equation (1), that is, an increase in q.i of
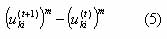
These increments are accumulated into P and q respectively as the membership matrix is updated. At the beginning of the next iteration the new cluster centers are again computed by equation (3).
The Modified FCM algorithm
1. set values for c, A, m, e, and loop counter t=1
2. create a random Nxc membership matrix U(t)
3. initialize data structures P and q using equation (1)
4. compute c cluster centers using equation (3)
5. update the membership matrix using equation (2) as each membership is computed, increment the corresponding element of P and q using equation (4) and equation (5)
6. if max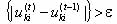 increment t and
go to step 4.
increment t and
go to step 4.
4. FCM-Based Vector Quantization
In this paper, FCM process is used to calculate the reference vector or average vector from each cluster. The output of this process is a membership matrix and a set of reference vectors that used to design the vector quantization codebook. The training vector will be encoded with this codebook. The algorithm of this compression method is shown in Figure 1.
Figure 1:
Figure 1: Block diagram of the proposed method.
The evaluation was performed by using the following measures:
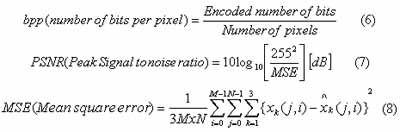
5. Experimental Results
The proposed image compression algorithm was implemented using Matlab. Several multispectral images were used in experimental. Table 1 shows the experimental results when applied to a three-band (24 bits) image, size of 256x256 pixels. The input image size is 196 Kbyte. The experiments were carried out with the number of clusters of 4, 16 and 64.
Table 1: Experimental
results.
6. Conclusion
The experimental result shown that the proposed method can compress the multispectral image data. The compressibility of this method and the image distortion from quantizing process depends on the number of clusters used in FCM process. The major problem of this method is the execution time spent in clustering process caused by the computation complexity of FCM algorithm even we use the modified version of FCM.
References
Abstract:
Image compression is the process of reducing the number of bits required to represent an image. Vector Quantization method (VQ) is a method to deal with this operation. With this method a set of data points is encoded by a reduced set of reference vectors (the codebook). VQ is useful in compressing data that arises in wide range applications and it can achieve better compression performance than any conventional coding techniques which based on the encoding of scalar quantities. This paper presents a multispectral image compression method using Vector Quantization technique based on Fuzzy c-Means (FCM). In this method we first use FCM algorithm to generate a good initial codebook. A modified version of FCM is used to reduce the computational time. Experimental results are shown to illustrate the performance of the proposed method.
1. Introduction
Image Compression is a process of reducing the number of bits required to represent an image. There are several methods to compress an image data. One popular method is Vector Quantization (VQ). VQ was used for compressing data in wide range applications, including image processing (Gray, 1984), (Nasrabadi, 1988), speech processing (Makhoul, 1985), facsimile transmission (Netravali, 1980) and weather satellites (Elachi, 1987). In this method the training vectors in the image are encoded by a reduced set of reference vectors (the codebook). From rate distortion theory, it can be shown that VQ can achieve better compression performance than any conventional coding technique which based on the encoding of scalar quantities (Gray, 1984). The objective of VQ is to design the codebook. An optimum VQ system is that one uses a codebook that yields the least average distortion of the reconstructed image. Other methods for designing codebooks have been proposed in (Linde, 1980), (Hsieh, 1992), (Hsieh, 1991), (Wu, 1994). The most popular one is the LBG algorithm (Linde, 1980). In this paper we use FCM to design the codebook in Vector Quantization process. The major problem of this method is the huge execution time in the FCM process. So, this paper will also present the modification on the FCM algorithm that can reduce the execution time in each iteration.
2. Fuzzy C-Means Clustering Technique
The fuzzy c-means (FCM) algorithm (Bezdek, 1984) is an iterative clustering method that used to partition a data set. The objective of FCM segmentation is to compute the cluster centers and generate the class membership matrix (Zadeh, 1965). This class membership matrix is a cxN matrix, where c is the number of groups and N is the number of samples of image in n-space. Each column of the class membership matrix is the distribution of the class attribute of its corresponding sample. Each row of the class membership matrix is the membership value of each sample to be a member of that particular cluster.
An optimal fuzzy c-partition is one that minimizes the generalized least-squared errors function. We can explain the fuzzy clustering by the following equation.
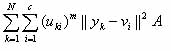
Where : Y = {y1, y2, y3, …, yN} Ì R n is the data set,
c is the number of clusters in Y: 2 £ c < n,
m is a weighting exponent: 1 £ m < ¥,
U = {uki} is the fuzzy c-partition of Y,
||y k-vi||A is an induced a-norm on Rn, and,
A is a positive-definite (nxn) weight matrix.
The weighting exponent m has the effect of reducing the squared distance error by an amount that depends on the observation's membership in the cluster. As m ® 1 , the partitions that minimize Jm become increasingly hard. Conversely, higher values of m tend to soften a samples cluster membership, and the partition becomes increasingly blurred. Generally m must be selected by experimental means.
The first step of FCM algorithm is generate an initial random membership matrix and use this random membership matrix as weight of each samples to belong to each cluster. Then computes the centroid of each cluster. The new cluster centers are used to update the membership matrix. The updated membership matrix is compared with the previous ones. If the difference is greater than some threshold, then another iteration is computed, otherwise the algorithm is stopped. The algorithm is shown below. The notation x (t) signifies the value of variable x at iteration t.
The FCM Algorithm
1. set value for c, A, m, e, and the loop counter t = 1
2. create a random Nxc membership matrix U
3. compute each cluster centroid by equation
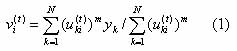
4. update the membership matrix by equation
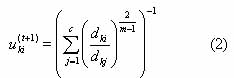
where
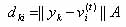
5. If max
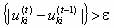 increment t and go to step 3.
increment t and go to step 3.
3. The Modified Fuzzy C-Means Algorithm
From equation (1) we can find that each cluster center vi is computed as the weighted average of samples in the data set Y. The weight used for each sample is that sample's membership in the ith cluster. In the original algorithm this is computed by performing a pass over the entire data set and membership matrix.
The following describes an improvement to the algorithm whereby the computation of cluster centers is performed in sequence with the membership matrix updating. This effectively eliminates an entire pass of the data set. The outcome is not a decrease in the number of iterations required for convergence, but decrease in the time of each iteration.
We maintain two extra data structures, a cxn matrix, P = {pi}, and a vector q of length c. We can obtain these two matrix from the first iteration when the random membership matrix is created. If we represent the numerator and denominator of equation (1) by P and q, respectively, then keep them as initial values. So now the equation (1) is replaced by equation (3)
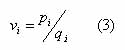
where pi is a vector of length n, and q.i is a scalar. The dot-i subscript is used to avoid confusion between vectors and scalars.
Each time an element uki of the membership matrix is computed there is an increment in the numerator of equation (1), that is an increase in pi of
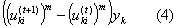
And an increment in the denominator of equation (1), that is, an increase in q.i of
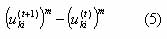
These increments are accumulated into P and q respectively as the membership matrix is updated. At the beginning of the next iteration the new cluster centers are again computed by equation (3).
The Modified FCM algorithm
1. set values for c, A, m, e, and loop counter t=1
2. create a random Nxc membership matrix U(t)
3. initialize data structures P and q using equation (1)
4. compute c cluster centers using equation (3)
5. update the membership matrix using equation (2) as each membership is computed, increment the corresponding element of P and q using equation (4) and equation (5)
6. if max
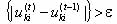 increment t and
go to step 4.
increment t and
go to step 4. 4. FCM-Based Vector Quantization
In this paper, FCM process is used to calculate the reference vector or average vector from each cluster. The output of this process is a membership matrix and a set of reference vectors that used to design the vector quantization codebook. The training vector will be encoded with this codebook. The algorithm of this compression method is shown in Figure 1.
Figure 1: Block diagram of the proposed method.
The evaluation was performed by using the following measures:
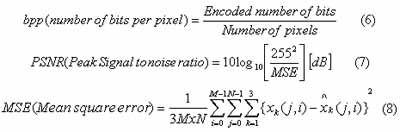
5. Experimental Results
The proposed image compression algorithm was implemented using Matlab. Several multispectral images were used in experimental. Table 1 shows the experimental results when applied to a three-band (24 bits) image, size of 256x256 pixels. The input image size is 196 Kbyte. The experiments were carried out with the number of clusters of 4, 16 and 64.
| Number of clusters | bpp | PSNR (dB) | MSE |
| 4 | 2.0016 | 22.0651 | 404.1790 |
| 16 | 4.068 | 27.4127 | 117.9196 |
| 64 | 6.0293 | 31.2498 | 48.7638 |
The experimental result shown that the proposed method can compress the multispectral image data. The compressibility of this method and the image distortion from quantizing process depends on the number of clusters used in FCM process. The major problem of this method is the execution time spent in clustering process caused by the computation complexity of FCM algorithm even we use the modified version of FCM.
References
- Bezdek, J.C., Ehrlich, R., and Full, W., 1984. FCM : The fuzzy c-means clustering algorithm. Computers and Geosciences, 10, pp. 191-203.
- Elachi, C., 1987. Introduction to The Physics of Remote Sensing. Intersciences, New York.
- Gray, R.M., 1984. Vector quantization. IEEE ASSP Magazine, 1(2), pp. 4-29.
- Hsieh, C.H., 1992. DCT based codebook design for vector quantization of images. IEEE Trans. Circuits and Systems, 2, pp. 40-1-409.
- Hsieh, C.H., Lu. P.C. and Chung. J.C., 1991. Fast codebook generation algorithm for vector quantization of images. Pattern Recogn. Lett., 12, pp. 605-609.
- Linde, Y., Buzo, A. and Gray, R.M., 1980. An algorithm for vector quantization design. IEEE Trans. Commun., 28, pp. 84-95.
- Makhoul, J., Roucos, S. and Gish, H., 1985. Vector quantization in speech coding, Proc. IEEE, 73(11), pp. 1551-1588.
- Nasrabadi, N. and King, R.A., 1988. Image coding using vector quantization: A review. IEEE Trans. Commun., 36(8), pp. 957-971.
- Netravali, A.N. and Mounts F.W., 1980. Ordering techniques for facsimile coding: A review. Proc. IEEE, 68, pp. 796-807.
- Wu, X. and Guan, L., 1994. Acceleration of the LBG algorithm. IEEE Trans. Commun., 42, pp. 1518-1523.
- Zadeh, L.A, 1965. Fuzzy sets. Information and Control, 8, pp. 338-353.