| GISdevelopment.net ---> AARS ---> ACRS 2000 ---> Image Processing |
Urban Image Analusys Using
Adaptive Resonance Theory
Supoj MONGKOLWORAPHOL, Yuttapong RANGSANSERI and Punya THITIMAJSHIMA
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand
Tel: (66-2) 326-9967, Fax: (66-2) 326-9086
E-mail: Supoj.mongkolworaphol@compaq.com ,ktpunya@kmitl.ac.th, kryuttha@kmitl.ac.th
Supoj MONGKOLWORAPHOL, Yuttapong RANGSANSERI and Punya THITIMAJSHIMA
Department of Telecommunications Engineering, Faculty of Engineering
King Mongkut's Institute of Technology Ladkrabang, Bangkok 10520, Thailand
Tel: (66-2) 326-9967, Fax: (66-2) 326-9086
E-mail: Supoj.mongkolworaphol@compaq.com ,ktpunya@kmitl.ac.th, kryuttha@kmitl.ac.th
Keyword: Urban Image Analysis, Adaptive
Resonance Theory, Neural Network
Abstract
In this paper multispectral images of an urban environment are analyzed and interpreted by means of a neural network approach. In particular, the advantages found by using Adaptive Resonance Theory network of the data are shown and commented. We used the ART2 structure accepts floating-point data, so that each input can be for each pixel directly the vector of the gray level values at each band. This choice is due to the attempt to simplify algorithm as much as possible. Experiments carried out with JERS-1 images will be given.
1. Introduction
The analysis of urban structure is gaining more and more interest, due to the fact that this kind of study may be useful for a number of applications, e.g. settlement detection, population estimation, mapping of land use and changes, assessment of urban activities on the landscape. In particular, remote sensing has a growing importance in this field; indeed, it gives the possibility to observe at difference scales and without interference the urban environment at rates that are clearly impossible for a study on the ground. Computer-aided classification of earth terrain based on the segmentation of remotely sensed image, e.g., Landsat, JERS-1, ADEOS, and SPOT, has provided an alternate, effective method for the above mapping purpose. Adaptive Resonance Theory (ART) architecture is neural networks that carry out stable self-organization of recognition codes for arbitrary sequence of input pattern. Adaptive Resonance Theory first emerged from an analysis of the instabilities inherent in feed forward adaptive coding structure (Grossberg, 1976a, 1976b). More recent work has led to the development of three classes of ART neural network architecture, specified as system differential equations: ART1 and ART2 (Carpenter, 1991). By especially ART2 self-organizes recognition categories for arbitrary sequences of either binary or analog inputs. ART2 is designed to perform for continuous-valued input vectors the same type of tasks as ART1 does for binary input vectors. The differences between ART2 and ART1 reflect the modifications need to accommodate patterns with continuous-valued components. The more complex F1 field of ART2 is necessary because continuous-valued input vector may be arbitrarily close together. The F1 field in ART2 includes a combination of normalization and noise suppression, in addition to the comparison of the bottom-up and top-down signals needed for the reset mechanism.

Figure 1: ADEOS image of. Bangkok area.
![]()
Figure 2: Typical ART2 architecture.
The ART2 architecture (Carpenter, 1991), (Fausett, 1994), which consists of two main modules: the attentional and the orienting modules. The attentional module is further divided into two fields: an input representation field F1 and a category representation field F2. F1 consist of (w, x, v, u, p, and q), each having n neural. The F2 field contains only one layer, which is denote by Y and serves as a competitive layer. There are top-down and bottom-up full connections between F1 and F2. Pattern prototypes are to be preserved on these connections. The input signal is S = (S1,…,Si,…,Sn) continues to be sent while all of the sections to be described are performed. At the beginning of a learning trail, all activation is set to zero. The computation within the F1 layer can be thought of as originating with the computation of the activation of unit Ui (the activation of unit Vi normalized to approximately unit length). Next, a signal is sent from each unit Ui to its associated units Wi and Pi. The activation of units Wi and Pi are then computed. Unit Wi sum the signal it received from Ui and the input signal Si. Pi sum the signal it receives from Ui and the top-down signal it receives if there is an active F2 unit. The activation of Xi and Qi are normalized version of the signal at Wi and Pi. An activation function is applied at each of units before the signal is sent to Vi. Vi then sums the signals if receives concurrently from Xi and Qi; this completes one cycle of updating the F1 layer.
The activates of the F1 layer are formulated, respectively, as
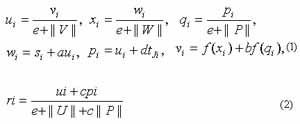
After the activation of the F1 units have reached equilibrium, the Pi units sent their signals to the F2 layer, where the winner-take-all competition chooses the candidate cluster unit to learn the input pattern. The units Ui and Pi in the F1 layer also send signal to the corresponding reset unit Ri. The reset mechanism can check for a reset each time it receives signal from Pi and Ui, which aggregates the activities of Pi and Ui and transmits the result to the vigilance parameter. Vigilance parameter then decides whether or not a reset signal is emitted to the layer Y in field F2. There are also gain control units in the network. They normalize activity patterns over layers. (Fausett , 1994)
We propose an unsupervised approach to the neural classification of the source images. This choice is due to the attempt to simplify as mush as possible the detection of the urban features by the automatic analysis of the data. Therefore, we look for competitive algorithms suitable for the task. We need neural networks able to aggregate data in consistent clusters. The ART2 neural algorithm respectively, as
Step0. Initial parameter
Step1. Perform the specified number of training
Step2. For each input vector update F1unit
Step3. Update F1 unit activation again
Step4. Compute signals to F2 units
Step5. Check for reset
Step6. Perform the specified of learning iterations
Step7. Update weights for wining unit
Step8. Update F1 unit again
Step9. Test stopping condition for weight update
Step10. Test stopping condition for number of training
3. Experimental Resaults

Figure 3: Classification result of the area in Fig 1.
The classification was applied to a three-band image of Bangkok (Fig. 1). The image was recorded by the ADEOS satellite. We applied the previously presented neural classification algorithm to this data set by OPS image the result are completely satisfying. The neural classification starts by applying an ART network looking for spectral aggregation of the pixel. The three-band data are aggregate an input vector in order to match the ability of ART networks to discriminated against different pattern. Fig. 3 presents spectral classification result obtained by the ART2 algorithm and we found very difficult to tune the network parameters to obtain satisfying result.
4. Conclusion
This work simplifies and completes the ART approach to remote sensing data analysis introduced in (Silva, 1997). We apply the methodology to urban environments and multiband data introduce a clustering step to solve class redundancy and high lightening the advantages and disadvantages of data analysis. The results presented, corresponding to a part of data, are satisfying, and it can be using to analysis another image for classification by computer-aided.
5. Acknowledgement
The authors wish to thank the National Research Council of Thailand (NRCT) for providing the satellite image data
References
Abstract
In this paper multispectral images of an urban environment are analyzed and interpreted by means of a neural network approach. In particular, the advantages found by using Adaptive Resonance Theory network of the data are shown and commented. We used the ART2 structure accepts floating-point data, so that each input can be for each pixel directly the vector of the gray level values at each band. This choice is due to the attempt to simplify algorithm as much as possible. Experiments carried out with JERS-1 images will be given.
1. Introduction
The analysis of urban structure is gaining more and more interest, due to the fact that this kind of study may be useful for a number of applications, e.g. settlement detection, population estimation, mapping of land use and changes, assessment of urban activities on the landscape. In particular, remote sensing has a growing importance in this field; indeed, it gives the possibility to observe at difference scales and without interference the urban environment at rates that are clearly impossible for a study on the ground. Computer-aided classification of earth terrain based on the segmentation of remotely sensed image, e.g., Landsat, JERS-1, ADEOS, and SPOT, has provided an alternate, effective method for the above mapping purpose. Adaptive Resonance Theory (ART) architecture is neural networks that carry out stable self-organization of recognition codes for arbitrary sequence of input pattern. Adaptive Resonance Theory first emerged from an analysis of the instabilities inherent in feed forward adaptive coding structure (Grossberg, 1976a, 1976b). More recent work has led to the development of three classes of ART neural network architecture, specified as system differential equations: ART1 and ART2 (Carpenter, 1991). By especially ART2 self-organizes recognition categories for arbitrary sequences of either binary or analog inputs. ART2 is designed to perform for continuous-valued input vectors the same type of tasks as ART1 does for binary input vectors. The differences between ART2 and ART1 reflect the modifications need to accommodate patterns with continuous-valued components. The more complex F1 field of ART2 is necessary because continuous-valued input vector may be arbitrarily close together. The F1 field in ART2 includes a combination of normalization and noise suppression, in addition to the comparison of the bottom-up and top-down signals needed for the reset mechanism.

Figure 1: ADEOS image of. Bangkok area.
Figure 2: Typical ART2 architecture.
The ART2 architecture (Carpenter, 1991), (Fausett, 1994), which consists of two main modules: the attentional and the orienting modules. The attentional module is further divided into two fields: an input representation field F1 and a category representation field F2. F1 consist of (w, x, v, u, p, and q), each having n neural. The F2 field contains only one layer, which is denote by Y and serves as a competitive layer. There are top-down and bottom-up full connections between F1 and F2. Pattern prototypes are to be preserved on these connections. The input signal is S = (S1,…,Si,…,Sn) continues to be sent while all of the sections to be described are performed. At the beginning of a learning trail, all activation is set to zero. The computation within the F1 layer can be thought of as originating with the computation of the activation of unit Ui (the activation of unit Vi normalized to approximately unit length). Next, a signal is sent from each unit Ui to its associated units Wi and Pi. The activation of units Wi and Pi are then computed. Unit Wi sum the signal it received from Ui and the input signal Si. Pi sum the signal it receives from Ui and the top-down signal it receives if there is an active F2 unit. The activation of Xi and Qi are normalized version of the signal at Wi and Pi. An activation function is applied at each of units before the signal is sent to Vi. Vi then sums the signals if receives concurrently from Xi and Qi; this completes one cycle of updating the F1 layer.
The activates of the F1 layer are formulated, respectively, as
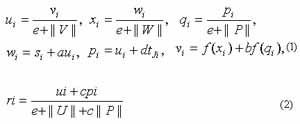
After the activation of the F1 units have reached equilibrium, the Pi units sent their signals to the F2 layer, where the winner-take-all competition chooses the candidate cluster unit to learn the input pattern. The units Ui and Pi in the F1 layer also send signal to the corresponding reset unit Ri. The reset mechanism can check for a reset each time it receives signal from Pi and Ui, which aggregates the activities of Pi and Ui and transmits the result to the vigilance parameter. Vigilance parameter then decides whether or not a reset signal is emitted to the layer Y in field F2. There are also gain control units in the network. They normalize activity patterns over layers. (Fausett , 1994)
We propose an unsupervised approach to the neural classification of the source images. This choice is due to the attempt to simplify as mush as possible the detection of the urban features by the automatic analysis of the data. Therefore, we look for competitive algorithms suitable for the task. We need neural networks able to aggregate data in consistent clusters. The ART2 neural algorithm respectively, as
Step0. Initial parameter
Step1. Perform the specified number of training
Step2. For each input vector update F1unit
Step3. Update F1 unit activation again
Step4. Compute signals to F2 units
Step5. Check for reset
Step6. Perform the specified of learning iterations
Step7. Update weights for wining unit
Step8. Update F1 unit again
Step9. Test stopping condition for weight update
Step10. Test stopping condition for number of training
3. Experimental Resaults

Figure 3: Classification result of the area in Fig 1.
The classification was applied to a three-band image of Bangkok (Fig. 1). The image was recorded by the ADEOS satellite. We applied the previously presented neural classification algorithm to this data set by OPS image the result are completely satisfying. The neural classification starts by applying an ART network looking for spectral aggregation of the pixel. The three-band data are aggregate an input vector in order to match the ability of ART networks to discriminated against different pattern. Fig. 3 presents spectral classification result obtained by the ART2 algorithm and we found very difficult to tune the network parameters to obtain satisfying result.
4. Conclusion
This work simplifies and completes the ART approach to remote sensing data analysis introduced in (Silva, 1997). We apply the methodology to urban environments and multiband data introduce a clustering step to solve class redundancy and high lightening the advantages and disadvantages of data analysis. The results presented, corresponding to a part of data, are satisfying, and it can be using to analysis another image for classification by computer-aided.
5. Acknowledgement
The authors wish to thank the National Research Council of Thailand (NRCT) for providing the satellite image data
References
- Carpenter A. G., Grossberg S. and Rosen. B. D., 1991. ART 2-A:, an
adaptive resonance algorithm for rapid category learning and
recognition. neural network, (4), pp. 493-504.
- Fausett L., 1994. Fundamentals of Neural Network Architecture
Algorithm and Application. Prentice-Hall.
- Silva S. and Caetano M., 1997. Using Artificial Recurrent Neural
Nets to Identify Spectral and Spatial Pattern for Satellite Imagery
Classification of Urban Area. In: Neurocomputation in Remote Sensing
Data Analysis, I. Kanellopoulos et al. (eds.), Springer: Berlin, pp.
151-159.