The polynomial least squares operation (PoLeS): A method for reducing noise in NDVI time series data

The polynomial least squares operation (PoLeS): A method for reducing noise in NDVI time series data

Jose Edgardo L. Aban
Center for Environmental Remote Sensing (CEReS)
Chiba University
1-33 Yayoi, Inage, Chiba-ken, Japan
Tel: +81-43-290-3965
Fax: +81-43-290-3857
E-mail: aban@ceres.cr.chiba-u.ac.jp
Japan

Ryutaro Tateishi
Center for Environmental Remote Sensing (CEReS)
Chiba University
1-33 Yayoi, Inage, Chiba-ken, Japan
Tel: +81-43-290-3965
Fax: +81-43-290-3857
E-mail: aban@ceres.cr.chiba-u.ac.jp
Japan

Renchin Tsolmon
Center for Environmental Remote Sensing (CEReS)
Chiba University
1-33 Yayoi, Inage, Chiba-ken, Japan
Tel: +81-43-290-3965
Fax: +81-43-290-3857
E-mail: mailto:aban@ceres.cr.chiba-u.ac.jp"
Japan

Abstract
The Polynomial Least Squares Operation (PoLeS) is proposed as an alternative novel technique used to reduce noise in the Normalized Difference Vegetation Index (NDVI) time-series from the Advanced Very High Resolution Radiometer (AVHRR) data. The PoLeS method preserves more valuable elements of the NDVI profile and considers both cloud contamination that depress the NDVI profile, and anistropic sources of high value noise which tend to have the opposite effect. Previous profile extraction algorithms only tend to discard low frequency NDVI values. Whereas, other previous algorithms introduce a bias due to the assumption that a lower values of NDVI are considered only as noise while retaining higher values, the PoLeS does not suffer from such a bias. Furthermore, the PoLeS preserves the inherent variability in the NDVI data.

Introduction
The Normalize Difference Vegetation Index (NDVI) remains to be the most common measure of physiological and biochemical plant processes. The spectral response of vegetation as measured by the NDVI can be defined as the difference between near infrared and the red reflectance divided by the sum of the two. NDVI values are closely linked to plant cover under many conditions. A generalized NDVI profile for vegetation cover is characterized by an increasing trend (rising) as plant cover increases (growth) reaches a peak, or a plateau and falls off as the plant undergoes change in leaf coloration and senescence, and eventually towards death. In areas where the vegetation canopy changes very little with time, e.g., deserts and tropical rainforests, the NDVI profiles usually do not show marked increases or decreases in value. Thus the NDVI can provide a means for describing the vegetation phenology. Furthermore, the relationship on NDVI on cover, and thus the profile, may be affected if the vegetation is stressed in a way which affects the canopy. Also, the relationship between NDVI and plant cover is known to vary between vegetation types and so different biomes can have different NDVI profiles. Also, the NDVI profiles for a given vegetation type can vary from area to area and year to year depending on the existing weather.

Since 1982, the National Oceanic and Atmospheric Administration’s (NOAA) Advanced Very High Resolution Radiometers (AVHRR) provide daily Earth observations. From these data, NDVI profiles have been built and complied through the years. Such multi-annual profiles data have been used to monitor primary production (Prince and Tucker 1986), to study the dynamics of major biomes (Malingreau,1986), for land cover classification (Townsend et al. 1991), and for estimation of crop yield (Bartholome’, 1991).

Changes in the NDVI derived from AVHRR data are usually indicative if changes in the surface conditions, most predominantly changes in vegetation. However, there are other extrinsic factors that cause changes in the overall NDVI profile, among which are cloud contamination, atmospheric variability and bi-directional effects (Gutman 1991); these changes are usually considered as undesirable noise in vegetation studies. A widely used method to reduce this noise is the Maximum Value Composite (MVC) technique proposed by Holben (1986) and those of Prince and Justice (1991). The MVC retains the highest NDVI value for a given location over a pre-defined compositing period, the assumption being that all contamination depress NDVI values. The technique works best with a long compositing period, around 2 to 4 weeks. But too long a period will distort the profile and may completely mask short term changes in vegetation condition. Short compositing periods are more generally used for example, the standard NOAA Product, the Global Vegetation Index (GVI), is created on a weekly basis (NOAA, 1990) though this still retains a lot of noise.

A widely used technique is that of the Best Index Slope Extraction or the BISE (Viovy et al, 1992). From the first date of the time series, the BISE algorithm searches forward and considers the succeeding point if it is of higher value than the preceding point. Where the NDVI value from one day to the next decreases, this decrease is only accepted if there is no point in a pre-defined period of time (called a sliding period) with a value greater than 20 percent of the difference between the first low value and the previous high value. If such a high value is encountered it is selected and the low point is ignored.

A similar technique called the Temporal Window Operation (TWO) was developed by Park et al (1998). The TWO proceeds by looking at the trajectory of each pixel and finding the low NDVI value and replacing this by a linearly interpolated value. The algorithm starts at the beginning of the NDVI curve (start point) and checks whether the NDVI for the current period is equal to or greater than the previous NDVI value within the window. If it is higher, current value is assigned as the start point of next window. If there is no higher value within the window, the next biggest value is chosen as the next start point, with the lower values being replaced by linearly interpolated values from the current start point to the next.

The Maximum Value Interpolated (MVI) is an enhancement of the MVC (Taddei, 1997). The MVI method consists of recording not only the NDVI maximum value within a period (e.g., a month) , but also the day when the value was recorded. Through simple linear interpolation between these points it is possible to detect, fo r each time period, a representative NDVI value.

Here we present another method for extracting NDVI profiles from ten-day composite data, called the Polynomial Least Squares Operation (PoLeS). The seasonal characteristics of vegetation are generally predictable , depending on ecoclimatic zonation (Prentice, 1990). The PoLeS method accounts for the phenomenon that plant growth and development is often asymmetric, i.e. there exists periods of growth and senescence which are not equal, and that in addition to somewhat gradual changes such as drought induced stress, sudden changes can occur in the vegetation canopy, such as fire, deforestation or crop harvest. As a performance test, the PoLeS is compared with three other smoothing techniques as well as that of the BISE and the TWO techniques.

Profile extraction: The polynomial least squares operation
The premise of data smoothing is that one is measuring a variable that is both slowly varying and also corrupted by random noise. Rather than having their properties defined in the Fourier domain, and then translated to the time domain, PoLeS derive directly from a particular formulation of data smoothing problem in the time domain. PoLeS filters were initially used to render visible the relative widths and heights of spectral lines in noisy chemical spectrometric data.

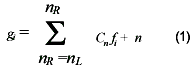
In principle, a digital filter is applied to a series of equally spaced data values fi= f(ti), where ti=to +i for some constant sample spacing and i = …-2, -1, 0, 1, 2, …A digital filter replaces each data value fi by a linear combinationgi of itself and some number of nearby neighbors, (1) Here nL is the number of points used “to the left” or “backward in time” of a data point i, i.e. earlier than it, while nR is the number used “to the right” or “forward in time”, i.e. later or after the data point.

In order to understand the PoLeS, consider the simplest possible averaging procedure: For some fixed nL = nR, compute each gI as the average of data points from fi – nL to fi+ nR. This is sometimes called the moving window averaging and corresponds to equation 1 with constant cn = 1 / (nL + nR + 1). If the underlying function is constant , or is changing linearly with time (increasing or decreasing), then no bias is introduced into the result. Higher points at the one end of the averaging interval are on the average balanced by lower points at the other end. A bias is introduced , however, if the underlying function has a nonzero second derivative. At a local maximum, for example, moving window averaging always reduces the function value. In the spectrometric application, a narrow spectral line has its height reduced and its width increased. Since these parameters are themselves of physical interest, the biased introduced is distinctly undesirable.

Note, however, that the moving window averaging does preserve the area under the spectral line, which is its zeroth moment, and also (if the window is symmetric with nL = nR ) its mean position in time , which is its first moment. What is violated is the first moment, equivalent to the line width. The idea of PoLeS is to find the filter coefficients Cn that can preserve higher moments. Equivalently, the idea is to approximate the underlying function within the moving window not by a constant (whose estimate is the average), but by a polynomial of higher order, typically quadratic or quartic: For each point fi, we least squares fit a polynomial to all nL + nR + 1 points in the moving window, and then set gi to be the value of the polynomial at position i. The value of the polynomial is not used at any other point. Moving to the next point, fi + 1, the least squares process is applied using a shifted window. The process of least squares fitting involves a linear matrix inversion, the coefficients of a fitted polynomial are themselves linear in the values of the data, which would mean that coefficients can be derived which could be applied to different sets of data as some kind of filter coefficients. To derive such coefficients, consider how go might be obtained: By fitting a polynomial of degree M in i, namely ao + a1i + . . . + aMi to the values f-nL . . ., fnR. Then go will be the value of that polynomial at i = 0, namelya0. The design matrix for this problem is

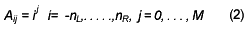
and the normal equations for the vector of aj’s in terms of the vector of fi’s is in the matrix notation.

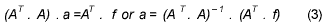
we also have the specific forms

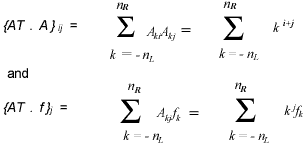
k j fk.Since the coefficients cn is the component a0 when f is replaced by the unit vector en, - nL < n < nR, we have

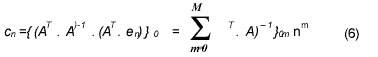
NOAA-AVHRR Pathfinder NDVI 10-day time series data for the year 1984 were taken and were geometrically corrected. 3X3 Sample data different land cover types namely, for Central Africa (desert), Eastern Canada (deciduous), Philippines (two-time cropping), and Central Brazil (tropical) were collected and annual NDV profiles were constructed. Agbu et al (1994) describes the Pathfinder format. The typically noisy profile can be seen in the original data shown in the figure1. The PoLeS algorithm assumes (1) that cloud and cloud shadow and poor atmospheric conditions will usually depress NDVI values (Arino et al. 1991, Simpson et al 2000); (2) that there exists vestiges (relics) of various systematic and data transmissions errors which tend to increase the NDVI values. Lovell et al (2001) had explicitly indicated that the 10-day compositing period (based on the MVC method) did not remove all cloud and spurious high values (e.g. data transmission errors). Other systematic errors include anistropic (describes a medium which has physical properties different in different directions) sources such as the Bi-directional Reflectance Distribution Function (BRDF) (Macmanus 2001). Likewise, scattering within the atmosphere is said to be anistrophic (CCRS, 2002). Similar effects of increased value NDVI due to changes in satellite view angle have been reported (METECH, 2001).

The surface effects such as BRDF and Bi-directional Emission Distribution Function (BEDF) can all be looked at as varying scene brightness that does not indicate changes in the surface type and condition (phenology) but rather the varying sun condition and view geometry of the data. AVHRR and airborne data both share the problems of widely varying scene brightness. Canadian researches have indicated about 30% of the variation in AVHRR based NDVI can be due to sun and view angle effects (Jupp, 1997). Similar anomalies have been found in analyses by Epiphanio et al (1995) and Eastman and Fulk (1993). While the effects of changing view and illumination are sometimes mentioned in studies using AVHRR, the reference is usually made in passing and other disturbance factors are sought to try to explain the anomalies apparent .

In view of the fact that most of the previously proposed NDVI profile extraction methodologies have the intrinsic bias of considering only low frequency NDVI values as noise data and, with the assumption that the surface characteristics are non-isotropic. Previous NDVI profile extraction algorithms also assume that the peaks interpolated from and which conform to the conditions set by the various algorithm (i.e. BISE and MVI) correspond to the absolute values of NDVI curve at those particular points. The PoLeS method, on the other hand, assumes that both high frequency as well as low frequency noise exist in the PAL NDVI data, and should therefore be considered in the interpolation of the NDVI profile.

Pecularities of PoLeS algorithm
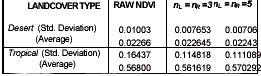
The data for the raw and the filtered NDVI values for the 1984 10-day composite data was are shown in table 1. Figure 1 shows the various results of filtering using PoLeS method. Like, the BISE, MVC MVI and TWO, the PoLeS is also sensitive to the length of the sliding period, a.k.a temporal window or moving window. Two temporal window sizes were tested, where nL = nR =3 and 5. In both window sizes the general interpolated curve is maintained. However, with greater values of the temporal window (e.g. nL = nR =5), there could be observed some substantial smoothing, in which case most of the noise have been removed, albeit it has also smoothed out some of the more important changes inherent in the data. One particular notable effect of the length of the sliding period may be apparent in figure 1.(f) where the inherent changing phenology in the two-crop area was emphasized by the PoLeS filtering procedure. Presuming that the BISE or the TWO method were applied to the same set of data, this valley would not have been detected nor would it be apparent in the profile.

Applying the PoLeS to land cover types which are assumed to have very minimal or ideal absence of change in phenology (i.e. tropical, desert areas) had substantially lowered the overall average comparing the values with the original NDVI data (see table 1) . However, the standard deviation values of the filtered annual data were not changed significantly.

Table 1. Average NDVI and computed standard deviations of two land cover types (i.e. desert and tropical) assumed to have minimal changes in seasonal phenology and the NDVI., as shown by their minimal changes in the data variability before and after applying different temporal window sizes.

Conclusion
The PoLeS provides an alternative method for removing both low and high values from the NDVI profile data. PoLeS made over extensive periods are effective in reducing influences due to clouds and variable viewing conditions, but much like the previous profile extraction methods, the length of the temporal or sliding window affects the smoothness of the entire profile. Longer temporal windows generally smooth out the curve without affecting the overall standard deviation values of the annual NDVI data. A value of the temporal window of 5 (nL = nR=5) substantially provides a good fitting of the NDVI profile. The phenomenon of surface anisotropy due to specific viewing angles and atmospheric conditions can elicit high NDVI values generally in the forward scattering direction (Gutman, 1991). All previous methods, like the BISE, MVC, and MVI will always include and retain spurious high values from data transmission errors and anistropic effects. Whereas, other previous algorithms introduce a bias due to the assumption that a lower values of NDVI are considered only as noise while retaining higher values, the PoLeS does not suffer from such a bias.

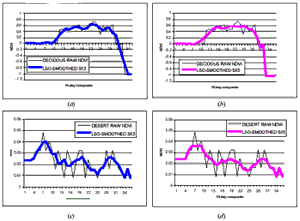
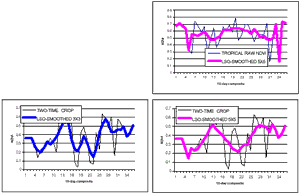
Furthermore, the PoLeS preserves the inherent variability in the NDVI data by preserving the variance of the data as shown by the minimal changes in the value standard deviations.

References

Agbu, P.A., and M.E. James. 1994. The NOAA/NASA Pathfinder AVHRR Land Data Set Users’ Manual. Goddard Distributed Archive Center, NASA, Goddard Space Flight Center, Greenbelt.
Arino, O., Dedieu, G., and Deschamps, P.Y., Determination of satellite land surface reflectances using METEOSAT and NOAA/AVHRR shortwave channel data. International Journal of Remote Sensing, 13, 12, 2263-2287.
Bartholome, E. 1991. Remote sensing and agricultural production monitoring in the Sahelian countries. In Remote Sensing and Geographical Information Systems for Resource Management in Developing Countries, edited by A.S.
Belwrad and C.R.Valenzuela (Dordrecht: Kluwer Academic), pp. 189-214. CCRS, 2000, Correction for Bi-Directional Effects. Canada Centre for Remote Sensing [Online]. Available: http://www.ccrs.nrcan.gc.ca/ccrs/tekrd/rd/apps/em/corr/brdfe.html
Eastman, J.R. and Fulk, M.A., 1992. Time series Map Analysis Using Standardized Principal Component Analysis. ASPRS/ACSM/RT92 Technical papers, Vol.1 Global Change and Education, 195-204.
Epiphanio, J.C., and Huete, A.R., 1995. Dependence of NDVI and SAVI on sun sensor geometry and its effect on fAPAR relationships in Alfalfa. Remote Sensing of the Environment, 51 (3), 351-360. LSO-SMOOTHED 5X5.
Gutman, G.G., 1991, Vegetation Indices from AVHRR: An Update and Future Prospects, Remote Sensing of Environment, 35, 121-136.
Holben, B.N., 1986, Characteristics of Maximum Value Composite Images from Temporal AVHRR data, International Journal of Remote Sensing, 7, 1417-1434. Jupp, D.L.B., 1997. Operational environmental satellite data applications: How the EOC can help achieve them in Australia in CSIRO EOS [Online]. Available: http://www.cossa.csiro.au/pubrep%20/eocwst.htm
Lovell, J.L. and Graetz, R.D., 2001, Filtering pathfinder AVHRR Land NDVI data for Australia. International Journal of Remote Sensing, 22, 2649-2654.
Malingreau, J.P., 1986, Global Vegetation Dynamics: Satellite Observations Over Asia, International Journal of Remote Sensing, 7, 1121-1146.
Mcmanus, J. 2001. Clear-Sky Analysis of the NOAA/NASA Pathfinder AVHRR Land (PAL) 8-Km Data, SCS-CEOSR/GES-DAAC. 7p.
METECH, 2001. Application of Meteorological Satellite Data in Agriculture in [Online]. Available: http://www.metech.org.cn/zjlt/lt_20.html
NOAA, 1990, The Global vegetation Index Users’ Guide, revised October 1990, NOAA NESDIS, National Climate Data Center, Washington, D.C.
Park, J. and Tateishi, R., 1998, Correction of time series NDVI by the method of Temporal Window Operation (TWO), Proceedings of the 1998 Asian Conference on Remote Sensing [Online]. Available: http://www.gisdevelopment.net/aars/acrs/1998/ps2/ps2004.shtml Prentice, K.C., 1990, Bioclimatic distribution of vegetation for general circulation model studies. Journal of Geophysical Research, 95, 11811-11830.
Prince, S.D. and Justice, C.O., 1991, editorial. Coarse resolution remote sensing of the Sahelian environment, special edition, International Journal of Remote Sensing, 7, 1555-1570. Prince, S.D. and Tucker, C.J., 1986, Satellite Remote Sensing of the Rangelands in Botswana. II. NOAA
AVHRR and Herbaceous Vegetation. International Journal of Remote Sensing, 7, 1555-1570. Simpson, J.J. , J. Zhonghai, and J.R. Stitt ,2000. Cloud shadow detection under arbitrary viewing and illumination conditions. IEEE Transactions on Geoscience and Remote Sensing, 38, 972-976.
Taddei, R., 1997, Maximum value interpolated (MVI): a Maximum Value Composite method improvement in vegetation index profiles analysis, International Journal of Remote Sensing, 18, 2365-2370. Wonnacott R.J. and T.H. Wonnacott. Introductory Statistics. John Wiley and Sons. New York 1985. 4 th Ed.
Viovy, N. and Arino, O. and A.S. Belward, 1992, The Best Index Slope Extraction (BISE): A method for reducing noise in NDVI time series, International Journal of Remote Sensing, 13, 1585-1590.