GISdevelopment.net ---> AARS ---> ACRS 2002 ---> Data Processing, Algorithm and Modelling Large area change detection by differencing radiometrically-normalized images Itthi Trisirisatayawong Lecturer, Department of Survey Engineering Chulalongkorn University Tel: (66)-2-218-6659 Fax: (66)-2-218-6653 E-mail: itthi@chula.ac.th Thailand Wallapa Samchimchom Survey Engineer, Department of Lands Tel: (66)-2-984-0959 Fax: (66)-2-503 3430 E-mail: wallapa_s@yahoo.com Thailand Abstract Multi-temporal satellite imageries can be used for change detection. Though simple and intuitive, image differencing technique which is simply done by subtracting pixel brightness values of one image from another can produce false alarms which are areas that changes are indicated while in fact no changes occur. Two major factors causing false alarms are different sun angle and atmospheric conditions and effects from both of which must be eliminated by some pre-differencing process. This paper investigates band-by-band linear regression method to normalize brightness values of a full-scene Landsat TM imagery covering eastern part of Thailand with another co-register close-date 12 year apart Landsat TM scene. The image pair are then differenced and classified by different threshold values to produce change maps which are further checked against ground-observation data for accuracy assessment. As a result, suitable threshold value are determined for large area change detection which can be applied in activities such as environmental monitoring, coastal resource monitoring or urban expansion monitoring. Introduction Change detection is one of major applications of satellite imageries. Basically, areas of change can be identified by taking the difference of pixel value from a pair of co-registered images acquired at different times. In terms of image processing, this simply is the subtraction of one image from another. Because brightness values in each band of a multispectral image have an association with different type of land covers, the change in brightness values over time signify that change in land cover occurs. But in some applications of change detection, the values used in subtraction may be those obtained after some kind of transformation has been performed. For example, the tasseled-cap change in greenness was used to detect crop-type changes and vegetation to nonvegetation changes or vice versa (Fung, 1990). Ideally, the image pair used in change detection should be taken on the same date of different years, the so-called anniversary date. Due to many factors, this may be difficult to achieve and using images of slightly different date are usually the case. Non-surface factors such as atmospheric effects and illumination difference caused by different sun angle can influence pixel’s brightness value so accurate normalization to minimize the effects from non-surface factors is therefore essential. Atmospheric correction schemes which may use the in-situ measurements or pure image-based techniques such as those described in Chavez Jr (1996) and Hu et al (2000) can be used to correct the effects caused by atmospheric factors in each image before taking the difference. However, the most common technique employed in normalization is linear regression using y-intercept and slope parameters (Jensen et al, 1995). The studies on change detection based on differencing radiometrically-normalized images have been performed usually on areas relatively small comparing to the area size covered by a scene of satellite imagery. For example the study site of Fung (1990) was about 280 sq.km whereas in Heo and Fitzhugh (2000) the study area was about 30 km x 30 km or 900 sq.km..Many studies such as forest monitoring, environmental monitoring or coastal resource monitoring have to perform on a large area to see pattern of changes and it is not clear whether linear regression model is suitable in this case. This is because variations of the effects from non-surface factors do not necessarily follow linear model, and the larger the area the more likely deviation from linear model should be the case. Subdivision of large study area into smaller portions, each of which a linear regression is applied, seems to be a solution but this approach may be impractical if many subdivisions are required. Other factors such as time and budget may constrain the use of this method. Another possible approach is to apply a linear regression to the whole study area, provided that the non-surface factors especially atmospheric conditions in the region are known not to change abruptly. This is the approach undertaken by this study. Desctiption of study area and Landsat images The study area is the provinces of Rayong and Chantaburi. The economy of these two eastern provinces depend on agriculture and fisheries. Both provinces are regarded as the country’s orchard, producing top quality of fruits such as durian and mangoesteen. The pattern of land cover is dominated by different type of orchards mixed with rubber plantation, cassava farms, urban areas and many small communities areas. Because of its proximity to Bangkok, Rayong has been developed as an industrial base. A deep-sea port and two industrial estates have caused huge impact on the province. Chantaburi is farther away from Bangkok and less industrialized than Rayong. In recent years, however, the development of tourism and shrimp farming along the province’s coast line have also started making impact on the environment and pattern of landuse. The total area of Rayong and Chantaburi is about 9,890 sq.km. The study area is part of a much larger area (covering upper part of Gulf of Thailand) being mapped by the coastal resource inventory and monitoring project, a long term project sponsored by the Department of Environmental Quality Promotion. The nature of the project demands up-to-date and low-priced data and remotely-sensed images fit well to this demand. Two Landsat 5 TM images of the same path-row (128-51) were used as primary data source for this study. The images were taken on 3 November 2000 and 20 December 1988. The images were rectified, radiometrically normalized, differenced and tested as detailed in subsequent sections. Images Rectification The year 2000 image was rectified to the UTM map plane by a second degree polynomial transformation using ground coordinates obtained from GPS’s precise single-point-positioning (PSPP) methods. The use of GPS PSPP, which can provide coordinate accuracy at around 5 m, to create GCPs (Ground Control Point) for the rectification process was necessary. This is because the most accurate maps covering the study areas are topographic maps at the scale of 1:50,000. Cartographic generalization process such as simplification, exaggeration, and displacement of symbol which are used for the purpose of enhancing the readability have caused positional error which is undesired side effect if the maps are to be used to obtain precise coordinates. Combining errors from map generalization with pointing error and others such as paper shrinking would cause a positional error of more than pixel size and therefore map-derived GCPs were not suitable. Further, most of the 1:50,000 topographic maps in these areas have not been updated for almost 20 years, so many GCPs selected on the Landsat image cannot be located on maps making a GPS campaign to establish GCPs an obvious choice. A total of 17 GCPs were measured by GPS and the RMS error of 0.21 pixel was achieved. The 1988 image was then co-registered to the 2000 image by second degree polynomial transformation using 30 common points. The RMS error of the transformation was 0.20 pixel. The good metric accuracy achieved on both images reassures that ground-truth data located in the field by hand-held GPS, which provides comparatively equal positional accuracy of 10-15 m (0.3 – 0.5 pixel), could be located on the images with minimum ambiguity Radiometric Normalization and image Differencing Radiometric normalization needs targets having the properties of constant reflectors. A constant reflector is the areas which are not covered by vegetation and so any change in brightness values are due solely to non-surface factors. Forty single-pixel targets were selected according to criteria stated in Heo and Fitzhugh (2000). Most developed areas cluster along the coast line making the choosing of normalization targets relatively easy while much lesser targets could be identified in the agricultural-dominant inland areas. As a result, the distribution of normalization targets substantially biases towards the coastal areas as seen in figure 1. However, trying to incorporate more unsuitable targets to compensate the shortfall of the appropriate ones is not a good strategy and since the study is part of the project which pay special attention to map and monitor what are happening along the coast, this situation is considered as a favor given to priority areas. Scatter plots of brightness values in TM band 1 – 4 of the targets is shown in figure 2. In every band, the range of brightness values covered by targets are good and it can be seen that strong positive correlation exist in linear form between brightness values of the 1988 and those of the year 2000 image. The coefficient of determination (R 2 ) ranges between 77.6 % in Band 3 to 84.3 % in Band 4. Statistical test at 95 % confidence interval of the linear correlation coefficient (R) using Pearson critical value of 0.312 (Triola, 1995) concludes that there is a significant linear correlation. 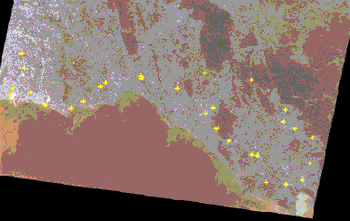Figure 1. Normalizations targets in the bottom half of the year 2000 Landsat 5 image. 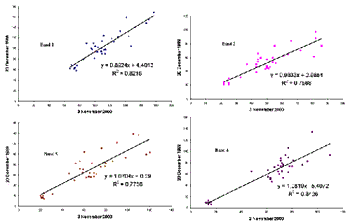Figure 2. Linear regression analysis of TM band 1 – 4. The slope and coefficient parameters determined from least square linear regression were used to normalize the year 2000 image’s brightness values to the year 1988 using ERDAS 8.4 software. The normalized year 2000 image was then subtracted pixel by pixel from the year 1988 image and produced the differenced image whose brightness values are in floating point number. Image resulting from differencing can be classified to produce change image or change map. Theoretically, areas in change maps whose values are greater or lesser than zero are considered as changed but taking into account the factors such as perfect co-registration and normalization cannot be achieved a tolerance is required. A difference image tends to have a histogram that is normal in shape with the peak at or near zero and a long tail extending towards the higher values (Mather, 1999). The mean and standard deviation of the difference image is shown in table 1. Different strategies to choose the suitable threshold exist but an intuitive one would base on the statistical characteristic of pixel values in the difference image. A method suggested by Fung and Ledrew (1988) is to select threshold values at +/- N standard deviation from the mean where N is a small number like 0.1. Accuracy is determined and the threshold value is increased by N for the next round of classification. This is done repetitively and results from each iteration are tabulated for accuracy assessment. The optimal threshold value is the one which provides most accurate result. The method of Fung and Ledrew (1988) is slightly simplified and adopted for this research. The simplification is done by using single threshold value for every band instead of one for each band. The threshold value is set at the increment of 5.0 which is approximately half the average of standard deviations in four bands. Another simplification made is to threshold the difference image from zero rather than from the mean of each band. This is done because otherwise it would be possible and difficult to justify for a pixel having zero value to be classified as ‘change’ if the mean differs significantly from zero. Table 1. Mean and standard deviation of the difference image. Accuracy Assessment One hundred and eighty check points were selected for the accuracy assessment of change detection. The location of these points lie in the narrow strip of about 30 km wide running along the 200 km coast line of Rayong and Chantaburi. To minimize the effect of positional error, each selected locations must cover the area of at least a few pixel. Roughly one third of the ground truth points could be unambiguously interpreted from the year 2000 image and the others were checked in the field. Next, Visual interpretation on the old Landsat image was carried out to determine what these selected point were in the year 1988. However, the majority of the selected locations could not be determined in this way and so the 1:15,000 aerial photographs obtained from the Land Titling project taken in 1990 were employed in the interpretation process. The position of these points together with the information of what they were in 1988 and 2000 were used to construct an Arcview shape file. Finally, another attribute field indicating if change really happened at a point was then derived. 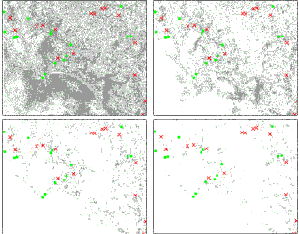For the sake of convenience, the difference image was transformed to the Arcview’s grid format file so that all subsequent work can be carried out in a GIS environment Figure 3. Ground truth locations superimpose on change map produced by different threshold values, above left) 5, above right) 10, low left) 15, low right) 20. With the aid of verified locations, the accuracy of change detection was determined in the following way. The difference image, now in grid-format change map, was classified into two categories of change and no-change using a threshold. Figure 3 illustrates a subarea of the study site with the change areas in grey and no-change areas in white. The known locations were also classified into two categories of change (symbolized as small crosses) and no-change (as small circles). Superimposing the known locations over the classified change map gives a visual clue of how accurate the specified threshold provides. At each location, the change detection is correct if a cross is over a grey area or a circle is over a white area. A cross over a white area is a false alarm or commission error while a circle over a grey area means omission error. An Arcview’s avenue script was developed to facilitate this accuracy determination. Table 2 shows the result. Table 2. Accuracy of change detection. Highest accuracy for each band is highlighted. Threshol d Band # Ground Truth Locations # Correct Detection Accuracy (%) # Commission Error # Omission Error Total Error (%) 5 1 180 128 71.1 50 2 28.9 nbsp; 2 180 136 75.6 41 3 24.4 nbsp; 3 180 129 71.7 51 0 28.3 nbsp; 4 180 111 61.7 48 21 38.3 Threshol d Band # Ground Truth Locations # Correct Detection Accuracy (%) # Commission Error # Omission Error Total Error (%) 10 1 180 132 73.3 45 3 26.7 nbsp; 2 180 130 72.2 35 15 27.8 nbsp; 3 180 128 71.1 49 3 28.9 nbsp; 4 180 106 58.9 37 37 41.1 Threshol Band # Ground Truth Locations # Correct Detection Accuracy (%) # Commission Error # Omission Error Total Error (%) 15 1 180 133 73.4 37 10 26.6 nbsp; 2 180 119 66.1 27 34 33.9 nbsp; 3 180 131 72.8 45 4 27.2 nbsp; 4 180 89 49.4 34 57 50.6 Threshold 20 Threshold Band 1 2 3 4 Band # Ground Truth Locations 180 180 180 180 180 # Ground Truth locations # Correct Detection 132 112 136 78 # Correct Detection Accuracy (%) 73.3 62.2 75.6 43.3 accuracy (%) # Commission Error 30 22 37 27 # commission Error # Omission Error 18 46 7 75 # Omission Error Total Error (%) 26.7 37.8 24.4 56.7 Total Error (%) 25 1 180 129 71.7 24 27 28.3 nbsp; 2 180 102 56.7 18 60 43.3 nbsp; 3 180 131 72.8 34 15 27.2 nbsp; 4 180 73 40.6 18 89 59.4 The experiment shows that most accurate results can be achieved by using band 2 with the threshold value of 5 or band 3 with the threshold value of 20. Comparing to other bands, the use of band 4 results in a consistently less accurate detection, falling below 50 percent once the threshold is set to 15 and over. Between the threshold value of 5 and 20, mixed result is obtained with accuracy increases with threshold in some bands and decreases in others. But the drop of correct detections in every band when the threshold is increased from 20 to 25 indicates that the value of around 20 is the optimal threshold. Overall the experiment demonstrates that large area change detection with the accuracy of around 70 percent can be achieved. Bias in check point selection may play a role in explaining why Landsat TM band 4 yields significantly less accurate result than those obtained from other bands but this is not yet fully understood and is subject to further investigation. Conclusion To really see the pattern of changes, activities such as environmental state monitoring, coastal resource monitoring, crop replacement or urban expansion monitoring are normally performed over large area. Differencing radiometrically normalized images is a simple and intuitive technique that can be used effectively for this purpose. Most experiments so far, however, have focused on areas relatively small comparing to the whole satellite image scene. The result of this research clearly demonstrates that such technique can be used over large area and satisfactory accuracy can be achieved. Further research is being undertaken to determine appropriate spectral band for each kind of change. Another area of investigation is to verify if the same level of detection accuracy can be achieved in the area not well-covered by normalization targets. References Chavez Jr, P.S., 1996. Image-Based Atmospheric Corrections – Revisited and Improved. Photogrammetric Engineering and Remote Sensing, 62 (9), pp. 1025 – 1036. Fung, T., and Ledrew, E., 1988. The determination of optimal threshold levels for change detection using various accuracy indices. Photogrammetric Engineering and Remote Sensing, 54 (10), pp. 1449 – 1454..Fung, T., 1990. An Assessment of TM Imagery for Land-Cover Change Detection. IEEE Transactions on Geoscience and Remote Sensing, 28 (4), pp. 681-684. Heo, J., and Fitzhugh, T.W., 2000. A Standardized Radiometric Normalization Method for Change Detection Using Remotely Sensed Imagery. 66 (2), pp. 173-181. Hu C., Carder K.L., and Muller-Kargen F.E., 2000. Atmospheric Correction of SeaWiFS Imagery over Turbid Coastal Waters: A Practical Method. Remote Sensing of Environment, 74, pp. 195 – 206. Jensen, J.R., Rutchey K., Koch M.S., and Narumalani S., 1995. Inland Wetland Change Detection in the Everglades Water Conservation Area 2A Using a Time Series of Normalized Remotely Sensed Data. Photogrammetric Engineering and Remote Sensing, 61 (2), pp. 199-209. Mather, P.M., 1999. Computer Processing of Remotely-Sensed Images. John Wiley & Sons, pp. 114 – 115. Triola, M.F., 1995. Elementary Statistics. Addison-Wesley, New York, pp. 476 – 482.