GISdevelopment.net ---> AARS ---> ACRS 2002 ---> Land Use/Land Cover Integrated ANN Modelling for assesment of Runoff due to Land-Use change using Remote Sensing and GIS Dr. Madhav Narayan Shrestha Assistant Manager, Nepal Water Supply Corporation, Kathmandu, Nepal Tel: +977-1-271429, Email: http://www.gisdevelopment.net/aars/acrs/2002/luc/madhavnarayan@yahoo.com Abstract An integrated artificial neural network (ANN) model considering spatial variability using remote sensing, and GIS is developed to assess the changes in runoff value due to land use change in a hydrological basin. Kathmandu Valley basin, Nepal, is chosen as a basin of case study. It is found that the average daily monsoon flow is increased by 12% for 9% deforestation and 17% urbanization. Peak flow value in the basin during monsoon season is found increased by 14%. It is found that the percentage change in runoff due to land use change is almost constant for different land use irrespective of the rainfall pattern and time of occurrence. The performance of the network in training and validation using Feed forward back propagation network (FFBPN) model to predict the runoff from the land-use, soil moisture and rainfall is found to be quite satisfactory when compared to Recurrent Neural Network (RNN). The total runoff values for different percentage of urbanization predicted by Distributed Hydrological Model (DHM) and FFBPN model are found to be close than that of RNN model. If the land-use change and climatic data of a basin are available for sufficient periods covering all extreme conditions , the FFBPN can be used for estimation of flows for ungaged periods. During low flow period, RNN models underestimated the runoff more compared to FFBPN. RNN model will be more appropriate for high flow condition. The study clearly demonstrated that integration ANN model with remote sensing and GIS, and spatial distributed model provides a powerful tool for assessment of the hydrological effect due to land use changes. Introduction There has been a growing need to quantify the impacts of land use changes on hydrology from the point of minimising potential environmental impacts. The conventional methods of detecting land use changes are costly, low in accuracy. Remote sensing because of its capability of synoptic viewing and repetitive coverage, provides us eful information on land use dynamics. With the development of GIS and remote sensing techniques, the hydrological catchment models have been more physically based and distributed to enumerate various interactive hydrological processes considering spatial heterogeneity. The purpose of this study is to integrate ANN model for assessment of runoff due to land-use change. The non-linear response of a watershed (in terms of runoff) to rainfall events makes the problem very complicated. In addition, spatial heterogeneity of various physical and geomorphologic properties of a watershed cannot be easily represented in physical models. The rainfall-runoff relationship is one of the most complex hydrologic phenomena due to the tremendous spatial and temporal variability of the watershed characteristics and unpredictable rainfall pattern. ANN models are capable of mapping this non-linearity. System for Study The system considered for the study is Kathmandu Valley basin. The valley is a roughly circular bowl shaped intramontane basin, of 651 km 2 and lies between 27° 32' N to 27° 49' N and 85° 11' E to 85° 32' E. Bagmati river is the main river originates from north hill and flows towards south-west and forms a typical centripetal drainage system. It passes through Chovar gorge, which is the only outlet of the basin.. The maximum and minimum temperatures are 35 0 C and -2.5 0 C respectively. The rainfall occurs about 80% of the total annual rainfall during the months of June to September. The average annual rainfall in the basin is 1600 mm. The basin is divided into 14 subbasins considering topography and is shown in Fig.1. Fig.1. Subbasin M ap of Kathmandu Valley.Fig.Ar ea ( %) The land use map for the year 1978 is derived from topomaps using Arc/Info. Digital images for 1984 (Landsat TM), 1990 (Landsat TM) and 1996 (Landsat TM) are used to derive the land use maps by digital image process. Visual image interpretation of satellite data is carried out using an interpretation key generated through field survey and verifications. The ground checks are made for confirming the land use units. The spatial database containing information on land use, soil type, topography, hydraulic characteristics and meteorological information is created using Arc/Info. The hydrological soil group (HSG).map is derived from the soil map whereas subabsin boundary map is derived from the drainage map. The Thiessen Polygon map is derived using available rain gauge stations. In the study area, the forest (mountainous) area is about 30% of the total basin area having slop range from 20 to 30%, and remaining area (70%) is having average slope of 0 to 4%. The map of newly proposed plan with 27 new settlements, outer ring road and connecting radial roads (KVTDPIC, 1998) is derived as future plan scenario. The future development consists of 18-km 2 area of settlements, 66 km outer ring road around the foothills, which covers mostly agricultural land and 20.25 km connecting radial road. Considering the development of existing built-up pattern on the either side of ring road, 110m widths the settlement area along the outer ring road and 95 m width along connecting road are considered as future development. The daily and monthly rainfall record of 9 raingauge stations for period 1965 to 1996 are used. The daily data for five stream gauging stations, namely Chovar, Gaurighat, Buddhanilkantha, Sundarijal and Tika Bhairab are collected. Some missing records are filled in considering the correlation structure with other stations. The correlation coefficients are found in between 0.87 and 0.97. Methodology Development of Hydrological Model: The method for evaluating the change in runoff value due to land use changes can be implemented by integrating remote sensing, GIS and ANN Model. In this study, the computational elements of ‘Hydrological Similar Units’ (HSU) (Ott et al, 1991) are considered with accurate mapping of land-use at micro level using remote sensing and GIS. Three-dimensional physiographic heterogeneity in terms of topography, soil and land use can be grouped together into associations. These associations are defined here as Hydrological Similar Units. HSUs are areas with same land use, same pedo-topo-geological conditions controlling their unique hydrological dynamics. The widely accepted, the SCS-CN technique is adapted here to compute the runoff from the several HSUs of the basin for the given rainfall. The runoff from each individual HSUs are then routed and the total runoff resulted from the basin is computed for the given rainfall using Muskingum routing method by HEC-I model. Land use, hydrologic soil group (HSG) and slope coverages are overlaid using Arc/Info to delineate the HSUs. Appropriate curve numbers (CNs) are assigned to each HSU considering antecedent moisture conditions (AMC). Then the direct runoff values from each HSU are estimated using SCS-CN method for rainfall events. Effectof land use changes are evaluated for different periods by quantifying the runoff. The changes in land use are evaluated by accounting the HSU distribution over the entire area for different periods and which in turn, gives the changes in CN over the period considered. Development of ANN model: The relationship between the changes of the runoff values for the change in rainfall was found to be non-linear for different land-use (Shrestha, 2001) For efficient mapping of non-linear rainfall-runoff pattern, the artificial Neural Network (ANN) models are developed and these neural networks can be used as a decision-making tool to assess change in runoff due to different land-use changes. Two types of the ANN models namely Feed forward error back propagation network (FFBPN) (Rumelhart et al, 1986) and Recurrent Neural Network (RNN) as feedback ANN (Elman, 1990) are adapted. These models are developed separately for each subbasins of the study area. The training of the model is accomplished by providing inputs to the model, computing the output and adjusting the interconnection weights until the desired outputs are obtained. When the training is completed, the weight for each interconnection is known and remains fixed for the particular network. The network architecture that resulted in the minimum error over the training epochs is adopted as the optimal architecture. All the input data are normalized. Using optimum network architecture, the ANN models are trained for given input and output sets separately. The modeled output values are then compared with target output. The values are then examined by 95 % level of confidence. To check the scatter of the values, þ10 % deviation band is used. Final weights and bias values calculated during training phase for the network are used for validation phase. The validation involves evaluating the network performance on a set of test problems that were not used for training. The models with defined architecture during training are run for va lidation separately for all the subbasins. The output is compared with target for each subbasin. All sets of monthly-normalized output (runoff) from each ANN models (FFBPN and RNN) designed for the subbasins are considered as input set for integrated ANN model for the entire basin as shown in Fig.2. R1i is monthly rainfall input during ith month to ANN1, which is formulated, for subbasin 1. Similarly SM1i is average moisture condition and L1k is percentage land-use of kth type for subbasin1. Two statistical criteria, namely, root mean square error (RMSE), and model efficiency (R2) (Nash and Sutcliffe, 1970) are employed to measure goodness of fit. These criteria are applied to the model both for training and validation phases. The training parameters are the maximum number of training epochs, error goal, the learning rate, and the momentum factor. The error goal is taken as 0.2 in this study. The error gradient and sum square error are observed over the parameters. RNN is run separately for all subbasins with different hidden neuron numbers..Input Parameters: In the model, there are six inputs namely monthly rainfall, average soil moisture index, and percentage of four major land-use types (forest, agriculture, settlement and pastureland), and only one output as monthly runoff. There are seven types of data sets namely (i) monthly runoff observed from land-use of 1978 (LU1), 1984 (LU2), 1990 (LU3) and 1996 (LU4), (ii) monthly runoff due to superimposed rainfall pattern of 1978 on LU2, LU3 and LU4, (iii) monthly runoff due to superimposed rainfall pattern of 1978 and 1996 on land-use of future plan scenario, (iv) monthly runoff due to superimposed rainfall pattern of 1978 on land-uses after assumed deforestation of 5, 10, 15, and 20%, (v) monthly runoff due to superimposed rainfall pattern of 1978 on land-uses after assumed urbanization of 5, 10, 15,and 20%, (vi) monthly runoff due to superimposed rainfall pattern of 1978 on land-uses after combined deforestation and urbanization of 5, 10,15 and 20 % on upstream subbasin, and (vii) monthly runoff due to superimposed rainfall pattern of 1978 on land-use after combined deforestation and urbanization of 5, 10,15 and 20 % on downstream subbasin. Thus the total numbers of input sets are twenty-five. Each set has 12 subsets of data Twenty-two sets are considered for model training and three sets for validation. 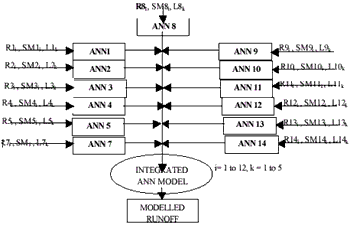Fig.2. Schematic Representation of Integrated Artificial Neural Network for Kathmandu Valley Basin Testing or validation sets are of LU3 with rainfall of year 1990, LU4 with rainfall of year 1996 and future plan scenario with rainfall pattern of year 1996. Thus the total number of input data set for training each subbasin is 264 and 36 for validation. All subbasins have six inputs and subbasins 13 and 14 (Khasyang khusung and Gakhu khola) have five inputs. The percentages of land-use categories for each subbasin are calculated from land-use map of respective years. The average soil moisture index is estimated by taking average of daily antecedent moisture condition estimated according to SCS method (SCS, 1985). The index values are taken as integer after rounding the average value, i.e. 1,2 and 3 for AMC I, II and III respectively for all the days of the month. The model is applied for new set of assumed urbanization of 3%, 18% and 30%. Rainfall pattern of 1978 is superimposed to determine the runoff from these urbanized land-uses. The changed land-use is then overlaid with soil map. HSUs are delineated using Arc/Info after carefully study of possible surrounding area of each HSU for land use change. Overlaying with Thiessen polygon map, the rainfall depth is computed for each HSU. The runoff at outlet of subbasins and outlet of the basin are calculated for three different sets of urbanization by DHM (Shrestha, 2001). The new input sets are used in both ANN models for each subbasin. Using weight and bias matrix of the trained model, the normalized outputs are obtained from individual subbasins ANN model separately. Then these are taken as input in integrated ANN models. Analysis of Results There are four types of HSG, 7 types of land use and five range of slope in the study area. Considering different combinations, twenty-five types of HSUs are derived (Mohan and Shrestha, 2000). HSU type 11 and 15 are not found in the area. Total numbers of HSUs derived are 1119, 1291, 1375 and 407 for 1978, 1984, 1990 and 1996 respectively. The minimum delineation of area observed is of 8 m 2 . The calculated daily runoff values at the outlet of the basin are found close with observed daily runoff during monsoon season and slightly lower during non-monsoon season. The monthly average rainfall over the basin is calculated with Thiessen coefficients derived from Thiessen Polygon coverage. The summation of product of HSU area and CN is divided by the total basin area to calculate three types weighted CN as per AMC. The weighted CNs are 44.87, 61.41 and 76 for the year 1978, 45.17, 61.78, 76.47 for year 1984, 47.66, 64.61, 78.99 for year 1990 and 47.83, 64.8 and 79.2 for year 1996 for AMC I, II and III respectively. Percentage area and distribution of each HSU for different years are shown in Fig.3. 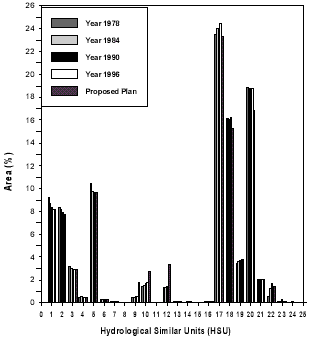Fig.3. 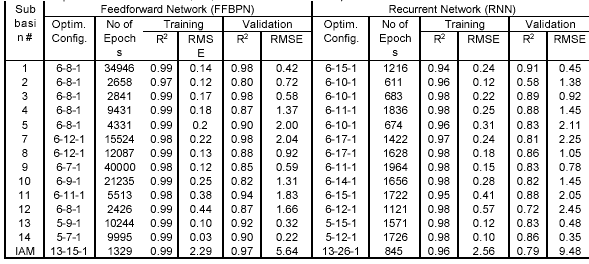Distribution of Hydrological Similar Unit (HSU) for estimated Defferent Landuses Models In this work, the rainfall values occurred in year 1978 are assumed to be occurred on year 1984, 1990 and 1996, to quantify the change in runoff production due to land use change. The changes in the CN values and the changes in the runoff values are then assessed by the difference in runoff values produced by the same rainfall on different land use. The land use change is accounted by evaluation of change in CN from 1978 to 1996. Comparing between 1978 and 1996, the weighted CN for the month of June was found to increase by 3 (6.6%) for AMC I, 3.4 (5.5%) on the month of August for AMC II and 3.2 (4.2%) on the month of September for AMC III. The peak runoff is increased in year 1996 by 3.32 m 3 /s (9.4%) on the month of June, 5.02 m 3 /s (6.5%) on the month of August and 2.305 m 3 /s (5.3%) on September. In sub-basin level, the most change in CN is observed at Gundu sub-basin (12.7%) and the corresponding increase in runoff is 18.8%. The weighted CNs due to future development are increased to 49.04, 65.604 and 79.56 for AMC I, II and III. The same rainfall values (as in 1978) are superimposed on the land use of future scenario to evaluate the effect of the land use change on runoff production. The peak runoff values are found to increase by 4.44 m 3 /s (12.5%), 5.71 m 3 /s (7.4%) and 1.624 m 3 /s (3.7 %) for AMC I, II, III respectively compared with that of year 1978. The corresponding CNs are found to increase by 9.3%, 6.8 % and 4.7 %..The modeled outputs by FFBPN and RNN are compared with target output for each subbasin. The plotting of the results of output for training and validation with 95% confidence level and þ 10 % deviation lines for all models are checked. Most of the points are with in confidence level. In training phase both FFBPN and RNN models for all subbasins indicate very high model efficiency (R 2 ). RMSE values obtained are less than 0.4 for all subbasins except subbasin 12 as presented in Table 1. In validation phase, R 2 values resulted from FFBPN are more than 0.9 for subbasins 1,3,5,11,13 and 14, and ranges from 0.8 to 0.9 for other subbasins whereas for RNN models, R 2 values are found in between 0.8 and 0.9 for all subbasins except subbasin-2 and 12. For integrated ANN model (IAM), the number of input neurons is thirteen and the number of output neuron is one. After several trial and error, the optimum architecture for the basin using FFBPN is found for S1 = 15 with 1329 epochs. Modeled output values are compared with target outputs and the resulting RMSE and R 2 are found as 2.29 and 0.99 respectively (Table 1). During validation RMSE and R 2 are found as 5.64 and 0.97 respectively. The most of the points plotted for modeled and target outputs are found within the confidence level. Using RNN model, the optimum architecture for the basin is found for S1equal 26 with 845 epochs after several trials. R 2 and RMSE values during training are found to be 0.96 and 2.56 respectively. During validation R 2 and RMSE are found as 0.79 and 9.48 respectively. Over all, the FFBPN models resulted in high performance and model outputs are within 95 % confidence level for both training and validation phases. RMSE values are found less in training phase compared to validation phase (Table 1). In all the subbasins, the number of epochs required to train the RNN model are less compared to FFBPN. The total runoff values from different percentage of urbanization (application set) calculated by GIS based DHM and FFBPN models are found close than that of RNN model as shown in Fig 4. RNN model overestimated the total runoff when compared with FFBPN model. Most high runoff values are captured and reproduced by the RNN models during training. Thus during low flow period, RNN models underestimated the runoff more compared to FFBPN and resulted in less R 2 as well as large RMSE value. 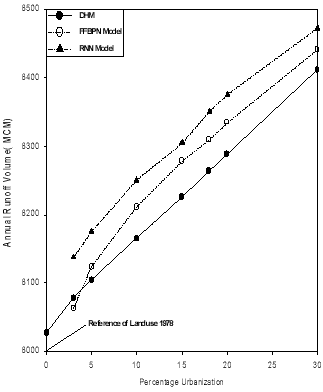Fig.4. Comparison of Annual Runoff Volume by Hydrological Model and ANN for different Urbanizations Table 1 Optimum ANN architecture, R2, RMSE and Number of Epochs for subbasins Conclusions The calculated storm runoff volumes are compared with observed runoff volumes for different storm events of different years and found to be very close to that of observed volumes with difference of less than 2.2 %. It is found that the percentage change in runoff due to the land-use change is almost constant for different land-use irrespective of the rainfall pattern (different years) and time of occurrence (pre monsoon, monsoon and post monsoon). For the study area, it is found that the average daily monsoon flow is increased by 12% when there is 9% deforestation and 17% urbanization and the peak flow value is found increased by 14 %during monsoon season. The peak runoff value is found to be increased by 20 % in subbasin 2 although the equivalent monthly rainfall depth is observed decreased by 3%. The performance of the network in training and validation using FFBPN model to predict the runoff from the land-use, soil moisture and rainfall is found to be quite satisfactory when compared to the performance of RNN. The total runoff values for different percentage of urbanization predicted by DHM and FFBPN model.are found to be close than that of RNN model. If the land-use change and climatic data of a basin are available for sufficient periods covering all extreme conditions, the FFBPN can be used for estimation of flows for ungauged periods. Most of the high runoff values are captured and reproduced by the RNN models. During low flow period, RNN models underestimated the runoff more compared to FFBPN and resulted in less R 2 as well as large RM SE value. RNN model will be more appropriate for high flow condition. Thus it can be concluded that the FFBPN is more suitable than the RNN model for predicting the runoff considering land-use, soil, and rainfall. It is concluded that the integrated ANN models considering spatial variability through Hydrologic Similar Units (HSU) using GIS and Remote Sensing is a powerful tool for assessment of the hydrologic effect due to land-use changes. References Elman, J.L. (1990) Finding structure in time, Cognitive Science, 14, 179-211 Kathmandu Valley Town Development Plan Implementation Committee (KVTDPIC) (1998) Map and Plan, unpublished. Nash, J.E., J.V. Sutcliffe (1970) River flow forecasting through conceptual models Part I – A discussion of principles. Journal of Hydrology. 10, 282-292 Ott, M., Su, Z., Schumann, A.H. and Scultz, G.A. (1991) Development of a distributed hydrological model for flood forecasting and impact assessment of land use change in the International Mosel river basin, Proc. of Vienna Symposium, Aug-91, 183-184. Rumelhart, D.E., G. E. Hinton and R. J. Williams (1986) Learning internal representation by error propagation, Parallel Distributed Processing, Vol. 1: foundations, D. E. Rumelhart and J. L. McClelland, eds, MIT Press, Cambridge, Mass Shrestha, Madhav Narayan (2001), Assessment of Hydrological Changes due to landduse modification, Ph.D. Thesis, India Institute of Technology, Madras. S.Mohan and M.N. Shrestha (2000),’Evaluation of Effects of Land-use changes by Distributed Hydrological Model using Remote Sensing and GIS’, Proceeding of 12 th Congress on the Asia and Pacific Regional Division of International Association for Hydraulic Engineering and Research, Bangkok, 13-16 Nov. 2000, Vol. III, 1093-1103 Soil Conservation Service (SCS) National Engineering Handbook (1985) NEH- Section 4: Hydrology. Chapter 4, Soil Conservation Service, USDA, Washington D.C.