GISdevelopment.net ---> AARS ---> ACRS 2004 ---> Data Processing: Data Fusion Mathematical Models of Trees by Fractal Nana MAYUZUMI, Mayumi ISHIKAWA, Susumu OGAWA Faculty of Geo-Environmental Science, Rissho University 1700 Magechi, Kumagaya, Saitama 360-0194, Phone:(81)-48-539-1652 Facsimile:(81)-48-539-1632 JAPAN Email: 031w00135@ris.ac.jp ABSTRACT Vegetation and tree models are required for monitoring vegetation with remote sensing in various fields. This research aimed at illustration of complicated tree growth process with fractal models. Fractal tree and bifurcation-type tree models were constructed as a mathematical model, and their fractal dimensions were compared natural trees. Consequently, a branch-type tree model looked like real trees, while fractal trees performed like real tree growth. Moreover, tree models showed similar fractal dimensions to real trees in photographs. These trees expressed by simple models would be expected for monitoring vegetation in time series. 1. INTRODUCTION In global environment, modeling of vegetation has become very important. Since the monitoring error is large, the observation by remote sensing requires its improvement. Therefore, construction of mathematical models for vegetation growth process was attempted: trees, a paddy field, and an agricultural field as a model. Especially tree growth models were showed. In order to draw trees by the mathematical model, two conflicting assumptions, "trees have no self-similarity" and "trees have self-similarity", were introduced. Fractal tree and bifurcation-type tree models were calculated and the forms of complicated trees were illustrated. If a tree is expressed by fractal dimension, the improvement in accuracy is expected for growth simulations for forest and the biomass estimate of environmental monitoring. 2. METHOD 2.1 OBJECTIVE AREA Modeling was aimed at the trees in the Musashi-Kyuryo National Government Park located in Namegawa, Saitama. 2.2 CALCULATION OF FRACTAL DIMENSION FOR TREES In this research, the fractal dimension was obtained with the box counting for photographs and models (Takayasu, 1986). First, photographs of the trees were transformed into binary digit images. The logarithm of a pixel size (resolution) was taken along a horizontal axis, while the logarithm of pixels which overlapped the objective figure along vertical axis. The gradient of the regression line for these plots becomes a fractal dimension with the minimum square method. 2.3 MODEL CONSTRUCTION In this research, the model using the fractal figure was called fractal trees. The branch development was called a bifurcation-type tree model. 2.3.1 ALGORISM METHOD OF FRACTAL TREES Fractal trees are generated as an internal self-similarity set and a self-similarity set combining reduction, rotation, parallel, and symmetrical mappings (Ishimura, 1990). 2.3.2 ALGORISM OF TWO-DIMENSIONAL BRANCH TYPE TREES (1) Number of branching: 0 to 3 The probability of occurrence of each branch was assumed as right branch, 78 %, left branch, 78 %, the same direction, 52 %. 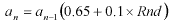(2) Length of branch In the case of the branch extended left and right: where an is the length of the n-th branch and Rnd is random numbers with 65% to 75% of the length before branching. 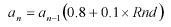In the case of the branch extended the almost same direction as the former branch before branching: where Rnd is random numbers with 80% to 90% of the length before branching. 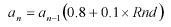(3) Angle at a branch (direction) In the case of the branch extended left and right: Its direction changes 0.3 rad to 0.5 rad to the branch before branching. 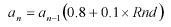In the case of the branch extended the almost same direction as the former branch before branching: Compared with the branch before branching, direction changes -0.05 rad to 0.05 rad. The fractions of the above parameters were given by random numbers. 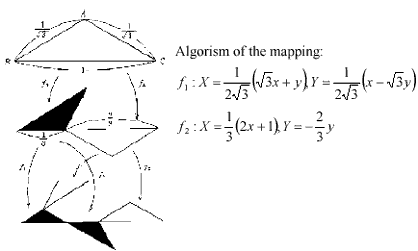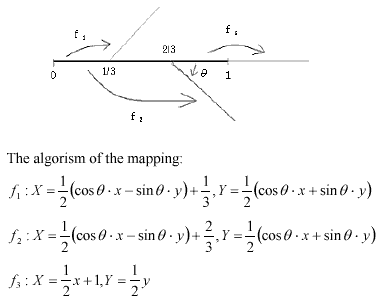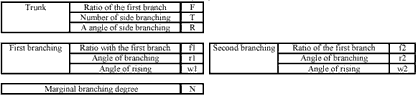Figure 1 Two reduction mappings of the tree model generated as a self-similarity set Figure 2 Mappings of the tree model generated as an internal self-similarity set 2.3.3 THREE-DIMENSIONAL BRANCHING The input parameters were defined as shown in Table 1, and the first trunk was set up. Next, from the first branch, the lengths and angles of side branching were calculated and drawn (Fuchigami, 1992). Table 1 Input parameters 3. RESULTS AND DISCUSSION The bifurcation-type tree model looks like real trees more. The model trees similar to trees in a photograph also showed a near fractal dimension. In the growth model, the fractal trees performed in the nearer motion. This suggested statistical self-similarity in trees. The bifurcation-type of three-dimensional models with branch rules generated various kinds of tree shapes with the arbitrary input parameters. On the other hand, various trees can be displayed by a bifurcation-type of two-dimensional models with random numbers. Probably, two-dimensional model would generate a tree shape by the input parameters. 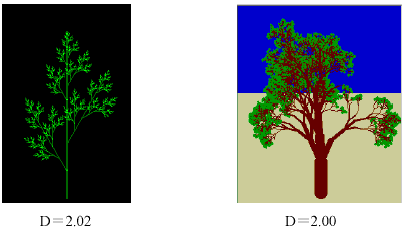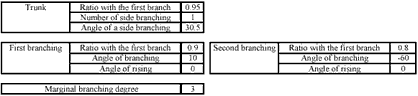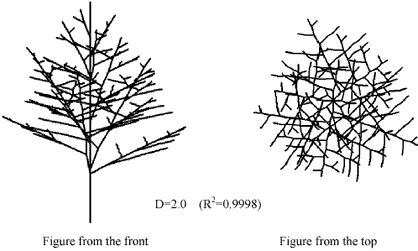Figure 3 Internal self-similarity fractal trees and two-dimensional branching model Figure 4 Self-similarity fractal trees Table 2 Branching conditions of a laurel tree model Figure 5 Photograph of a laurel tree Figure 6 Model of a laurel tree 4. CONCLUSIONS In this research, two hypotheses "trees have no self-similarity" and "trees have self-similarity", introduced two kinds of tree models. The factor which determines the form of trees is branching rules in each tree and the self-similarity in partial modification of trees formation. REFERENCES Takayasu, H. 1986. Fractal, Tokyo, pp. 5-20. Ishimura, S. and Ishimura, S. 1990. Fractal mathematics, Tokyo, pp. 148-254. Fuchigami, K. 1992. CG, Form and Fractal, Tokyo, pp. 36-40.