Application of Singular Spectrum Analysis (SSA) for the Reconstruction of Annual Phenological Profiles of NDVI Time Series Data

Application of Singular Spectrum Analysis (SSA) for the Reconstruction of Annual Phenological Profiles of NDVI Time Series Data

Jose Edgardo L. ABAN
Department of Science and Technology
Gen. Santos Ave., Bicutan Tagig, Metro Manila, Philippines
Tel: + 632-837-2071 to 80 loc. 2100-2109 Fax:+632-837-3168
Email: jelaban@dost.gov.ph

Ryutaro TATEISHI
Center for Environmental Remote Sensing (CEReS)
Chiba University
1-33 Yayoi, Inage, Chiba-ken, Japan
Tel: +81-43-290-3965 Fax: +81-43-290-3857
JAPAN
Email: aban@ceres.cr.chiba-u.ac.jp

ABSTRACT
The Singular Spectrum Analysis (SSA) is proposed as an alternative novel technique used to reduce noise in the Normalized Difference Vegetation Index (NDVI) time-series annual phenology profile from the Advanced Very High Resolution Radiometer (AVHRR) data. The SSA preserves more valuable elements of the NDVI profile based on data-adaptive basis functions. This paper describes a detailed investigation into the suitability of the SSA for NDVI profile reconstruction. The ability of the SSA to decompose the time series into several principal components, distinguish between the main signal and noise, and subsequently reconstruct the original time series through the use of reconstructed components (RC) are demonstrated in this study.

INTRODUCTION
Since 1982, the National Oceanic and Atmospheric Administration’s (NOAA) Advanced Very High Resolution Radiometers (AVHRR) has provided daily Earth observations. From these data, NDVI profiles have been built and compiled through the years. Such multi-annual profiles data have been used to monitor primary production (Prince and Tucker, 1986; Fung et al., 1987), to study the dynamics of major biomes (Malingreau, 1986), for land cover classification (Townshend et al., 1991), and for estimation of crop yield (Bartholome’, 1991). Changes in the NDVI derived from AVHRR data are usually indicative of changes in the surface conditions, most predominantly changes in vegetation. However, there are other extrinsic factors that cause changes in the overall NDVI profile, among which are cloud contamination, atmospheric variability and bi-directional effects (Gutman, 1991; Tucker and Sellers, 1986; Justice et al., 1991; Soufflet et al., 1991; Simpson and Stitt, 1998); these changes are usually considered as undesirable noise in vegetation studies. A widely used method to reduce this noise is the Maximum Value Composite (MVC) technique proposed by Holben (1986) and Prince and Justice (1991). In spite of corrections, the data still contain unwanted variation or “noise” (Gutman, 1991; Tucker and Sellers, 1986; Justice et al., 1991; Soufflet et al., 1991; Simpson and Stitt, 1998).

In this study we explore a relatively new technique called the Singular Spectrum Analysis (SSA). The SSA is similar to an extensively used technique of PCA, whereby it undertakes a linear transformation of a set of image bands to create a new band set with images that are uncorrelated and are ordered in terms of the amount of variance explained in the original data (Johnston, 1980; Mather, 1987, ). whereby the data is decomposed into a set of uncorrelated eigenvectors. The SSA was developed independently by Broomhead and King (1986a, 1986b) and Danilov and Zhigljavsky (1997). SSA is a nonparametric method and assumes no specific model of the process being analyzed. Unlike previous methods of NDVI profile extraction, it uses data-adaptive basis functions, the lag-covariance matrix, rather than threshold limits, or the pre-determined measures of central tendency (i.e. mean, median, or mode), which are basically non-adaptive techniques. Though numerous studies have employed the SSA technique in a variety of environmental as well as econometric applications, the method has never been applied on the derivation of the NDVI profile, for which this present study aims to demonstrate.

1. METHODS

1. 1. Profile Extraction: The Singular Spectrum Analysis (SSA)
The method of SSA is a relatively new technique, and is sufficiently effective and comparative with numerous smoothing techniques (Percival et al., 1993 , Theiler et al., 1992; Kaplan and Glass, 1992). Moreover, in certain cases forecasting the system evolution on its basis gives much more reliable results in comparison with the other known algorithms (Casdagli, 1989; Danilov et al., 1997; Deppish et al., 1991; Murray, 1993; Cao et al., 1995; Keppenne and Ghil, 1992, 1993, 1994, 1995).

The SSA is usually regarded as a method of identifying and extracting oscillatory components from the original time series (Yiou et al., 1996; Ghil and Tarrico, 1997; Fowler and Kember, 1998). It is also used in particular tasks, such as detection of “change-point” in time series (Moskvina and Zhigljavsky, 2002a, 2002b); “extraction of signal from noise”, and smoothing (Golyandina, 2001). This current study is a demonstration of the power of SSA in doing the aforesaid tasks. Filtering “noisy” data using SSA have been performed by Allen et al. (1996, 1997) and Vautard et al. (1992) on earth’s global mean temperature; and on the El Niño-Southern Oscillation (ENSO) (Mann and Lees, 1996).

Suppose that we have a time series x of length N. Suppose that we choose some aximum lag M and compute the M X ..M lag autocovariance matrix,

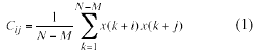
If we do an eigenanalysis of this covariance matrix, we will obtain temporal structures that explain the maximum possible amount of the temporal autocovariance on an interval of measure M. The eigenvalues will be the amount of covariance in time explained y each eigenvector. You can then reconstruct the time series at any point n, by expanding the data in the basis set of eigenfunctions.

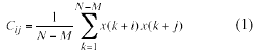
where n=i+j, ek ( j) is the jth element of the kth eigenvector, and ak (i) is an expansion coefficient for the kth eigenvector beginning at the point i.

1.2. Application on NOAA-AVHRR Pathfinder data
NOAA-AVHRR Pathfinder NDVI 10-day time series data for the year 1984 are considered in this study and were geometrically corrected. Sample data of 3X3 pixel size of different land cover types namely, for Africa/Saharan (desert), Eastern Canada (deciduous/boreal), Philippines (two-time cropping), and Central Brazil (tropical) were collected and annual NDVI profiles were constructed. Agbu et al. (1994) describes the Pathfinder format. By default, we choose the lag value M < [N/2+1] , which is equivalent to 17.

The typically noisy profile can be seen in the original data shown in the Figure 1. The SSA algorithm assumes (1) that cloud and cloud shadow and changing atmospheric conditions (such as the persistence of clouds in images) will usually depress NDVI values (Ariño et al,. 1991, Simpson et al., 2000); (2) that there exists vestiges (relics) of various systematic and data transmissions errors which tend to increase the NDVI values.

2. RESULTS AND DISCUSSION
The SSA is not dependent on the sliding period or the moving window as do previous NDVI profiling techniques. Further, the technique does not depend on the use nor determination of a threshold, again another set back of previous techniques except those that have employed Fourier-based techniques. SSA is nonparametric and assumes no specific model of the process being analyzed.

Figure 1 shows the original and reconstructed (“SSA-filtered”) NDVI profiles for various landcover types. The SSA uses data-adaptive basis functions, the eigenmodes of the lag covariance matrix, rather than fixed sines and cosines (Ghil and Tarrico, 1997). By doing so, a box-car or seesaw-shaped oscillation can be represented by a single pair of eigenmodes that capture the basic periodicity, rather than necessitate the many overtones appearing in methods with fixed basis functions.

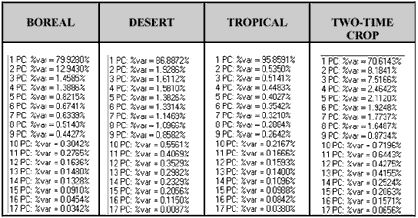
Table 1. Eigenvalues of PC 1 to PC 17 of the different landcover types

Table 1 provides a summary of eigenvalues for each of the landcover types tested in the study. Signal and noise separation may be obtained by plotting these singular values, called the “eigenvalue spectrum”. In decreasing order, one can distinguish an initial steep slope, which represents the signal, and a (more or less) “flat floor”, representing the noise level characterized by lower values (Vautard and Ghil, 1989; Kumaresan and Tufts, 1980; Pike et al., 1984). For the boreal dataset, the flat floor starts from PC 3 to PC17; PC2 to PC17 for desert and tropical datasets; and PC4 to PC17 for two-time crop landcover types.

The reconstructed components (RCs) have the property of capturing the phase of the time series in a well-defined least squares sense and can be superimposed in the same time scale. No information is lost in the reconstruction because the sum of all individual reconstructed components gives back the original time series (Ghil and Vautard, 1991; Vautard et. al, 1992).

The PCs which represent the “flat floor” are excluded from the reconstruction process because these PCs basically represent noise. Partial reconstructions (which actually represent the “true signal”) are obtained by summing the variability of PCs above the “flat floor”, and which are associated with the leading eigenelements and the quasi-periodic behavior isolated by them. Hence, we are left with the following PCs used for the reconstruction of the: boreal, PC1 and PC2, with a summed percentage variance (SPV) of 92.871%; desert, PC1 only with SPV of 86.8872%; tropical, PC1 only with SPV of 95.8591%; and two-time cropping , PC1, PC2, and PC3 with SPV of 86.315%.

It is noteworthy for the reconstructed plots in Figure 1 are almost ideal annual phenological curves. The reconstructions are smooth and captures the essential part of intra-annual variability in the NDVI. The reconstruction in Figure 1.a, which is representative of the northern boreal/deciduous phenology has the characteristic bell-shaped/sigmoidal curve with an interpolated peak NDVI activity between the 6 th and 7 th months. The reconstructed curves for the desert (Figure 1.b) and tropical areas (Figure 1.c) behave on the ideal sense, in that the curve represents phenology which has very little change, or if they do change, the increments are incurred at rather small values or that which are gradual through time. The reconstructed curve in Figure 1.b could be observed to be decreasing gradually through time, as expected for some desert areas which may harbor to some extent, some form of vegetation (considering that the resolution of the pixel under study is around 8 kilometers, considerable integration of vegetated and non-vegetated areas may have been inevitable). The curve in this case, could be observed to decrease in NDVI value coincidental with northern hemisphere seasonal variation, and reaches its lowest NDVI value around northern winter. This trend could be explained by the geographical location of the test/sampled pixels for the desert dataset. The test pixels are located in the northern hemisphere.

An opposite, slightly increasing trend towards the end of the year (or what is northern hemisphere winter), could however be observed with the reconstructed curve of the tropical dataset. Again this could well be explained by the geographical location of the sampled pixels.

For the tropical dataset, pixels are located in the southern hemisphere (central Brazil). Whereas the northern hemisphere experiences winter at this time of the year, the reverse is true for the southern counterpart, in this case, summer is being experienced, and so the slightly increasing trend in the curve of the tropical dataset.

The reconstructed curve for the two-time crop, Figure 1.d (in this case, the cropping/phenology pattern of rice) is remarkable. The two peaks which represent crop (rice) maturity and valleys, which represent harvesting and initial cultivation (or sowing) have been clearly reconstructed.

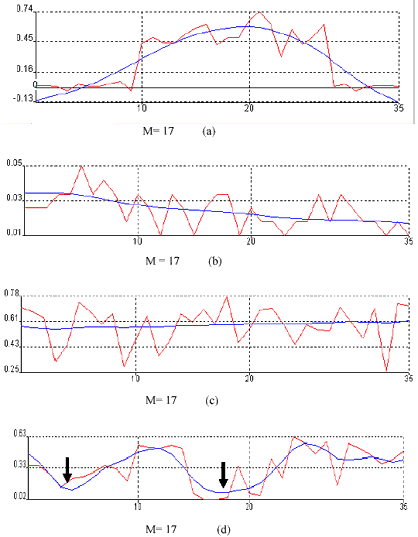
Figure 1. Original (in red) and reconstructed series (in blue) of 1-year (1984) NDVI profiles of different landcover types, with lag (M) = 17 (a) boreal- PC1 and 2; (b) desert-PC1; (c) tropical-PC1; (d) two-time crop-PC1, 2, and 3. Note the significant valley detected in (d) for the two-time crop (arrows indicating “valleys” representative of harvesting/sowing seasons).
3. CONCLUSION
In spite of relatively small length of this sequence, SSA is able to reveal the components corresponding to the main signal and separate it from noise, as well as efficiently reconstruct the original time series.

This study has shown that the SSA may be used as an alternative method for removing both low and high value noise in NDVI profile data. SSA made over extensive periods are effective in reducing influences due to cloud contamination and variable viewing conditions, but much like the previous profile extraction methods, the length of the lag window may affect the inclusion or exclusion of noise in the reconstructed series. The value of the lag window, M < [N/2+1] substantially provides a good fitting of the NDVI profile.

The phenomenon of surface anisotropy due to specific viewing angles and atmospheric conditions can elicit high NDVI values generally in the forward scattering direction (Gutman, 1991). All previous methods, like the BISE, MVC, and MVI will always include and retain spurious high values from data transmission errors and anistropic effects. Whereas, other previous algorithms introduce a bias due to the assumption that a lower values of NDVI are considered only as noise while retaining higher values, the SSA does not suffer from such a bias, since the whole process is data-adaptive and assumes no specific model of the process being analyzed (Vautard and Ghil, 1989).

On the whole, the SSA is a sufficiently advantageous and promising method for the reconstruction and prediction of NDVI phenology.

4. REFERENCES:

Agbu, P.A., and James, M.E. (1994). The NOAA/NASA Pathfinder AVHRR Land Data Set Users’ Manual. Goddard Distributed Archive Center, NASA, Goddard Space Flight Center, Greenbelt.
Allen, M.R. and Smith, L.A. (1997). Optimal filtering in singular spectrum analysis. Physics Lett., 234, 419-428.
Allen, M.R. and Smith, L.A. (1996). Monte Carlo SSA: detecting irregular oscillations in the presence of coloured noise. J. of Climate, 9, 3373-3404.
Ariño, O., Dedieu, G., and Deschamps, P.Y. (1991). Determination of satellite land surface reflectances using METEOSAT and NOAA/AVHRR shortwave channel data. Int. J. Remote Sens.,, 13, 12, 2263-2287.
Bartholome’, E. (1991). Remote sensing and agricultural production monitoring in the Sahelian countries. In Remote Sensing and Geographical Information Systems for Resource Management in Developing Countries, edited by A.S. Belwrad and C.R.Valenzuela (Dordrecht: Kluwer Academic), pp. 189-214.
Broomhead, D.S. and King, G.P. (1986a). Extracting qualitative dynamics from experimental data. Physica D., 20, 217-236.
Broomhead, D.S. and King, G.P. (1986b). On the qualitative analysis of experimental dynamic systems. In: Nonlinear Phenomena and Chaos. Ed. S. Sarkar. (Adam Hilger, Bristol). Pp. 113- 144.
Cao, L., Hong, Y., Fang, H. and He, G. (1995). Predicting chaotic time series with wavelet networks. Phyisica D., 85, 225-238.
Casdagli, M. (1989). Nonlinear prediction of chaotic time series. Physica D., 35, 335-356. Danilov, D.L. and Zhiglyavsky, A. .A. (1997). Principal components of time series: the caterpillar method. (Saint Petersburg Univ. Press).