Multi-temporal Cloud Removing Technique via Adaptive Kalman Filter

Multi-temporal Cloud Removing Technique via Adaptive Kalman Filter

Kobchai DEJHAN, Sompong WISETPHANICHKIJ and Chaiwut ARIYAPATTANAKUL
Faculty of Engineering and Research Center for Communications and Information Technology
King Mongkut’s Institute of Technology Ladkrabang, Bangkok 10520, Thailand
Tel: +66-2-3264238, +66-2-326-4242, Fax: +66-2-326-4554
e-mail: {sompong, kobchai}@telecom.kmitl.ac.th Email: sompong@telecom.kmitl.ac.th, kobchai@telecom.kmitl.ac.th

Chanchai Pienvijarnpong
Geo-Informatiocs and Space Technology Developemnt Agency (GISTDA)
Chalongkrug Road, Ladkrabang, Bangkok 10520, Thailand e-mail: chanchai@gistda.or.th
Email: chanchai@gistda.or.th

ABSTRACT
This paper proposes cloud removing technique by adaptive Kalman filter. The multi-temporal images, cloud-cover image and reference image are applied to the filter. This recursive nature of filter is one of the very appealing features which is designed to operate on all of the data directly for each estimate and instead recursively conditions the current estimate on all of the past measurement. The output of filters with 3 different raster scans then combined together to achieve the cloud removed result.

1. INTRODUCTION
The image distortion due to cloud cover and cloud shadow is a classical problem of visible band of remote sensing imagery. Especially, for non-stationary satellite that commonly found in earth resource observation application. The long recurrent period that can up to 44 days for JERS-1, 26 days for SPOT or 16 days for LANDSAT turn to be a trouble for monitoring (change detection) problem when the continuity of acquired scene was broken by cloud cover problem. To recovery the hidden area under cloud and its shadow, the various techniques were proposed in the previous papers. The histogram-based technique is a classical method that can be found in previous paper [1]. The fusion techniques [2] are also adopted for this task [3]. The key of these techniques is to find out the hidden area on corrupted image and then replace with clearer or reference image. The effectiveness of these methods depends on how to extract the cloud over or hidden area efficiently. This paper proposes the alternative way to solve this problem by reconstruct the distort area. By feeding these two images, cloud-covered image and reference image to the well known recursive adaptive filter, the discrete Kalman’s filter [4]. The recovering of hidden area can be accomplished within 5 steps for each pixel,

The Kalman filter estimates a process by using a form of feedback control. It estimates the process state at some time and then obtains the feedback in the form of (noisy) measurements. As such, the equations for the Kalman filter fall into groups, time update equations and measurement update equations. The time update equations are responsible for projecting forward (in time) the current state and error covariance estimates to obtain the a priori estimates for the next time step. The measurement update equations are responsible for the feedback i.e., for incorporating a new measurement into the a priori estimate to obtain an improved posteriori estimate. The time update equations can also be thought of as predictor equations, while the measurement update equations can be thought of as corrector equations. The estimated output of the filters then combined to achieve the cloud removing. All details of proposed scheme are mentioned in section 2. The subsequence section shows some samples of cloud removing result by proposed scheme.

2. CLOUD REMOVING SCHEME
Firstly, the two images, the cloud-covered and reference image, are registered and cropped precisely to bound the corresponding area. Due to the 1-D adaptive Kalman filter (order 32) is used in this paper. Therefore, three fashions of zigzag raster scans have to perform before applying to the filter as shown in fig.1. Let the scanned clouded image to be a corrupted measurement input signal and setting the scanned reference image to be a predicted state, the reconstructed image can be got by the estimated output of adaptive Kalman filter. Finally, three output filters are averaged to reduce the uncertainty in each raster scans.

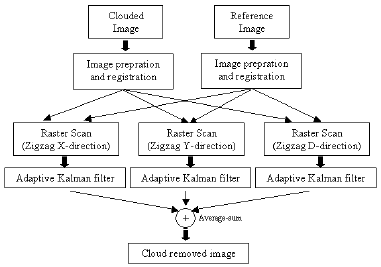
Fig.1 The proposed scheme
3. RESULTS
To verify the proposed scheme, the LANDSAT-5 TM images on path 129 row 51 at the middle part of Thailand that shown in fig.2 are used. The reference image is acquired on March 26, 2004 that clear from cloud (fig.3a) and the cloud-covered image is acquired on May 29, 2004 (fig.3b). Table 1. shows the estimated output and corresponding error. Finally, three outputs are averaged to obtain the cloud removed result.

Fig.2 LANSAT-5 orbital path around Thailand Study area

Fig. 3 LANDSAT5 (path 129, row 51)

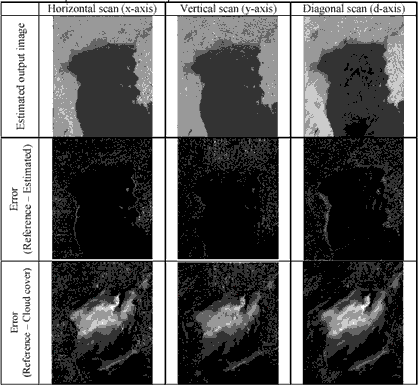
Table 1. Adaptive Kalman filter output

Fig.4 Cloud removing result
4. CONCLUSION
The proposed scheme successfully proofs the cloud removing efficiency. However, it highly depends on the perfect registration between these two images. This drive the adaptive Kalman filter well estimates the hidden area. Furthermore, the reconstructed results also depend on the cloud cover area. If the measurement (cloud cover image) is very uncertain compare with reference image, then the filtered residual is resulted mainly by the noise. Kalman filter then self adjusts by updating its gain proportional to measurement signal. On the other hand, if the uncertainty in the measurement is small and that in the state estimate is big, then the filtered residual contains considerable information about errors in the state estimate and strong correction should be made to the state estimate. This results the small filter gain and estimate output now will follow the reference image.

5. REFERENCE

F. Cheevasuvit, K. Dejhan and T. Tanapapanich, “Cloud cover and cloud shadow removing based on 2-dimensional histogram,” ACRS1992, Oct. 1992.
J. Nunez, X. Otazu and R. Ardiol, “Multiresolution-Based Image Fusion with Additive Wavelet Decomposistion,” IEEE Tran, Geoscience and Remote Sensing, vol.37, No.3, pp. 1203-1211, May 1999.
S. Wisetphanichkij, K. Dejhan and F. Cheevasuvit, “Multi-temporal Cloud Removing Based on Image Fusion with Additive Wavelet decomposition”, ACRS1999, Oct. 1999.
M. H. Hayes, Statisitcal Digital Signal Processing and Modeling, John Wiley & Sons Inc., USA, 1996.
R. C. Conzalezand and R.E. Woods, Digital Image Processing, Addition-Wesley Publishing Company, USA, Sep. 1993.