| GISdevelopment.net ---> AARS ---> ACRS 2004 ---> Data Processing: High Resolution Data Processing |
A Modified Watershed
Technique for Segmentation of High Resolution Satellite Images
Li-Yu Chang and Chi-Farn
Chen
Center for Space and Remote Sensing Research
National Central University
No.300, Jungda Rd, Jhongli City, Taoyuan, 320, TAIWAN
Tel: 886-3-4227151-57688, Fax: 886-3-4264301
E-mail: lychang@csrsr.ncu.edu.tw
Center for Space and Remote Sensing Research
National Central University
No.300, Jungda Rd, Jhongli City, Taoyuan, 320, TAIWAN
Tel: 886-3-4227151-57688, Fax: 886-3-4264301
E-mail: lychang@csrsr.ncu.edu.tw
ABSTRACT
Watershed segmentation is a widely used technique for image partitioning. However, over-segmentation normally occurs when the smoothing process is not operated properly. For example, improper selection of smoothing scheme and parameters will not only wipe out the detail of image content but also affect the accuracy of following feature extraction. In order to overcome these drawbacks, a modified watershed segmentation method based on the edge intensity filtering is proposed. An experiment using both QuickBird multi-spectral and panchromatic images is performed to test the proposed scheme. The result shows that the proposed scheme can generate reasonable and simplified segmentation output for different type of objects.
1. INTRODUCTION
Due to the recent progress of satellite imaging system, the image resolution of some commercial satellites can reach to less than 1 meter in panchromatic mode. Such high spatial resolution images certainly will provide lots of detail for remote sensing users. Nevertheless, the complex image content will make it difficult to develop image algorithms for automated image feature extraction and pattern recognition. Image segmentation is one of the useful techniques to extract regions from satellite images. It is usually regarded as a preprocessing procedure for image classification (Black, 1998). Among numerous segmentation techniques, watershed algorithm is a sophisticated technique for extracting region features from images (Hagyard, 1996 and Perona, 1990). The basic concept of watershed algorithm is to perform watershed operation on an edge image that is obtained from the source data. However, the complex texture of images usually causes over-segmentation. To avoid such consequence, a smoothing filter must be used in advance (Scheunders, 2001). Nevertheless, improper selection of smoothing filter or its parameters will not only smear the detail of source data but also affect the edge accuracy of the extracted feature. Therefore, the role of smoothing filter becomes a key factor in the whole processing procedures. There are some smoothing algorithms which can reduce noise and preserve accurate edge information simultaneously (Thomas, 1987 and Vincent, 1997). However, these algorithms still need user to select a suitable windows size. Besides, the relation between the scale of segmented object and the windows size of smoothing filter is highly dependent and nontrivial.
A modified watershed segmentation algorithm is proposed to improve this weakness. Unlike the traditional approach, we directly apply watershed segmentation to the edge image of input data without smoothing, which apparently will cause over-segmentation. However, the most detail of segment information is preserved. Then, an iterative patch merging procedure is applied to this result to create multiple segmentation layers. At last, an edge intensity filtering technique is applied to the multiple segmentation layers to generate final result.
2. METHODOLOGY
In this study, QuickBird multi-spectral and panchromatic images are considered as input dataset. For extracting the most detail information from this dataset, the multi-spectral and panchromatic modes of images are fused together for segmentation. The algorithm used here for images fusion is based on the Brovey transformation method (Roller, 1980 and Hallada, 1983). In fact, Brovey transformation only multiplies normalized multi-spectral image and original panchromatic image to generate fusion result. Although Brovey transformation may produce spectral distortion in the result (Hill, 1999), this method in deed can preserve the most original information of input data without any nonlinear modification. However, for keeping the mean of fused image the same as original multi-spectral image, a modified Brovey transformation method is used. The modified algorithm is as follows:
F(n) = M(n) x P / P mean n = 1..4 (1)
Where
P is the panchromatic image.
M(n) is the n-th band of multi-spectral image.
F(n) is the n-th band of fused image.
P mean is the mean value of panchromatic image.
The following is the segmentation procedure for fused image. Firstly, we apply Sobel operators to input images in column and row directions to create two edge images of fused image. Secondly, the square root of the sum of squares taken from the two edge images in previous step is used to measure edge intensity of source data. Thirdly, based on the watershed technique of morphological theory, the concave regions in the image of edge intensity can be detected and result an initial segmentation. Fourthly, an iterative patch merging procedure by various threshold of mean difference is applied to the result of watershed to create multiple segmentation layers. In addition, for each segmentation layer, another iterative processing is needed for merging neighboring patches to ensure that the all mean differences between neighboring patches are greater than a certain threshold.
Therefore, after the processing of iterative patch merging procedure, the spectral variation of patches in each segmentation layer is different. The spectral variation of patches becomes coarser as the region mean difference increase in each layer. This implies that the intensity of the patch edges should be larger in coarser layer. Hence, the intensity of the patch edges can be easily calculated by counting edge numbers for each pixel across all bands and all layers.
The last step is a filtering procedure over the intensity of the patch edges. There are two criterions should be satisfied for a valid edge. First, the intensity of any point along an edge should be equal to the maximum intensity in a local window with certain size. Second, the intensity of any point along an edge should be larger than the mean of intensity of all patch edges. The two criterions are used for local and global filtering respectively. Figure 1 is the flow chart of proposed scheme.
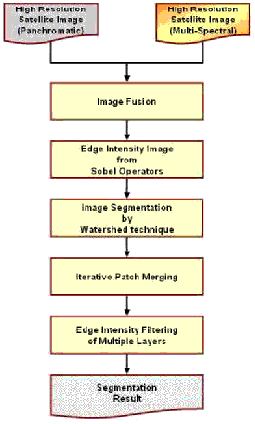
Figure 1. The flow chart of proposed scheme.
3. EXPERIMENTAL RESULT
Figure 2 Shows both QuickBird multi-spectral and panchromatic images used in this study. The ground coverage of this dataset is 360m by 360m. Figure 3 illustrates the fused image of the two spectral modes. After applying watershed operation without smoothing, an over-segmentation is observed (Figure 4). Figure 5 indicates the results during iterative patch merging procedure by different threshold of mean difference. The thresholds of mean difference are 15 and 45 respectively. Figure 6 shows the intensity of the patch edges calculated by counting edge numbers for each pixel across all bands and all layers. After applying the filtering procedure over the intensity of the patch edges, the final result is generated. Notice that the window size is 11 pixels by 11 pixels in the local filtering. Figure 7 is the result of proposed scheme overlay on the fused image.

Figure 2. The QuickBird dataset acquired on Oct. 17, 2002 used in this study.
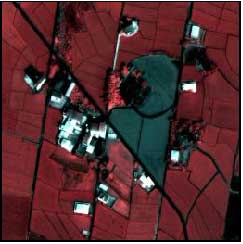
Figure 3. The fused image of the two spectral modes.
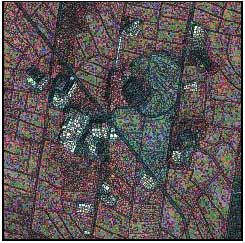
Figure 4. Over-segmentation caused by watershed operation without smoothing.
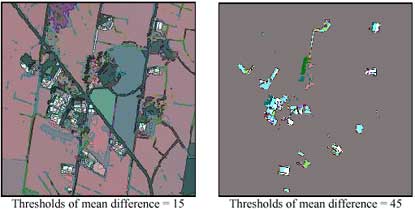
Figure 5. The results during iterative patch merging procedure.

Figure 6. The intensity of the patch edges calculated for each pixel.

Figure 7. The result of proposed scheme overlay on the fused image.
4. CONCLUSION
In this study, a modified watershed segmentation method based on the edge intensity filtering of multiple layers is proposed to improve the conventional approach. Using both local and global edge intensity filtering can select relatively useful edges over image areas with different variations. The experimental result shows that the most important boundaries are successfully detected. This result may provide suitable information for image classification and object identification in future researches.
REFERENCES
- Black, M., G. Sapiro, D. Marimont, and D. Heeger, 1998. Robust anisotropic diffusion. IEEE Transactions on image processing, 7(3), pp. 421431.
- Hagyard, D., M. Razaz, and P. Atkin, 1996. Analysis of watershed algorithms for greyscale images. Proceedings of the IEEE International Conference on Image Processing, 3, pp. 4144.
- Hallada, W.A. and S. Cox, 1983. Image sharpening for mixed spatial and spectral resolution satellite systems. Proceeding of the 17th International Symposium on Remote Sensing of Environment, pp. 10231032.
- Hill, J., C. Diemer, O. Stφver and Th. Udelhoven, 1999. A local correlation approach for the fusion of remote sensing data with different spatial resolutions in forestry applications. International Archives of Photogrammetry and Remote Sensing, 32, part 7-4-3, W6
- Perona, P. and J. Malik, 1990. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(7), pp. 629639.
- Roller, N.E.G. and S. Cox, 1980. Comparison of Landsat MSS and merged MSS/RBV data for analysis of natural vegetation. Proceeding of the 14th International Symposium on Remote Sensing of Environment, pp. 10011007.
- Scheunders, P., 2001. Multivalued image segmentation based on first fundamental form. Proceeding of International Conference on Image Analysis and Processing, pp. 185190.
- Thomas, I. L., V.M. Benning, and N.P. Ching, 1987. Classification of remotely sensed images. Adam Hilger, Bristol.
- Vincent, L. and P. Soille, 1991. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13, pp. 583593.