Automated Procedure of a Prototype Mapping System

Acquisition method of high accuracy ground control points for high - resolution satellite imagery

Takeshi MIYATA and Masataka TAKAGI
Kochi University of Technology
Tosayamada-cho, Kochi, 782-8502, Japan
Email: 085517e@gs.kochi-tech.ac.jp

ABSTRACT
Currently, high-resolution satellite imageries as less than 1m resolutions are used in many fields. For example, land use mapping, urban planning, disaster monitoring, and so on. They are expected to be overlaid with other GIS data and updating existing maps. Therefore, high accurate geometric correction is necessary to analyze high-resolution data. However, it is difficult to acquire highly accurate ground control points (GCP) and the corresponded image control points (ICP). Because, acquisition of the high accuracy ICP by using visual interpretation is very difficult. In this study, acquisition method of high accuracy GCP and the corresponded ICP was discussed.

Field surveying by kinematic using GPS was used for generating polygon data for GCP. And center of gravity of the polygon was used as GCP. Error of coordinates in GCP dataset by field surveying can be decrease by calculating center of gravity of the polygon. Calculation results showed less than 0.1 m error. It was enough accuracy as GCP.

An efficiency of center of gravity calculation for high accurate ICP were evaluated by generating simulation images from GCP polygons. The simulations were carried out under some conditions as follows ;

Shape of GCP polygon. – Elevation difference in GCP Polygon.
Off-nadir angle of satellite image. – Error in classification.

The simulated images were generated from GCP polygons by transformation using collinearity equation. Center of gravity as ICP were also calculated the simulated polygon image. The results showed shape of polygon and off-nadir angle influence to accuracy of ICP. Required accuracy were satisfied under the condition that “off-nadir angle” ranges from 0°to 10°and “flat area”.

1. INTRODUCTION
High-resolution satellite image are expected to be overlaid with other GIS data and updating existing map. Therefore, highly accurate geometric correction is necessary to rectify high-resolution data. In photogrammetry, many metric targets were used for geometric correction. However, the targets are so small that it is not taken in high-resolution satellite image. Therefore, acquiring high accuracy GCP and the corresponded ICP is difficult. Especially, acquisition of the high accuracy ICP by using visual interpretation is very difficult.

2. OBJECTIVES
In this study, acquisition method of high accuracy GCP and the corresponded ICP by using “Polygon data” was established. A center of gravity of the polygon data will be used as high accurate GCP and ICP. GCP was acquired from polygon data by kinematic survey using GPS. ICP was acquired by simulated image classification from the corresponded GCP polygons. Required accuracy of GCP was less than 0.1m error. And required accuracy of ICP was less than 1/10 pixel error.

3. CALCULATION METHOD OF CENTER OF GRAVITY FROM POLYGON DATA

3.1 In Case of GCP Polygon
GCP polygon data were generated by kinematic survey using GPS. A center of gravity was calculated by triangurated area and the center of gravity. Figure3.1 showed calculation flow of a center of gravity. Figure3.2 showed example of surveying points and calculated triangle for acquisition of GCP. Equations for the calculation showed as fllows;

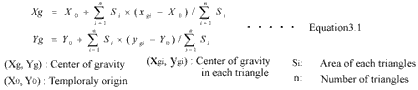
The calculated center of gravity of a polygon were used as GCP. Then, error of GCP by field surveying will be decrease by calculating center of gravity of the polygon.

3.2 In Case of ICP
ICP polygon image were extracted from the high-resolution satellite image. ICP polygon image was binarized for calculating a center of gravity. A center of gravity was calculated average of all pixels coordinate included GCP polygon by using following eqations. The calculated a center of gravity of a polygon were used as ICP. Figure3.3 expressed example of corresponded image for acquisition of ICP.

Figure3.1 Flow chart -Calculation method of a center of gravity

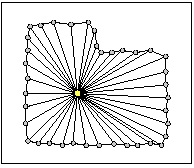
Figure3.2 Example GCP polygon

Figure3.3 ICP polygon image
4. PROPOSED METHOD TO ACQUIRE GCP
GCP polygon was acquired by kinematic survey using GPS. Because, kinematic survey did not take much time and it was easily acquired polygon data. Figure4.1 showed test area for verification of GCP accuracy. Figure4.2 showed generated verification GCP polygon data by Total Station surveying (0.5m interval). Accuracy of Total Station was ±5mm error. It was enough to verify GCP accuracy. Figure4.3 showed acquired polygon data by using kinematic survey. Calculation of a center of gravity for two polygons data were carried out for comparison. Table4.1 showed verification result. Required accuracy showed satisfied required accuracy 0.1m error. It was enough accuracy as GCP.

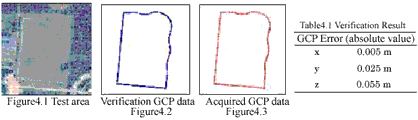
Figure4.1 Test area Verification GCP data Acquired GCP data Figure4.2 Figure4.3
5. PROPOSED METHOD TO ACQUIRE ICP

5.1 Simulation Image Generation
It was difficult to verify ICP. So, an efficiency of center of gravity calculation for high accuracy ICP were evaluated by simulation. The simulation was carried out under some conditions as follows;

– Shape of GCP polygon. – Elevation difference in GCP Polygon.
– Off-nadir angle of satellite image. – Error in classification.

The simulated image were generated from GCP polygon data by transformation using collinearity equation. Center of gravity as ICP were also calculated the simulated polygon image.

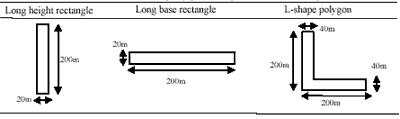
Table 5.1 Condition of polygon shape for simulating GCP

Table5.2 Elevation difference in GCP Polygon

5.1.1 Shape of GCP Polygon
In this study, three land shapes were generated. Table5.1 showed polygon shape and size for simulation. Table5.2 showed Elevation difference in GCP Polygon for simulation.

5.1.2 Off-Nadir Angle of Satellite Imagery
Figure5.1 showed Off-nadir angle of satellite image for simulation. Conditions of satellite was referred IKONOS satellite image. Table5.3 showed parameters of simulated platform.

Table5.3 Parameters of platform

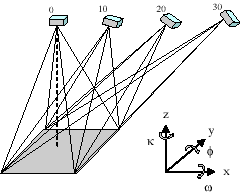
Figure 5.1 Condition of Off-nadir angle for simulation
5.1.3 Error Condition in Classification
Figure5.2 showed error condition in classification. In generated polygon images random error were added. The random error was set ±0.5pixel. Because, when the corresponded polygon as ICP were extracted from the high-resolution satellite image, the error will occurred in image classification.

Figure 5.2 Error condition of classification
5.2 Verification Flow of Simulated ICP

(Xi, Yi, Zi) under the some conditions. And a center of gravity was calculated from polygon data for GCP (Xg,Yg,Zg). Next, generated polygon data were transformed into image coordinate by using collinearity equation. Classification error added to transformed coordinate (U’i, V’i). A center of gravity was calculated from transformed coordinate (U’g, V’g). Finally, (U’g, V’g) were compared with (Ug, Vg) which calculate directly from GCP polygon.

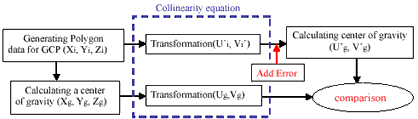
Figure5.3 showed Verification Flow of ICP. Firstly, polygon data was generated from GCP
5.3 Verification Results of Simulated ICP
Simulation results showed figure5.4. In case of long height rectangle polygon, error of “v” direction has tendency to increase with off-nadir angle. In case of long base rectangle polygon, required accuracy was almost satisfied in all conditions. In case of L-shape polygon, error showed less than 0.2 pixel in all conditions.

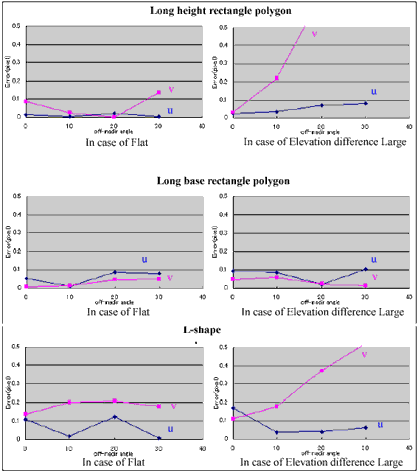
Figure5.4 Relationship between off-nadir and Error in each condition of
6. CONCLUSIONS
In this study, GCP polygon was acquired by kinematic survey using GPS. And GCP polygon data were carried out comparison by verification data. Required accuracy of GCP showed less than 0.1 m. Required accuracy was satisfied.

An efficiency of center of gravity calculation for high accuracy ICP were evaluated by the simulation. The simulation results were depended on shape of polygon, off-nadir angle and elevation difference. Required accuracy was satisfied all shape of ICP polygons under the condition that “off-nadir angle ” ranges from 0°to 10°and “flat area”. However, elevation difference made unstable results.

As further study, several polygons for GCP by kinematic survey using GPS will be acquired. And Geometric correction must be performed using GCP polygons and ICP polygons.

7. REFERENCES

Takae KADOTA and Masataka TAKAGI, “Acquisition Method of Ground Control Points for High Resolution Satellite Imagery” Lecture papers of the 25 th Asian Conference on Remote Sensing, 2002
Takae KADOTA, Eriko NAKAGOE and Masataka TAKAGI, “Geometric Correction of IKONOS Imagery by 3D Affine Transform” Proceeding of Japan Society of Photogrammetry and Remote sensing (in Japanese), 2002