GISdevelopment.net ---> AARS ---> ACRS 2004 ---> Data Processing: High Resolution Data Processing An Improved Compression Algorithm for SAR Images Using Wavelet Transform Sang Huiyong¹, Lin Hui¹, Guo Huadong², and Li Xiang¹ ¹ The department of Geography and Resource Management, The Chinese University of Hong Kong, Shatin, NT, Hong Kong, Email: sanghuiyong@cuhk.edu.hk, huilin@cuhk.edu.hk ² The Institute of Remote Sensing Applications, Chinese Academy of Sciences Email: 085517e@gs.kochi-tech.ac.jp Abstract Several characteristics of SAR (Synthetic Aperture Radar) images will influence the design of image compression algorithms. The first is speckles in SAR images which are stochastic and out-of-order and severely damage SAR images’ quality. Secondly, there is not only detailed texture information but also a lot of homogeneous regions, which make it necessary to decrease encoding bits of homogeneous regions. Thirdly, SAR image data have higher dynamic range than that of optical images, and this difference means that the encoding/decoding algorithms designed for optical images are not optimal for SAR data and even not appropriate at all. In this work, we improved SPECK (Set Partitioning Embedded Block) algorithm based on SAR images characteristics. Our algorithm is more effective in Mean Square Error(MSE), Peak Signal to Quantization Noise Ratio(PSQNR), Average Signal to Quantization Noise Ratio(ASQNR) and visual aspect, compared with the results of conventional SPIHT algorithm, when applied for Chinese airborne L-SAR images. 1. Introduction Synthetic aperture radar (SAR) is a kind of remote sensing technology which synthesizes far bigger aperture than real aperture radar through utilization the motion of radar transmitting devices and can generate radar images with higher resolution. Radar system produces a mass of data for objects imaging and terrain mapping. However, with the rapidly increasing data collection capacity, its ability to transmit and store data is relatively weaker. Moreover, although the storage density is gradually enhanced along with the development of sciences and technologies, the ability of generating new data is increasing more quickly. Many measures can reduce data rate while depressing the whole running effect of the system. For instance, reducing pulse repeating frequency would introduce blurred azimuth and reduced azimuth resolution unless the system use longer azimuth antenna. Also, reducing range resolution would depress system bandwidth. Only to simply reduce quantified bits would increase digitized noise, and as a result damage the pulse response function, image dynamic range and radiation accuracy. Therefore, in order to improve SAR system, data compression algorithms with high efficiency have become an important tool. Thus it needs to develop data encoding/decoding algorithms and at the same time gain high compression ratio, on condition that maintaining acceptable image quality. Since wavelet transform has been introduced as a signal processing tool, its applications, especially discrete wavelet transform (DWT) becomes more and more common in the field of image compression. It is because its multi-resolution and multi-decomposition characteristics can be used in high efficient image analysis that wavelet transform wins much recognition, and its popular applications include SAR image analysis, speckle filtering, data compression and image multi-spectral analysis. Several characteristics of SAR images will influence the design of image compression algorithms (Zeng, 2001), such as speckles and high dynamic range. These differences between SAR images and optical remote sensing images mean that the encoding/decoding algorithms for optical images are not optimal for SAR data and even not appropriate at all. Wavelet transforms, especially discrete wavelet transform (DWT), have received significant attention due to their multiresolution decomposition (Pearlman, et al), which make them efficient in image analysis. Using DWT, terrain segmentation, speckle noise filtering and image compression can be completed in a single decomposition-reconstruction process (Zeng, 2001). In this work, we introduced Set Partitioning Embedded Block (SPECK) encoding scheme based on SAR images characteristics. Our results are compared with the conventional set partitioning in hierarchical trees (SPIHT) algorithm (Said A. and Pearlman W. A., 1996), which also utilized embedded hierarchical tree and progressive transmission based on wavelet transform theory, and show that our proposed method is more effective for SAR image compression and visual interpretation. 2. The modification to SPECK coder for SAR images Said and Pearlman (Said A. and Pearlman W. A., 1996) introduced set partitioning and significance testing on hierarchical structures of transformed images in their SPIHT (Set Partitioning In Hierarchical Trees) algorithm, which successfully extended and improved Shapiro’s EZW (Embedded Zerotree Wavelet) algorithm (Shapiro, 1993). In SPIHT and EZW algorithms, insignificant coefficients are mainly mapped in a tree structure. Although these two algorithms used the relativity between insignificant coefficients in different subbands, they did not completely exploit the relativity between insignificant coefficients in the same subband. So Pearlman and others proposed a Set Partitioning Embedded block (SPECK) scheme (Pearlman, et al), which is a comparatively efficient algorithm in embedded hierarchical image encoding schemes. A more detailed description about SPECK coder can be referred to http://www.cipr.rpi.edu/~pearlman/papers/csvt02_pins.pdf. Here, we just present our modification to SPECK coder according to SAR image characteristics as follows: (1) One merit of wavelet transform is that speckles filtering, image compression and other processes can be completed in the wavelet transform field. Because most speckles in SAR images are multiplicative noise and the dynamic range of SAR data is large, only wavelet transform will increase the complexity in quantification process, and simultaneously increase coding bits and decrease compression ratio. Thus, we will carry through the logarithm transform to make multiplicative noise become additive noise before wavelet transform. (2) There are many speckles in SAR images, so speckles filtering is done before image compression. Speckles filtering method adopted the adaptive wavelet-based threshold denoising algorithm using image gradient (Sang, 2004) , which can effectively reduce speckle in uniform areas and preserve edge and texture information in heterogeneous regions. Noise coefficients are generally within the subbands with higher frequency, so the lowest subband does not need speckle filtering, which can increase running speed (Sang, 2004). (3) The lowest subband contains most energy of the raw image, and the absolute values of the coefficients in the lowest subband are far larger than those in other subbands. Thus, it needs to increase the quantified coefficients step by step in order to recover the image quality, and otherwise comparatively little loss in the lowest subband would influence the recovery of image quality severely. Thereby, the lowest subband is separated from other subbands and encoded with its own threshold, and also the relatively small compression ratio will gain less distortion. The lowest subband carries most texture information and speckles are most included in higher frequency subbands. Thus the lowest subband is processed apart from other subbands due to its far larger coefficients values, so the threshold is for all sunbands except for the lowest subband, which is different from that in the lowest subband. In this way, it will be avoided that scanning repeat times are increased and coding precision in higher subbands is decreased owing to far bigger coefficient values in the lowest subband. (4) The scanning repetition in SPECK algorithm is from the initial set S, which in fact is the lowest subband (LL4 in 4-wavelet transform). The initiated S is HL4 in our algorithm, and the scanning order of the whole image is from low subbands to high subbands, that is HL4, LH4, HH4, Hl3, Lh3, HH3, … , LH1, HH1. In this way, it does not require the process of octave partition as in SPECK algorithm, running time is saved, scanning times are reduced, and storage space is decreased. Because the set I includes the remaining subbands except the lowest subband, the required storage space in the process of octave partition for the set I in SPECK algorithm is far more than that in the process of only scanning one single subband (e.g. HH3) in our algorithm. Because the energy in wavelet frequency field is decreased from low frequency to high frequency, the scanning repetition can be stopped at will according to the requirement, which is consistent with the idea in SPECK algorithm. Like in SPECK algorithm, the current subband or the current set S is scanned and checked with the threshold at one side, and processed with octave partition for threshold checking next time at another side. 3. Results and discussion The Institute of Electronics, Chinese Academy of Sciences, carried out an airborne L-SAR flight in the north of Beijing for the layout of 2008 Beijing Olympics, which was also one project of the Information Acquisition & Processing Program, Ministry of Science and Technology of China. The proposed method was tested with the 256*256 L-SAR image from this project. The filters used in wavelet decomposition are 9/7 tap biorthogonal filters (Daubechies, 1988). A periodical extension was used at the image edges to settle the marginal distortion (Quegan, 1990). One of the merits of the proposed embedded coder is that the bit rate can be obtained accurately, other than estimated based on information entropy, and the distortion can be gotten exactly from the restored image due to progressive transmission. In order to evaluate the effectiveness of our SAR image compression algorithm, several quantitative and qualitative evaluation indices are used in our algorithm and in SPIHT algorithm respectively. 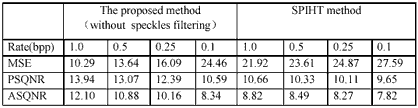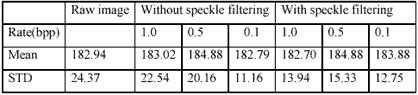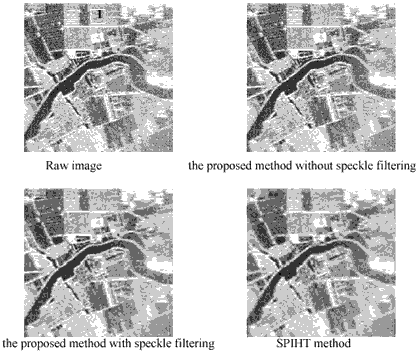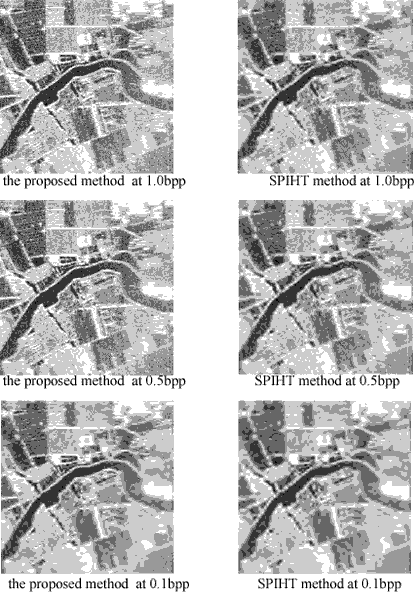Table1 compression performance of the proposed method and SPIHT algorithm Table 2 Mean and Standard deviation calculated for region I for the proposed method with and without speckle filtering Figure 1 comparison for the compression/filtering results at 1.0bpp Figure 2 comparison for the compression results at different rates (1) Mean Square Error (MSE): defined as are values of the pixel (i, j) in the raw image and the restored image respectively, and N is the number of pixels. MSE is the absolute encoding error between the raw image and the restored image. (2) Peak Signal to Quantization Noise Ratio (PSQNR): defined as the ratio of the peak signal and MSE. (3) Average Signal to Quantization Noise Ratio (ASQNR): defined as the ratio of the average signal and MSE. (4) Visual effect. Our results are compared with SPIHT encoding method with the above quantitative and qualitative standards. Figure 1 shows the raw image, and the result coded with the proposed method, the result coded with the proposed method after filtering process and, the result coded with SPIHT algorithm, at the rate 1.0bpp. Figure 2 shows the results coded at the rates 0.1, 0.5 and 1.0 bpp using the proposed coder and SPIHT coder respectively. The quantitative evaluation results of the coded images at different rates using the former two coders are listed in Table1, and Table2 shows the Mean Value and Standard Deviation at the region I, highlight in raw image in figure 1, which is a 32×32 homogeneous region, when the image was filtered speckles or not before coded at rates 1.0, 0.5 and 0.1 bpp with the proposed encoding scheme. The proposed algorithm is more effective in SAR images, especially at high compression ratio, not only from the former quantitative evaluation standards MSE, PSQNR and ASQNR, but also from the visual effects. There are less speckles in filtered images than not filtered images no matter coded at what rate in table2 and figure 1. However, the fault is that the former lost more detailed information compared with the latter. Even if the filtering process tries to keep edge information, the flatting effect still exists to some extent, which makes images more homogeneous. In table I, except that the results coded with the proposed method are better than with SPIHT method for SAR images at different rates, with the increase of the bit rate, MSE gradually reduced, and PSQNR and ASQNR are gradually increased, which validates that the images coded at high rates are more like the raw image than the images coded at low rates and the distortion is lower. From the results showed in figure2, texture information is lost much in the images coded at high compression ratio, namely low coding rate, which will not benefit image interpretation. Thus in general, high compression ratio is not appropriate for SAR images. 4. Conclusion Because SAR images have different characteristics from optical remote sensing images, common compression algorithms applying for optical images are not completely appropriate for SAR images. The proposed compression method is an improvement of SPECK coder according to SAR images. MSE, PSQNR, ASQNR and visual effect were used to evaluate the proposed method. The results show that the proposed method is more effective for SAR images than conventional SPIHT algorithm, and has better visual effects and is useful for image calibration and visual interpretation. References Shapiro, J. M.(1993) Embedded image coding using zerotree of wavelet coefficients, IEEE Trans. Signal Processing, 41(12):3445~3462. Said A. and Pearlman W. A. (1996), A new, fast, and efficient image codec based on set partitioning in hierarchical trees, IEEE Trans. Circuits Syst. Video Technol. ,vol.6,pp.243-250. Daubechies, I. (1988), Orthonormal bases of compactly supported wavelets, Communications on Pure and Applied mathematics, Vol. 41, No. 11, pp.909-996. Pearlman, W. A., Islam, A., Nagaraj, N., and Said, A., Efficient, low-complexity image coding with a set-partitioning embedded block coder, http://www.cipr.rpi.edu/~pearlman/papers/csvt02_pins.pdf. Quegan,S. (1990), Interpolation and sampling in SAR images, IEEE Trans. On Geoscience and remote sensing vol28,641-646 Zeng Z., and Jan G. C. (2001), SAR image data compression using a tree-structured wavelet transform[J] IEEE Trans. Geoscience and Remote Sensing, 39(3): 546 ~552 Sang, H., Guo H., Wang C., and Han C. (2004), A SAR image filtering method based on wavelet transform, Bulletin of Surveying and Mapping, in print.