GISdevelopment.net ---> AARS ---> ACRS 2004 ---> Data Processing: Image Classification A Distributed Non-Parametric Unsupervised Classification Algorithm for Remotely Sensed Optical Imagery B. Liu, T. Bretschneider School of Computer Engineering, Nanyang Technological University N4-02a-32 Nanyang Avenue, Singapore 639798 Tel: +65 – 6790 6045, Fax: +65 – 6792 6559 SINGAPORE Email: astimo@ntu.edu.sg ABSTRACT: The previously proposed mean-shift algorithm provides a simple and non-parametric technique for estimating density gradients, which was generalised to image classification and segmentation. This paper proposes two extensions to the algorithm, namely an approach to improve the classification accuracy and the implementation for parallel / distributed computer architectures. The first issue is addressed by handling the overlapping of ground cover classes in the spectral space by incorporating the spatial information, while a parallelisation was developed for the latter issue. 1. INTRODUCTION The previously proposed mean-shift (MS) algorithm provides a simple and non-parametric tech-nique for estimating density gradients, which was generalised to image classification and segmentation (Comaniciu, 2002). It is a partitioning clustering technique augmented by analys-ing a complex multimodal feature space to delineate arbitrarily shaped clusters in it. Unlike other approaches this method does not assume any probability density function in advance and thus is well suited for the application in unsupervised classification with a wide range of possi-ble input scenes. This is of foremost importance for the targeted platform, i.e. the on-board execution on the mini-satellite X-Sat (Bretschneider, 2004). Moreover, the algorithm exhibits an almost linear time complexity and thus is advantageous for the fulfilment of the realtime processing requirements of the mission. This paper proposes two extensions to the MS algo-rithm, namely an approach to improve the classification accuracy and the implementation for the parallel computer architectures of the X-Sat. The emphasis is on a fast and stable classification algorithm rather than on high precision for a selected number of test scenes since the result is used as a selection criterion for scenes to be processed further. The analysis of the developed technique presents the obtained speedup factors by the parallelisation and investigates the in-creased classification accuracy. 2. DISTRIBUTED MEAN-SHIFT CLUSTERING ALGORITHM 2.1. Introduction of the Mean-Shift Algorithm This part reviews the basic theory of the MS algorithm according to Comaniciu (1997). Assume that the probability density function P(x) of the feature vector x is unimodal. Feature vec-tors y are defined as all the feature vectors which are lying in a sphere Sx of radius r, centred at x with ||y–x||<r. 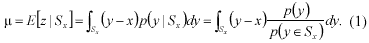Then, the expected value of the vector z=y–x is since the first term vanishes. 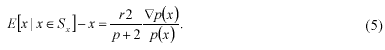Hence: The left side of Equation (5) is called the mean-shift vector. It has three important properties: Firstly, the mean-shift vector is small for regions which have a large p(x) and a small Ñp(x) and large for regions which have a low p(x). Secondly, the direction of the mean-shift vector corre- sponds to the gradient direction of the probability density function. Thirdly, at the mode, which corresponds to the maximal of the probability density function, the mean-shift vector is zero. The first two properties can be used to develop a gradient based search methods for the modes during non-parametric clustering because the mean-shift vector can be viewed as an estimation of the gradient of the probability density function. The last property guarantees the convergence of the iterative algorithm, i.e. the locating of modes (the centres of the regions of high concentration) of multi-dimensional data sets. At the first step given a radiush for the search window, the algorithm computes the mean-shift vector according to Equation (5) within the search window located at position m. Afterwards, the algorithm deletes all the items (data points) in the search window every time a new mode is found. At last the whole process stops if the number of the remaining items is less than a preset threshold. 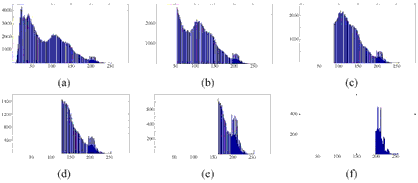Figure 1: Iterative finding of modes by the MS algorithm Although the nature of the utilised multispectral data in this investigation is multi-dimensional, a one-dimensional data set described by the corresponding histogram is used for demonstration purposes. Starting with the initial histogram shown in Figure 1(a), the initial location m is the origin. Hence, the search window is defined for the interval [0…h] and the algorithm begins to search for modes in this window. If a mode is found, the corresponding histogram bins are de-leted and the location m moved by h units to the right. This iteration is repeated until conver-gence is achieved. It is worthwhile mentioning that the results for reasonable choices of h are fairly stable. This investigation used an empirically estimated radius with h=40. For a com-pletely unsupervised approach it is assumed to test various radiuses and select one result with respect to the number of expected and detected ground cover types. 2.2. Majority Voting Filter The original version of the MS algorithm solely considers the contained spectral information and neglects any available spatial knowledge of the underlying data. For example two Gaussian distributed clusters in the two-dimensional feature space intersect each other like shown in Figure 2 but are separated in the actual scene. 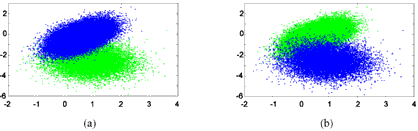Figure 2: Test data set shown from different view points (65536 data points) To measure the overlap rate of two clusters the spheres with radius 2s (representing more than 95% of the data points) are considered. Then, a point is regarded to be part of the overlap if its distances to both cluster means are less than 2s. Hence, the overlap rate is defined as (No/Na)´100% with No being the number of the points in the overlapped area and Na being the total number of points in the data set. Applying the MS algorithm with h=40 directly to the data set, the algorithm finds the two clusters correctly. However, 2437 points (3.72%) are misclassi- fies which can be seen conceptually from Figure 3. Note that this misclassification was achieved in a noise free simulation. Thus, the misclassification rate for actual data is higher. 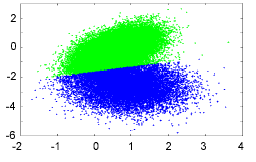Figure 3: Result of MS algorithm To handle the overlapping area of clusters in the feature space and therefore to improve the classification accuracy, the majority voting filter (MVF) is introduced which utilises the neighbourhood information in the classification map to handle the overlapping problem. In the classification map, a cluster index is assigned to every pixel. Then the MVF performs a local consistency check within the proximity of each pixel and changes its cluster association if the original assignment diverges too significantly. The basic motivation is that ground covers are spatially separated to a large extend. Figure 4 shows the classification result for the data in Figure 2 (extended by spatial information) in the two-dimensional space using a local environ-ment of 3´3 pixels. As a result only 24 out of 65536 pixels are misclassified. Obviously, for actual data the approach results in the elimination of smaller regions. However, this is tolerable with respect to the highlighted objectives in Section 1. 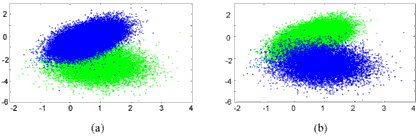Figure 4: Classification result with MVF applied 2.3. Distributed Mean-Shift Algorithm From the modified MS algorithm described in the previous sub-section, it can be concluded that a significant part of computational power is required in the post-processing step, i.e. the linear time complexity is lost. To improve the processing speed the raw satellite scene is partitioned into image strips according to the number of available processing nodes (PN) in the X-Sat com- pute payload PPU (Bretschneider, 2004). During the distribution of the image data to the individual nodes the histogram is created in the central field programmable gate arrays (FPGA) of the PPU and broadcasted to all participating PNs. The modes are clearly defined through the histogram and the creation of the cluster indices for each image pixel can be performed based on the minimum distances. The final step of applying the MVF is executed independently in each node. 3. RESULTS AND EVALUATION The first experiment was carried out for nine data sets containing each two overlapping Gaus- sian distributed clusters. Figure 5 shows the results, whereby the x-axis shows the overlapping rate, while the y-axis depicts the classification accuracy. The blue curve describes the classifica- tion accuracy of the MS algorithm, while the red curve consistently shows better results in terms of classification accuracy for the additional MVF step. 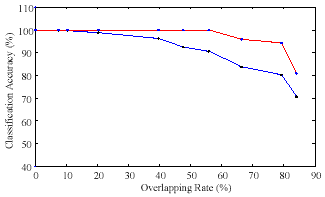Figure 5: Plot of classification accuracy Figure 6 compares the results of the EISMC approach (Liu, 2003) and the MS algorithm with MVF step (window size of 3´3 pixels for consistency check). Note that both techniques were developed for the same architecture under the identical mission requirements. Column (a) shows the respective raw sub-scenes, column (b) presents the results of the EISMC procedure (four clusters were found), and column (c) depicts the results of the modified MS technique (six clus-ters found). In general the EISMC keeps more details than the MS procedure due to the missing post-processing consistency check. Hence, in some cases edge information is lost. However, the main advantage of the MS with MVF is the realtime capability with respect to the acquisition speed of 81Mbit/s. 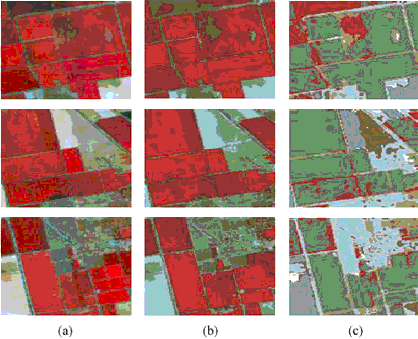Figure 6: Comparison of classification results: (a) original data, (b) EISMC, (c) MS with MVF Finally, Figure 7 shows the speedup graph of the distributed MS algorithm. This experiment was carried on a three band satellite image with the size of 3000´3000 pixels, and from the graph a speedup as large as seven was gained if nine processors were used. 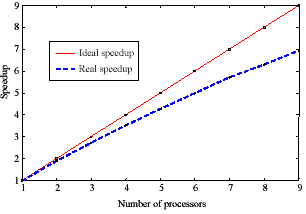Figure 7: D-Mean-Shift speedup graph 4. CONCLUSIONS The aim of providing a realtime capable classification algorithm for the parallel processing unit of the X-Sat was achieved. Two extensions to the original mean-shift algorithm were proposed in this paper, namely an approach to improve the classification accuracy and the implementation for a parallel / distributed computer architecture. REFERENCES Bretschneider, T., 2003. Singapore’s satellite mission X-Sat. Proceedings of the International Academy of Astronautics Symposium on Small Satellites for Earth Observation, Berlin, Ger- many, pp. 105–108. Bretschneider, T., Ramesh, B., Gupta, V., and McLoughlin, I. 2004. Low-cost space-borne processing on a reconfigurable parallel architecture. Proceedings of the International Conference on Engineering of Reconfigurable Systems and Algorithms, Las Vegas, USA, pp. 93–99. Comaniciu, D., and Meer, P., 1997. Robust analysis of feature spaces: Color image segmenta- tion. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, pp. 750–755. Comaniciu, D., and Meer, P., 2002, Mean shift: A robust approach toward feature space analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, pp. 603–619. Liu, B., and Bretschneider, T., 2003, D-ISMC: A distributed unsupervised classification algo- rithm for optical satellite imagery. Proceedings of the IEEE International Geoscience and Re- mote Sensing Symposium, Toulouse, France, 6, pp. 3413–3415.