Land Use classification using satellite data for stormwater management

Land Use classification using satellite data for stormwater management

Lourdes V. Abellera 1 and Michael K. Stenstrom 2
1 Graduate Student and 2 Professor,
Department of Civil and Environmental Engineering
University of California, Los Angeles, California 90095-1593, USA
Tel: 1-310-825 1346; Fax: 1-310-206 2222
Email: labeller@ucla.edu

ABSTRACT
Land use is an important input parameter for stormwater models. It is used to calculate surface imperviousness, which determines runoff rates and volumes. The type of land use is also associated with the kind and amount of pollutants generated in a parcel of land. Many projects still utilize the traditional ways of delineating land uses such as photo-interpretation and field surveys. By using satellite data, scientists have attempted to increase the efficiency and accuracy of the land use classification process. Statistical classifiers, such as the parallelepiped, minimum distance to means, maximum likelihood, and clustering algorithms were the first classifiers to be developed. Recently, scientists have incorporated ancillary data in the classification, usually employing geographic information systems (GIS). They have also developed contextual and fuzzy classifiers. Furthermore, they have applied artificial intelligence techniques such as neural networks and knowledge-based systems. However, only a few studies are related to stormwater management. As the conventional methods of delineating land uses are time-consuming and labor-intensive, more engineers and planners should consider utilizing satellite data to provide inputs to their stormwater models. In this endeavor, some of the factors to consider are the level of classification detail, relevant land use categories, and methods to assess accuracy.

INTRODUCTION
The goal of stormwater management is to control runoff quantity and maintain water quality. Elevated volumes and flow rates of runoff can have a number of harmful effects including flooding, stream erosion, and habitat destruction. Surface runoff can also carry and distribute sediment, nutrients, oxygen-demanding organics, toxic substances, and pathogens to drainage systems and watercourses. These pollutants may also threaten aquifers. Engineers and planners are making use of stormwater models to provide solutions to these problems. A stormwater model simulates the movement of stormwater and transported materials through a watershed (Nix, 1994). However, modelers find that data input and parameter acquisition is a laborious process. This is because stormwater runoff is a poorly-understood environmental system. Innumerable factors affect runoff including topography, precipitation characteristics, and human activities. Also, the large area that needs to be quantified makes data collection using conventional methods too time-consuming and expensive.

Land use is a necessary input parameter for stormwater models. It is used to estimate the imperviousness of surface areas. Each type of land parcel is impervious to rainfall to some extent. Commercial business districts, for instance, are highly impervious because most of the land surface is paved or has structures on it. Open land, on the other hand, has very little impervious surface, and water will directly infiltrate the ground. Therefore, more runoff will be generated in a land parcel that has more impervious surface. The category of land use also determines the nature and quantity of pollutants produced by a parcel of land. For example, oil and grease concentrations were higher in runoff from commercial properties and parking areas than in residential areas (Stenstrom et al., 1984).

Generally, land use categories are manually delineated from aerial photographs and field work data. However, land use classifications can be obtained more efficiently by digital processing of satellite imagery. Compared to aerial photos, satellite data are generally faster and less expensive to acquire and interpret. Since satellite images are captured on a regular basis, a time series of data from a given area are readily obtainable. They are available in almost all parts of the world in different resolutions (e.g., 30 meters for Landsat, 20 meters for SPOT) and in various operating modes (e.g., Thematic Mapper, Synthetic Aperture Radar). Because of their digital format, they can be directly investigated with numerous image processing software programs. They can be processed to be included in a geographic database. They are also compatible with several hydrologic modeling software packages that are GIS-based.

Remote sensing scientists often interchange the terms “land use” and “land cover”. Their denotations, however, are distinct. Land cover is the physical material present on the surface of a land parcel (e.g., grass, water). Land use, on the other hand, refers to the human activity associated with that land parcel (e.g., residential, industrial). Both land cover (physical component of the land parcel) and land use (economic component) data are important for stormwater modeling. The results of modeling aid in the selection of best management practices. The standard classifiers utilized in land use classification are statistical in nature. In Figure 1, the black dots in the scatterplot represent a subset of pixels in a satellite image. They are plotted according to their digital numbers (DN) in Band 1 (x-axis) and Band 2 (y-axis). Pixels of the same class exhibit a natural centralizing tendency. In the parallelepiped classification strategy, the classes are “enclosed” by a box or a parallelepiped in multidimensional space (Class 1 in Figure 1). These parallelepipeds are specified by the sets of DNs defining a class. In the minimum distance to means classifier, the statistical descriptor is the set of the average spectral values in the bands considered. This is also called the mean vector for each class (the diamond mark in Class 2 in Figure 1). The Euclidean distance between the value of the unknown pixel and a class mean vector is computed. The unknown pixel is assigned to that class nearest to that pixel. In the maximum likelihood classification, the mean vector and the covariance matrix are computed for each class. The covariance matrix is a way to represent the spread of the data (Class 2 has more variability than Class 1). With these two parameters, the statistical probability of a pixel being a member of a specific land cover type can be calculated (Lillesand and Kiefer, 1994). In clustering, the algorithm finds the natural spectral groupings of pixels. The procedure is similar to the minimum distance to means classifier except that the mean vector migrates (Richards, 1986). All these classifiers have drawbacks. For example, in the maximum likelihood classifier, if the pixels are characterized by non-normality, then this classifier will not work well. Computation also takes a long time (ERDAS Field Guide, 1997).

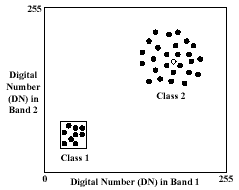
Figure 1: Pixel observations in a scatterplot
LAND USE CLASSIFICATION: NEW APPROACHES
As the traditional classifiers have limitations that reduce the correctness of land use/cover classification, researchers were inspired to devise new strategies to improve the classification process. To determine the performance of their proposed approach, investigators compare their methods with these standard classifiers. In particular, the maximum likelihood classifier is the most widely analyzed because of its well-developed theoretical base, facility of automation, and reliable tracking record (Richards, 1986; Lillesand and Kiefer, 1994). Many have utilized the confusion matrix for accuracy assessment and the common measures derived from it (e.g., overall accuracy), but other metrics are also available. For example, Cohen’s kappa coefficient is often employed to accommodate for the effects of chance that a pixel has been classified into its correct land cover category (Foody, 2002). There are many ways that researchers try to refine the accuracy of classification. Only a small fraction of these are explored here.

Incorporation of Ancillary Data
Ancillary data, usually in GIS format, can be incorporated before, during, and after classification (Hutchinson, 1982). These are called stratification, classifier operations, and post-classification sorting, respectively. In stratification, the image is divided into smaller regions to enhance data homogeneity. Then, relevant properties of the land use classes are derived. For instance, the image may be segmented based on the density of the built-up areas (Michalak, 1993). In classifier operations, the decision rules of the statistical classifiers are adjusted to reflect the areal combination of the known land use classes by specifying prior probabilities (McIver and Friedl, 2002). Another technique is to treat the ancillary data as another band in the classification. Elumnoh and Shrestha (2000) combined a digital elevation model with the spectral bands using Iterative Self-Organizing Data Analysis. In post-classification sorting, similar land use classes with different spectral responses are merged based on the ancillary data. Harris and Ventura (1995) used zoning and housing density data to correct regions of confusion.

Contextual Classifiers
The standard classification strategies are point or pixel specific classifiers. Here, the pixels are classified independently of the classifications of the neighboring pixels. It has long been acknowledged that adjacent pixels may have similar land cover classes. Contextual classification is employed when neighboring pixels are taken into account (Richards, 1986). Barnsley and Barr (1996) developed a two-stage classification system, the first of which involved the standard per-pixel classification of the image into broad land cover classes. In the second stage, they passed a kernel across the image which took into account both the frequency and the spatial arrangement of the pixels. Wharton (1982) recognized that urban land use classes have different amounts of the same land cover components. For example, there are more pavement and roof components in a commercial district than in a single-family residential area. This observation was his basis for his two-stage cluster analysis procedure.

Neural Networks
A neural network is an information system of interconnected elements called neurons (Awad, 1996). In Figure 2, neurons measure the inputs, calculate their weights, total the weighted inputs, and compare this value to a threshold. If this value is larger than the threshold, the neurons fire (output). Otherwise, it produces no signal. When the network alters the weights and changes its activity based on the inputs, learning has taken place. Back propagation involves adjusting the weights by backing up from the output. In a neural network, the inputs are the individual digital numbers. Ancillary data can also be added to the pattern of the pixels. The outputs are the land use/land cover categories of the pixels. Lee (2003) utilized not only the spectral characteristics of the image, but also included the pixel locations as inputs to his neural networks. Sometimes, the number of nodes can be huge. Kanellopoulos et al., (1992) trained a 98-node network to identify 20 land cover classes.

Inputs Outputs

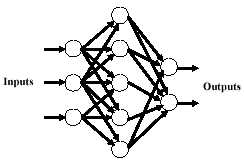
Figure 2: An example of a neural network
Fuzzy Classifiers
So far, we have discussed only per-pixel classification, in which a pixel can only have one and only one category. These are called hard classifiers. In urban regions, a pixel in reality may have more than one category because of the heterogeneity of the land cover composing that pixel. We call this a mixed pixel. Presence of these pixels in an urban setting prompted the development of soft or fuzzy classifiers. This term stems from the fact that a pixel does not belong fully to one class but it has different degrees of membership in several classes. The mixed pixel problem is more pronounced in lower resolution data. In fuzzy classification, or pixel unmixing, the proportion of the land cover classes from a mixed pixel is calculated (Eastman and Laney, 2002). Fuzzy classifiers are especially applicable if areas of individual categories are needed, for example, the total area of impervious surface in a watershed. Wang (1990) devised an algorithm similar to maximum likelihood except that he replaced the mean vectors and the covariance matrix with their fuzzy equivalents.

Knowledge-Based Systems
A knowledge-based system performs a task by applying rules of thumb, called heuristics, to a symbolic representation of knowledge, instead of using mostly statistical (e.g., maximum likelihood) or algorithmic (e.g., neural network) methods. It is sometimes regarded to be synonymous to an expert system. Here, thematic or geometric data are included in the classification process. This is done when it is difficult or insufficient to recognize classes only on the basis of spectral characteristics. This approach must acquire knowledge about the relationships between classes and the various ancillary sources (Skidmore, 1989). One group called hierarchical techniques eliminates alternative hypotheses during inference until only one hypothesis is left. Conceptually, land-cover categories are represented as leaves of bi- or multinary trees, with decision rules applied at each node to stop or continue on a decision course (Figure 3). Johnsson and Kanonier (1991) segmented a classified image based on their spectral properties. Then, they calculated the size, perimeter, and shape of the segments. In effect, their rules were based both on spectral and spatial properties of the image.

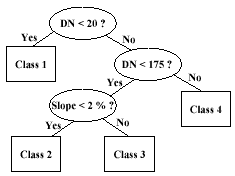
Figure 3: An example of a decision tree
DISCUSSION
Numerous scientists in different disciplines (e.g., geography, computer science, electrical engineering) have exerted much effort to improve the land use classification process. However, the ultimate goal of many of these investigations is the classification procedure itself. There are some studies that analyzed satellite data specifically to provide inputs to their stormwater models. Examples that extracted mainly land use classes are investigations by Cermak et al. (1979), Ragan and Jackson (1980), and Harris and Ventura (1995). More engineers and planners should consider utilizing satellite data for their stormwater modeling efforts. However, there are issues to be addressed. First, the level of detail must be appropriate for a specific study area. For example, some land use classification studies can identify up to Anderson level III. However, in stormwater modeling, Anderson level II is often sufficient even for a highly urbanized city like Los Angeles. The level of detail is also associated with the ground resolution of the satellite data. For instance, a high resolution IKONOS image will definitely resolve more objects. A decision should be made if the accuracy achievable is indeed necessary because using this image has disadvantages such as expense and large storage space. Second, the categories of land use must be relevant to the study area. For example, “transportation” may be a relevant land use category in Los Angeles where wide freeways are prevalent, but it may not be a useful land use class in a small city in Kansas. Lastly, the performance of the classification procedure should be assessed. One way is to apply the accuracy assessment tool (i.e. error/confusion matrix) of the remote sensing community. But we can also evaluate the results of the stormwater modeling itself. The modeling outputs can be runoff volumes, hydrographs, or pollutant loadings. We can compare the outputs that used satellite data to those that utilized traditional methods (e.g., stream gauging). By addressing these issues, satellite data can be applied in stormwater management in the best possible way.

ACKNOWLEDGMENT
This paper was written in connection with the main author’s Ph.D. dissertation, which was funded by the Philippine government through the Department of Science and Technology.

REFERENCES

Awad, E.M., 1996. Building Expert Systems Principles, Procedures, and Applications. West Publishing Company, St. Paul, Minnesota, pp. 427-454.
Barnsley, M.J. and Barr, S.L., 1996. Inferring urban land use from satellite sensor images using kernel-based spatial reclassification. Photogrammetric Engineering and Remote Sensing, 62 (8), pp. 949-958.
Cermak, R.J., Feldman, A. and Webb, R.P., 1979. Hydrologic land use classification using Landsat. In: Satellite Hydrology, edited by Deutsch, M., Wiesnet, D.R. and Rango, A., American Water Resources Association, Minneapolis, Minnesota, pp. 262-269.
Eastman, J.R. and Laney, R.M., 2002. Bayesian soft classification for sub-pixel analysis: A critical evaluation. Photogrammetric Engineering and Remote Sensing, 68 (11), pp. 1149-1154.
Elumnoh, A. and Shrestah, R.P., 2000. Application of DEM data to Landsat image classification: Evaluation in a tropical wet-dry landscape of Thailand. Photogrammetric Engineering and Remote Sensing, 66 (3), pp. 297-304.
ERDAS Field Guide, 4th Edition, 1997. Erdas, Inc., Atlanta, Georgia, pp. 213-258.
Foody, G.M., 2002. Status of land cover classification accuracy assessment. Remote Sensing of Environment, 80 (1), pp. 185-201.
Harris, P.M. and Ventura, S.J., 1995. The integration of geographic data with remotely sensed imagery to improve classification in an urban area. Photogrammetric Engineering and Remote Sensing, 61 (8), pp. 993-998.
Hutchinson, C.F., 1982. Techniques for combining Landsat and ancillary data for digital classification improvement. Photogrammetric Engineering and Remote Sensing, 48, pp. 123-130.
Johnsson, K. and Kanonier, J., 1991. Knowledge based land-use classification. In: Proceedings International Geoscience and Remote Sensing Symposium IGARSS ’91, 3- 6 June, 1991, Espoo, Finland, pp. 1847-1850.
Kanellopoulos, I., Varfis, A., Wilkinson, G.G. and Megier, J., 1992. Land-cover discrimination in SPOT HRV imagery using an artificial neural network- A 20-class experiment. International Journal of Remote Sensing, 13 (5), pp. 917-924.
Lee, H.H., 2003. Data mining of remote sensed data for stormwater systems. Ph.D. Dissertation, University of California, Los Angeles, USA, pp. 1-158.
Lillesand, T.M. and Kiefer, R.W., 1994. Remote Sensing and Image Interpretation, 3rd Edition. John Wiley & Sons, Inc., USA, pp. 524-647.
McIver, D.K. and Friedl, M.A., 2002. Using prior probabilities in decision-tree classification of remotely sensed data. Remote Sensing of Environment, 81, pp. 253-261.
Michalak, W.Z., 1993. GIS in land use change analysis: Integration of remotely sensed data into GIS. Applied Geography, 13, pp. 28-44.
Nix, S.J., 1994. Urban Stormwater Modeling and Simulation. Lewis Publishers, Boca Raton, Florida, pp. 1-13.
Ragan, R.M. and Jackson, T.J, 1980. Runoff synthesis using Landsat and SCS model. Journal of the Hydraulics Division, Proceedings of the American Society of Civil Engineers, 106 (HY5), pp. 667-678.
Richards, J.A., 1986. Remote Sensing Digital Image Analysis: An Introduction. Springer-Verlag, Berlin, Heidelberg, Germany, pp. 173-205.
Skidmore, A.K., 1989. An expert system classifies eucalypt forest types using Thematic Mapper data and a digital terrain model. Photogrammetric Engineering and Remote Sensing, 55 (1), pp. 133-146.
Stenstrom, M.K., Silverman, G.S. and Bursztynsky, T.A., 1984. Oil and grease in urban stormwaters. Journal of Environmental Engineering, 110 (1), pp. 58-72.
Wang, F., 1990. Fuzzy supervised classification of remote sensing images. International Transactions on Geoscience and Remote Sensing, 28 (2), pp. 194-201.
Wharton, S.W., 1982. A contextual classification method for recognizing land use patterns in high resolution remotely sensed data. Pattern Recognition, 15 (4), pp. 317- 324.